1. Quadripôle

1.1. Problème énergétique

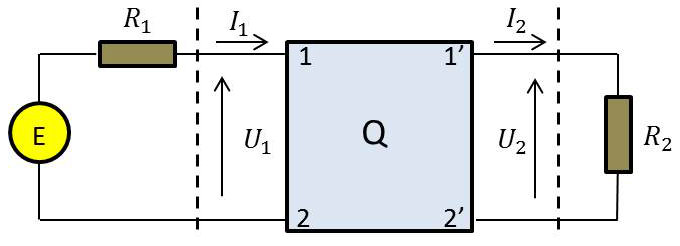Nous considérons le filtre comme un quadripôle dont les bornes d’entrée \((1,~1')\) sont fermées sur un générateur de fém \(E\) et de résistance interne \(R_1\) et dont les bornes de sortie \((2,~2')\) sont fermées sur une charge \(R_2\) assimilée à une résistance dans la majorité des cas.

Nous avons déjà fait remarquer que le filtre passif, composé d’inductances et de capacités, puisait toute son énergie dans la source \(E\) avec une certaine dégradation si les composants présentent des pertes (généralement faibles).

1.2. Théorie de l’insertion

Le filtre doit fonctionner dans les conditions d’adaptation (résistance interne \(R_1\) du générateur et résistance de charge \(R_2\)). On se rappellera à cet effet les formules classiques du montage potentiomètre \((R_1,~R_2)\), sachant que c’est ce montage que l’on retrouve à partir du moment où le filtre a été enlevé entre le générateur et la charge.

La puissance dissipée dans la charge \(R_2\) est : \[P_2=\frac{|V_2|^2}{R_2}\]

La puissance maximale que le générateur peut dissiper dans la charge, en l’absence du filtre (adaptation \(R_2=R_1\)), est : \[P_{2~max}=\frac{|V_1|^2}{4}~\frac{1}{R_1}\]

1.2.1. Matrice chaîne

La matrice chaîne est encore appelée matrice de transfert ou de transmission. On pourra écrire : \[\begin{pmatrix} V_1\\ I_1 \end{pmatrix} = \begin{pmatrix} A& &B\\ C& &D \end{pmatrix} \times \begin{pmatrix} V_2\\ I_2 \end{pmatrix}\]

Il est intuitif que, pour une cascade de quadripôle insérée entre les deux résistances, la matrice chaîne de l’ensemble est le produit (non commutatif) des matrices élémentaires composantes. C’est la matrice qui sera le plus couramment utilisée pour les problèmes d’analyse et de synthèse des filtres.

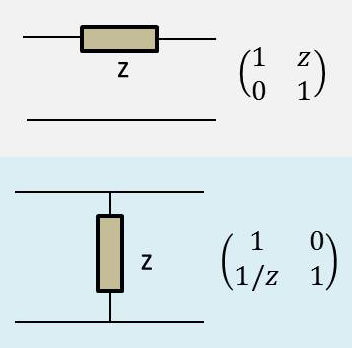Les deux matrices de base (matrice dite série pour la première et matrice dite parallèle pour la deuxième) sont également représentées ci-contre.

Le filtre passif se présente comme une structure dite en échelle, c’est-à-dire alternativement avec un bras en série et un bras en parallèle, chacun d’eux comprenant un ou plusieurs composants (L ou C) ou (L et C). Pour obtenir la matrice de transfert du filtre, il suffit de composer les matrices équivalentes de chacun de ses composants.

1.2.2. Matrice chaîne et atténuation

La connaissance des éléments de la matrice chaîne permet de calculer l’atténuation du filtre en fonction de la fréquence. L’atténuation du quadripôle est définie par : \[A_{dB}=10~\log_{10}\frac{P_{2~max}}{P_2}\]

Et on démontre que : \[\frac{P_{2~max}}{P_2}=\frac{R_2}{4~R_1}~\Big|C+\frac{A}{R_1}+\frac{B}{R_1~R_2}+\frac{D}{R_2}\Big|^2\]

L’expression complexe \((C+A/R_1+B/R_1~R_2+D/R_2)\) correspond à la fonction de transfert \(H(p)\) exprimée avec les éléments du circuits disposés dans leurs matrices respectives. On peut donc en déduire le gain du filtre (valeur absolue), donc l’atténuation et la phase par l’argument de ce nombre complexe.

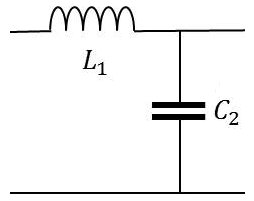Exemple d’un filtre polynômial passe-bas d’ordre 2 : \[\begin{pmatrix} A& &B\\ C& &D \end{pmatrix} = \begin{pmatrix} 1& &j~L_1~\omega\\ 0& &1 \end{pmatrix} \times \begin{pmatrix} 1& &0\\ j~C_2~\omega& &1 \end{pmatrix}\]

Ce qui donne : \[\begin{pmatrix} A& &B\\ C& &D \end{pmatrix} = \begin{pmatrix} 1-L_1~C_2~\omega^2& &j~L_1~\omega\\ j~C_2~\omega& &1 \end{pmatrix}\]

L’analyse consiste donc à écrire chaque matrice chaine \(A_i,B_i,C_i,D_i\) et en faire le produit pour obtenir la matrice chaine de l’ensemble, ayant bien présent à l’esprit que la commutation est impossible.

D’où l’atténuation, la phase et éventuellement le temps de propagation de groupe :

\[\begin{aligned} A_{dB}(f)&=10~\log_{10}~\Big|C+\frac{A}{R_1}+\frac{B}{R_1R_2}+\frac{D}{R_2}\Big|^2\\ \varphi(f)&=\arg\Big(C+\frac{A}{R_1}+\frac{B}{R_1~R_2}+\frac{D}{R_2}\Big)\\ \tau(f)&=2\pi~\frac{d\varphi}{d\omega}\end{aligned}\]

2. Principe fondamental de synthèse

On se place toujours dans l’hypothèse du filtre passe-bas large bande.

2.1. Raisonnement du dipôle passif

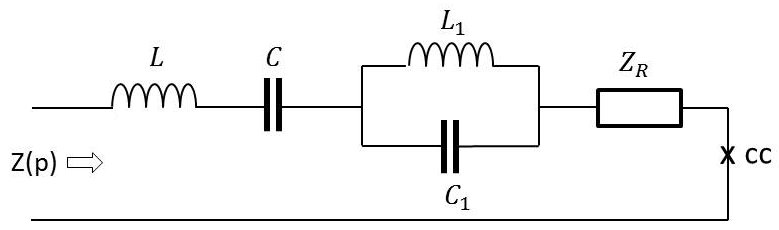Considérons le dipôle réactif représenté ci-contre. Il peut être considéré comme un quadripôle dans lequel la borne de sortie a été mise en court-cicuit (\(cc\)).

\(Z_R\) représente une suite d’impédances analogues à celles qui la précèdent.

La fréquence du circuit bouchon est donnée par : \[\omega_1^2=\frac{1}{L_1~C_1}\]

L’impédance \(Z(p)\), vue des bornes d’entrée a pour expression : \[Z(p)=Lp+\frac{1}{Cp}+\frac{\cfrac{1}{C_1}~p}{p^2+\omega^2}+Z_R\]

Ce schéma va nous permettre de comprendre que les valeurs des éléments du circuit peuvent être déduits de l’expression analytique de \(Z(p)\) à partir d’une technique d’extraction des résidus de cette fonction. Bien que simple (voire intuitive), il n’est pas de méthode plus générale.

On voit immédiatement que :

\[\begin{aligned} &L=\frac{Z(p)}{p}~|~_{p\rightarrow\infty}\\ &\frac{1}{C}=p~Z(p)~|~_{p=0}\\ &\frac{1}{C_1}=\frac{(p^2+\omega_1^2)~Z(p)}{p}~|~_{p^2=-\omega_1^2}\end{aligned}\]

Renouant avec une technique d’intégration pour les fonctions complexes (voir les séries de Laurent), on a tout simplement procédé à l’extraction du résidu à l’infini, du résidu à l’origine et du résidu fini en \(p=j\omega\), mais cette fois en direct, sans dérivation.

Il est évident que ces extractions ne sont possibles que si la fonction \(Z(p)\) (et par voie de conséquence la fonction \(H(p)\) dont elle est issue) obéit à un certain nombre de contraintes. Nous ne les aborderons pas ici et les supposerons pour l’instant réalisées.

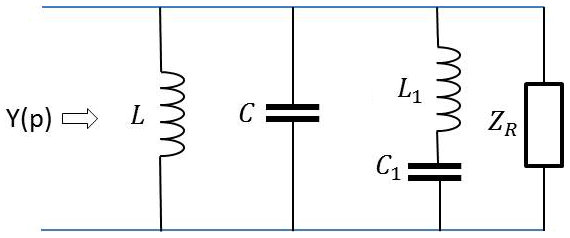Notons que nous aurions pu adopter le même raisonnement sur le dipôle associé pour lequel c’est la fonction admittance qui est mise à contribution : \[Y(p)=Cp+\frac{1}{Lp}+\frac{\cfrac{1}{C_1}~p}{p^2+\omega^2}+Y_R\]

Ces deux images symboliques laissent pressentir le mécanisme de synthèse le plus général, donc sur un quadripôle non particulier (branches en parallèle et branches en séries) : une alternance de traitement en \(Z(p)\) et \(Y(p)\).

2.2. Synthèse d’un filtre passe-bas polynomial

Un filtre passe-bas en échelle n’est constitué que d’inductances et de capacités (donc ni \(L~C\) en série, ni \(L~C\) en bouchon). Il existe alors une méthode qui reprend le principe exposé dans le dipôle, mais sous une forme automatique et algorithmique. C’est ce que l’on appelle la technique d’extraction continue par fractions.

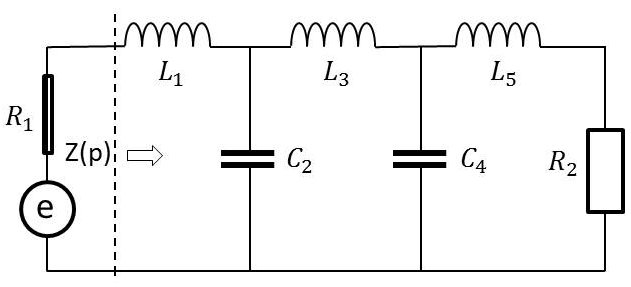Pour fixer les idées, la structure ci-contre est celle d’un filtre polynômial d’ordre 5.

On rencontre généralement une expression de la forme : \[\frac{Z(p)}{R_1}=p~\frac{A(p^2)}{B(p^2)}\]

\(R_1\) : résistance interne du générateur

Par la seule division des polynômes, on obtient directement les valeurs des composants. Cette division se présente sous la forme (cas du filtre d’ordre 5) : \[\frac{Z(p)}{R_1}=p~L_1+\cfrac{1}{p~C_2+\cfrac{1}{p~C_2+\cfrac{1}{p~L_3+\frac{1}{p~C_4+\cfrac{1}{p~L_5+\cfrac{1}{R_2}}}}}}\]

Remarque

Les valeurs des composants sont des valeurs normalisées par rapport à la fréquence de référence mais également par rapport à \(R_1\) explicitement associé à \(Z(p)\). Il faudra prendre en compte ces deux éléments au moment de la dénormalisation (valeurs physiques des composants).

Exercice

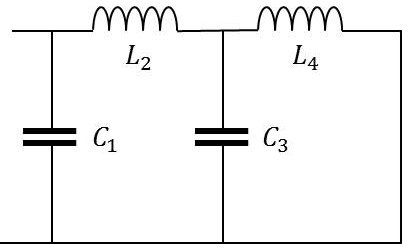On considère le filtre ci-contre d’ordre 4 dans lequel la sortie est en court-circuit.

Son impédance vue de l’entrée et son admittance vue de l’entrée (doublement normalisées) ont pour expressions :

\[\begin{aligned} &Z(p)=\frac{p^3+p}{p^4+10~p^2+9}\\ &~\\ &Y(p)=\frac{p^4+10~p^2+9}{p^3+p}\end{aligned}\]

En effectuant les divisions, on obtient successivement:

\[\begin{aligned} &(p^4+10~p^2+9)~/~(p^3+p)=p &&R~:~6~p^2+9 &&C_1=1\\ &(p^3+p)~/~(6~p^2+9)=\frac{1}{6}~p &&R~:~\frac{5}{2}~p &&L_2=\frac{1}{6}\\ &(6~p^2+9)~/~\Big(\frac{5}{2}~p\Big)=\frac{12}{5}~p &&R~:~9 &&C_3=\frac{12}{5}\\ &\Big(\frac{12}{5}~p\Big)~/~9=\frac{5}{18}~p &&R~:~0 &&L_4=\frac{5}{18}\end{aligned}\]

Remarque : Les valeurs affichées des composants sont normalisées (sans dimension).

3. Dénormalisations et filtres non passe-bas

3.1. Filtre original passe-bas

Si le filtre a été synthétisé à partir d’une fonction de transfert connue par ses coefficients réels, les valeurs obtenues pour les inductances et les capacités sont des valeurs à dimensions physiques, donc directement utilisables.

Ce cas se présente rarement et le filtre est généralement synthétisé à partir de la fonction de transfert, fraîchement calculée, donc normalisée. Entrent en jeu la fréquence ou pulsation de normalisation (\(\omega_0\)) et la résistance du générateur (\(R_1\)).

On écrira donc :

\[\begin{aligned} &L_n~\rightarrow~L=\frac{L_n~R_1}{\omega_0}\\ &C_n~\rightarrow~C=\frac{C_n}{R_1~\omega_0}\end{aligned}\]

3.2. Filtre prototype passe-bas

On rappelle que le gabarit passe-bas de synthèse est décliné du gabarit non passe-bas. On considère ici les cas du filtre passe-haut et du filtre passe-bande, la transformation de fréquence correspondant au filtre coupe-bande étant exactement l’inverse de celle du passe-bande.

3.2.1. Filtre original passe-haut

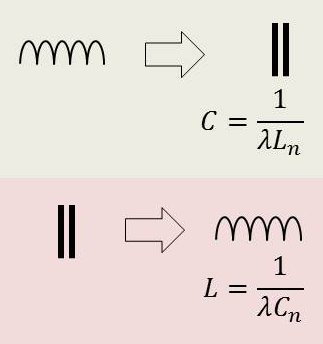On rappelle la formule de normalisation (transformation de fréquence) : \[p_n=\frac{\lambda}{p}\]

Du point de vue des impédances, on fera un échange \(L~\leftrightarrow~C\) :

\[\begin{aligned} &L~:~L_n~p_n=\frac{\lambda~L}{p}=\frac{1}{C~p}\quad;\quad~C=\frac{1}{\lambda~L_n}\\ &C~:~\frac{1}{C_n~p_n}=\frac{p}{\lambda~C_n}=L~p\quad;\quad~L=\frac{1}{\lambda~C_n}\end{aligned}\]

La dénormalisation doit être achevée par rapport à \(R_1\).

3.2.2. Filtre original passe-bande

On sait que la transformation est homographique : \[p_n=j~\Omega=\lambda~p+\frac{\mu}{p}\]

avec, dans le cas des filtres polynômiaux, par exemple :

\[\begin{aligned} &\lambda=\frac{1}{\Delta\omega}\quad;\quad \Delta\omega=\omega_p-\omega_{p'}\\ &\mu=\lambda~\omega_0^2\quad;\quad \omega_0^2=\omega_p~\omega_{p'}=\omega_a~\omega_{a'}\end{aligned}\]

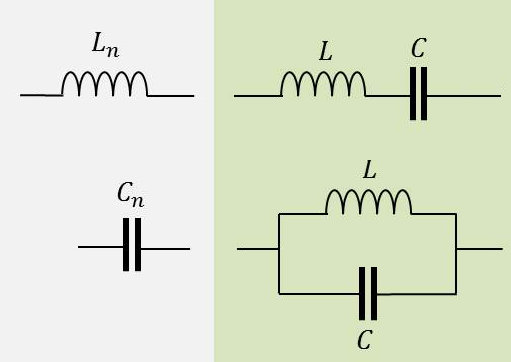L’inductance est transformée en circuit résonant LC série et la capacité en circuit résonnant parallèle, avec les correspondances suivantes :

\[\begin{aligned} &L~:~L_n~\rightarrow~L=\lambda~L_n\quad;\quad C=\frac{1}{\mu~L_n}\\ &C~:~C_n~\rightarrow~L=\frac{1}{\mu~C_n}\quad;\quad C=\lambda~C_n\\ &L~C=\frac{\lambda}{\mu}\quad\text{dans les deux cas (série et parallèle)}\end{aligned}\]

La dénormalisation doit être achevée par rapport à \(R_1\).

4. À l’horizon du filtre passif LC large bande

Tout ce qui vient d’être vu, ou plutôt entrevu, dirait le spécialiste, devrait donner une bonne idée des bases fondamentales de calcul. Ce qui vient d’être dit doit permettre de survoler des études connexes.

4.1. Filtre triplaque (HF)

Aux fréquences élevées, la réalisation des inductances devient problématique (dimensions). La technique du triplaque ou (microstrip en anglais) permet de résoudre ce problème.

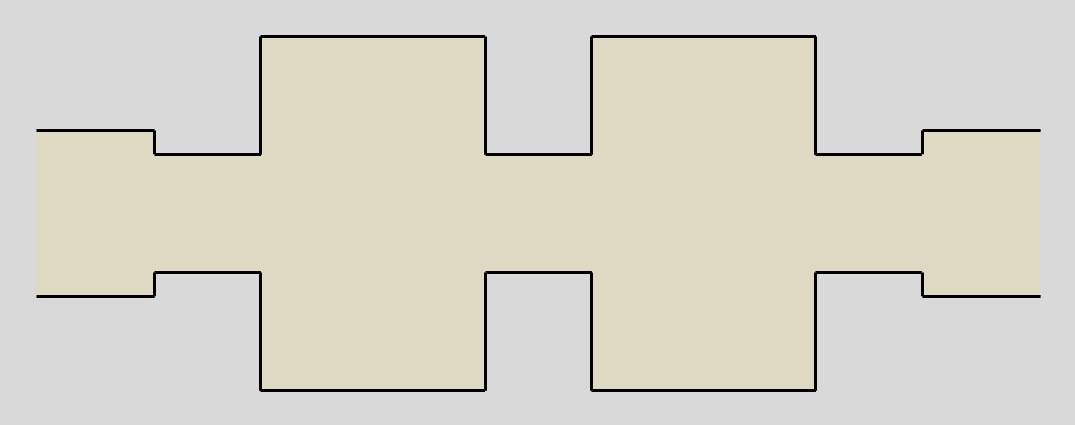Les dimensions d’une pellicule métallique déposée sur un substrat étant calculées à partir des valeurs des éléments \(L,~C\) du filtre, de la longueur \(l\) du tronçon de ligne et de son impédance caractéristique.

On passe du filtre discret ou à constantes localisées au filtre à constantes réparties. Cette dénomination tient à la continuité de la ligne sur son substrat.

Les formules de passage du filtre passe-bas LC polynomial au filtre triplaque sont intégrées dans un processus itératif, car la réalisation des portions de circuit induisent l’apparition d’inductances et de capacités dites secondaires par rapport à celle du passe-bas prototype. Des allers-retours entre le modèle prototype et la réalisation sont nécessaires.

4.1.1. Filtre à quartz

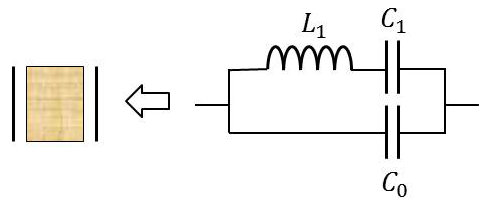Un autre exemple est celui des filtres à quartz. Dans ce cas, les formules sont plus directes, mais il est essentiel de transformer la structure LC de base en dipôles standard pour que l’équivalence puisse se faire.

Désignant par \(L\) la longueur du quartz, \(l\) sa largeur, \(e\) son épaisseur, \(\varepsilon\) sa constante diélectrique, \(\rho\) sa densité,

considérant les caractéristiques d’orientation du cristal : \(d_{12}\) constante piézo-électrique, \(s_{22}\) inverse du module de Young,

on constate que :

\[\begin{aligned} C_0&=\frac{\varepsilon}{4\pi}~\frac{l~L}{e}~\frac{1}{l\times 10^{11}}~F\\ C_1&=\frac{8}{\pi^2}~\frac{d_{22}^2}{s_{22}^2}~\frac{l~L}{e}~\frac{1}{9\times 10^{11}}~F\\ L_1&=\frac{\rho}{8}~\frac{d_{22}^2}{s_{22}^2}~\frac{l~L}{e}~9\times 10^{11}~H\end{aligned}\]

La fréquence de résonance du quartz étant : \[f_R=\frac{1}{21~\sqrt{\rho~s_{22}}}~Hz\]

5. Aperçu sur les filtres passifs à bande étroite

Les filtres passifs à bande étroite sont essentiellement de deux types :

• le filtre sélectif qui privilégie au mieux une petite bande (bande étroite) de fréquences répartie de part et d’autre de cette fréquence (comme une fréquence de résonance) ;

• le filtre réjecteur qui, à l’inverse, élimine le mieux possible une petite bande (bande étroite) de fréquences répartie de part et d’autre de cette fréquence.

5.1. Circuit et fonction de transfert

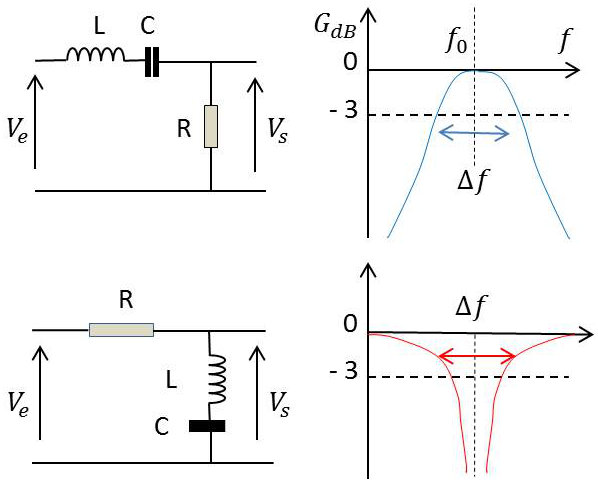On peut imaginer intuitivement que cette opération sera réalisée par un circuit \(LC\) série, supposé sans pertes.

Reportons-nous à la figure ci-contre. Le premier filtre est un filtre sélectif (passe-bande à bande très étroite) comme le montre le graphe de \(G_{dB}(f)\).

Un calcul classique (montage en potentiomètre) permet d’obtenir : \[H(p)=\frac{V_s}{V_e}=\frac{R~C~p}{1+R~Cp+L~C~p^2}\]

On voit que : \[|H(p)|=1\qquad\text{quand :}\quad 1+L~C~p^2=0\]

C’est-à-dire : \[\omega_0=\frac{1}{\sqrt{L~C}}\quad\text{pulsation de résonance}\]

Un même calcul (dual) donnerait pour le circuit réjecteur : \[H(p)=\frac{V_s}{V_e}=\frac{1+L~C~p^2}{1+R~C~p+L~C~p^2}\]

On obtiendrait cette fois \(|H(p)|=0\) d’où une atténuation infinie pour \(\omega=\omega_0\).

5.2. Synthèse

À partir du moment où l’on dispose d’une fonction de transfert explicite, c’est-à-dire exprimée avec les composants eux-mêmes, ce qui a été vu pour la large bande n’a plus lieu d’être ici. La synthèse s’opère par identification directe : coefficients du polynôme physique à coefficients du polynôme mathématique.