1. Position du problème
On peut voir que le transformateur est un quadripôle passif. Il est très connu pour être utilisé dans de multiples applications dans la vie courante, c’est-à-dire en électrotechnique. On le retrouve bien sûr en électronique, mais son étude en électronique est beaucoup plus compliquée, car la fréquence d’alimentation (que l’on connaît pour le 50 Hz) n’est plus constante : elle peut varier cette fois dans un large domaine.
Ce qui nous conduit à faire la distinction entre les transformateurs à noyau de fer, utilisables en BF (de 0 à 20 kHz) et les transformateurs sans fer, utilisables en HF. En effet, aux fréquences élevées, le circuit magnétique doit être supprimé en raisons des pertes fer considérables qui y prendraient naissance (pratiquement proportionnelles au carré de la fréquence).
2. Fuites entre deux circuits couplés
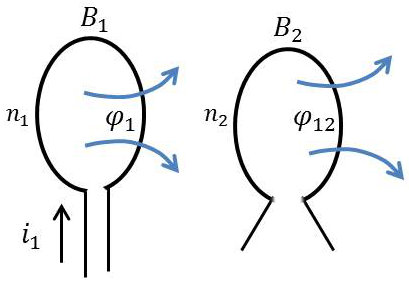 Deux bobines comportent respectivement \(n_1\) et \(n_2\) spires que l’on peut supposer de même surface. Seule la première est alimentée par un courant continu d’intensité \(i_1\).
Deux bobines comportent respectivement \(n_1\) et \(n_2\) spires que l’on peut supposer de même surface. Seule la première est alimentée par un courant continu d’intensité \(i_1\).
Ce courant produit un flux \(\varphi_1\) à travers chacune des spires de cette première bobine. Ce courant produit aussi un flux \(\varphi_{12}\) à travers chacune des spires de la deuxième bobine.
Ce qui nous conduit à introduire respectivement un coefficient d’auto-induction \(L_1\) et un coefficient d’induction mutuelle, on peut écrire : \[L_1~i_1=n_1~\varphi_1\quad;\quad M_1~i_1=n_2~\varphi_{12}\]
La bobine \(B_1\) produit un certain flux à travers la bobine \(B_2\), mais il se produit un flux de fuites par spire que l’on notera : \[\varphi_{f_1}=\varphi_1-\varphi_{12}\]
Désignons par \(l_1\) l’inductance de fuites de la bobine \(B_1\). Le flux total de fuites étant \(n_1\varphi_{f_1}\) on a : \[n_1~\varphi_{f_1}=l_1~i_1=n_1~\varphi_1-n_1~\varphi_{12}\]
On obtient donc : \[l_1=L_1-M~\frac{n_1}{n_2}\qquad\text{[1]}\]
On pourrait opérer en sens inverse, c’est à dire alimenter la bobine \(B_2\) et définir comme précédemment l’inductance de fuites de cette bobine. On aurait alors: \[l_2=L_2-M~\frac{n_2}{n_1}\qquad\text{[2]}\]
L’élimination du rapport \(n_1/n_2\) entre les deux relations conduit à la relation : \[(L_1-l_1)~(L_2-l_2)=M^2\qquad\text{[3]}\]
Faisons à présent l’hypothèse que l’un des enroulements n’a pas de fuites (par exemple \(l_1=0\)) alors que l’autre possède toutes les fuites. On doit alors remplacer l’inductance \(l_1\) par une inductance \(N_1\) appelée inductance de fuites totales de Boucherot. On pourra donc écrire : \[(L_1-l_1)~L_2=M^2\]
D’où les deux relations symétriques :
\[\begin{aligned} &N_1=L_1-\frac{M^2}{L_2}\qquad\text{[4]}\\ &N_2=L_2-\frac{M^2}{L_1}\qquad\text{[5]}\end{aligned}\]
Dans un cas théorique : \[l_1=l_2=0\quad;\quad L_1~L_2=M^2\]
Dans le cas réel : \[L_1~L_2>M^2\]
L’écart entre \(L_1~L_2\) et \(M^2\) caractérise alors l’importance des fuites :
\[\begin{aligned} \sigma&=\frac{L_1~L_2-M^2}{L_1~L_2}\\ N_1&=\sigma~L_1\quad;\quad N_2=\sigma~L_2\end{aligned}\]
On peut ainsi définir un nouveau paramètre, le coefficient de dispersion de Blondel : \[K=\frac{M}{\sqrt{L_1~L_2}}\]
3. Équations du transformateur à noyau de fer
En BF, les transformateurs utilisés en électronique sont des transformateurs industriels, avec noyau de fer.
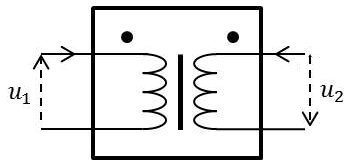 Ils sont représentés symboliquement par deux bobines en mutuelles, séparées par un trait vertical signifiant qu’il s’agit d’un transformateur à noyau de fer. Deux points, placés à proximité des enroulements, indiquent les sens respectifs de ces enroulements.
Ils sont représentés symboliquement par deux bobines en mutuelles, séparées par un trait vertical signifiant qu’il s’agit d’un transformateur à noyau de fer. Deux points, placés à proximité des enroulements, indiquent les sens respectifs de ces enroulements.
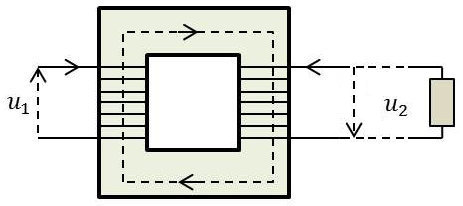 Par convention, si les courants arrivent – ou sortent – tous les deux par les points, les inductions produites par ces courants s’ajoutent ; elles se retranchent dans le cas contraire.
Par convention, si les courants arrivent – ou sortent – tous les deux par les points, les inductions produites par ces courants s’ajoutent ; elles se retranchent dans le cas contraire.
Choisissons un sens positif pour les lignes d’induction dans le circuit magnétique. On en déduit, d’après la règle du tire-bouchon de Maxwell, les sens positifs des courants qui traversent les enroulements primaire et secondaire.
Enfin, pour les sens positifs des tensions, nous adoptons les conventions du système récepteur pour l’enroulement primaire (qui reçoit l’énergie) et les conventions du système générateur pour l’enroulement secondaire (qui alimente la charge).
On peut alors écrire, pour les valeurs instantanées : \[\left\{ \begin{aligned} u_1&=R_1~i_1+n_1~\frac{d\varphi_1}{dt}\\ -u_2&=R_2~i_2+n_2~\frac{d\varphi_2}{dt} \end{aligned} \right.\]
4. Transformateur parfait
Un transformateur parfait est un transformateur idéal dans lequel on néglige :
-
les éléments qui consomment de l’énergie active (résistances primaire et secondaire, hystérésis et courants de Foucault du circuit magnétique) ;
-
les éléments qui consomment de l’énergie réactive (inductances de fuites des enroulements, reluctance du circuit magnétique).
Partant des équations générales : \[\left\{ \begin{aligned} u_1&=n_1\frac{d\varphi}{dt}\\ -u_2&=n_2\frac{d\varphi}{dt}\\ n_1~i_1&+n_2~i_2=0 \end{aligned} \right.\]
et posant : \[m=\frac{n_2}{n_1}\quad;\quad u_2=-m~u_1\quad;\quad i_1=-m~i_2\]
nous pouvons obtenir le circuit équivalent d’un transformateur parfait qui alimenterait une charge d’impédance \(Z_u\).
Ayant adopté le système générateur pour le secondaire, on peut écrire : \[U_2=Z_u~I_2\]
Pour les relations tension – courant secondaires, en fonction des éléments du primaire : \[U_2=-m~U_1\quad;\quad I_2=-\frac{I_1}{m}\quad\Rightarrow\quad U_1=\frac{Z_u}{m^2}~I_1\]
Tout se passe comme si l’impédance \(Z'_u=\cfrac{Z_u}{m^2}\) avait été branchée aux bornes du primaire.
Le transformateur est donc un adaptateur d’impédance.
La téléphonie utilisait beaucoup cette technique dans les premiers centraux électroniques, en particulier dans ce qui s’appelait la transformation dite deux fils quatre fils pour séparer les voies d’émission et de réception pour un abonné téléphonique. Cet organe fondamental de la carte d’abonné portait le nom de transformateur différentiel.
5. Transformateur sans fer
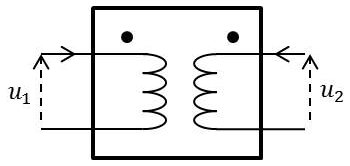 Le problème est plus simple dans le cas des transformateurs sans fer.
Le problème est plus simple dans le cas des transformateurs sans fer.
Dès qu’il y a couplage entre deux inductances, on peut obtenir très simplement un circuit équivalent en traitant le transformateur comme un dipôle passif.
Nous tenons compte des sens positifs habituels pour les courants traversant les deux enroulements, mais adoptons pour les tensions les conventions des quadripôles (système récepteur pour l’entrée et pour la sortie).
Le flux qui traverse les spires du primaire comprend :
-
un flux d’auto-induction toujours positif, les lignes d’induction correspondantes sortant obligatoirement par la face nord des spires ;
-
un flux d’induction mutuelle, positif ou négatif, suivant les cas.
D’après nos notations (gros point et sens positifs des courants), ce dernier a le même signe que le flux d’auto-induction. Ainsi, on a : \[\left\{ \begin{aligned} n_1~\varphi_1=L_1~i_1+M~i_2\\ n_2~\varphi_2=L_2~i_2+M~i_1 \end{aligned} \right.\]
En valeurs instantanées : \[\left\{ \begin{aligned} u_1=R_1~i_1+L_1~\frac{di_1}{dt}+M~\frac{di_2}{dt}\\ u_2=R_2~i_2+L_2~\frac{di_2}{dt}+M~\frac{di_1}{dt} \end{aligned} \right.\]
Si la charge est une résistance pure : \[u_2=-R_2~i_2\]
En valeurs imaginaires : \[\left\{ \begin{aligned} U_1=Z_{11}~I_1+Z_{12}~I_2\\ U_2=Z_{21}~I_1+Z_{22}~I_2 \end{aligned} \right.\]
Si l’on pose : \[\begin{aligned} &Z_{11}=R_1+j~L_1~\omega\\ &Z_{22}=R_2+j~L_2~\omega\\ &Z_{12}=Z_{21}=j~M~\omega \end{aligned}\]
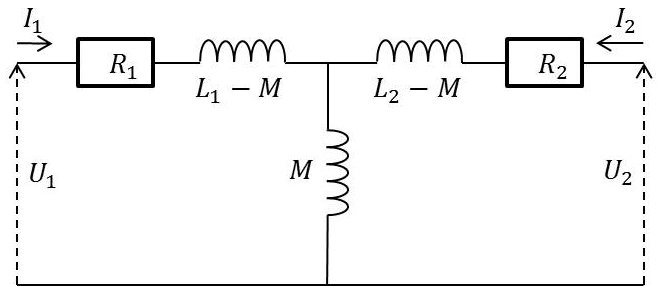 on en déduit le montage en \(T\) équivalent.
on en déduit le montage en \(T\) équivalent.
On sait que (détermination par un essai à vide) : \[m=\frac{n_2}{n_1}=\frac{U_{20}}{U_1}\]
On peut donc écrire : \[\frac{U_{20}}{U_1}=\frac{Z_{21}}{Z_{11}}=\frac{j~M~\omega}{R_1+j~L_1~\omega}\cong\frac{M}{L_1}\]
car la résistance d’un enroulement est généralement négligeable par rapport à sa réactance (\(R_1\ll L_1~\omega\)).
En définitive : \[m~\cong~\frac{M}{L_1}\]

