1. Circuits à constantes réparties

Tout élément d’un conducteur présente une capacité propre et une self propre. Cet effet est particulièrement important :

• dans les fils longs constituant les lignes ;

• dans les fils ou rubans courts en haute fréquence.

Les capacités ou selfs parasites présentant alors des admittances ou impédances notables.

2. Ligne homogène. Équation des télégraphistes

2.1. Établissement de l’équation

Une ligne homogène est constituée par deux circuits filiformes placés côte à côte le long desquels la tension \(V\) et l’intensité \(I\) varient selon la loi : \[\left\{ \begin{aligned} dV=-(r+\Lambda~\frac{\partial}{\partial t})~I~dx\\ dI=-(g+\Gamma~\frac{\partial}{\partial t})~V~dx \end{aligned} \right.\]

• \(r\) : Résistance de la ligne par unité de longueur

• \(\Lambda\) : Inductance de la ligne par unité de longueur

• \(g\) : Conductance de la ligne par unité de longueur (ou perditance)

• \(\Gamma\) : Capacité de la ligne par unité de longueur

Par dérivations successives, on en déduit que \(V\) et \(I\) satisfont à l’équation : \[\frac{\partial^2V}{\partial x^2}=(r+\Lambda~\frac{\partial}{\partial t})~(g+\Gamma~\frac{\partial}{\partial t})~Y\]

C’est l’équation des télégraphistes dont une solution particulière est : \[Y=A~(\omega)~\exp(j~\omega~t\pm\gamma~x)\]

\(\gamma\) étant généralement une fonction complexe de \(\omega\) : \[\gamma=\alpha(\omega)+j~\beta(\omega)\quad;\quad\alpha>0\]

D’où la forme de la solution \[Y_{\pm}=A(\omega)~\exp[\alpha{\omega}\mp j~\beta(\omega)]~\exp(\mp\alpha~x)\]

Et revenant aux équations de définition : \[\frac{V_+}{I_+}=-\frac{V_-}{I_-}=\sqrt{\frac{r+j~\omega~\Lambda}{g+j~\omega~\Gamma}}\]

C’est-à-dire (impédance) : \[\frac{V_+}{I_+}=-\frac{V_-}{I_-}=Z_c^+\]

La solution \(Y_+\) correspond à un signal circulant dans le sens des \(x\) croissant avec une vitesse de phase \(\nu=\omega/\beta\) (fonction de \(\omega\)) et une atténuation (fonction de \(\omega\)). Le signal subit donc une déformation à la fois en phase et en amplitude.

La solution générale est obtenue en combinant les composantes de Fourier \(Y(\omega)\) et en tenant compte des conditions aux limites : \[Y=Y_++Y_-\]

Avec :

\[\begin{aligned} Y_+&=\int_{-\infty}^{+\infty}f_+(\omega)~\exp[j~(\omega~t-\beta~x)]~\exp(-\alpha~x)~d\omega\\ Y_-&=\int_{-\infty}^{+\infty}f_-(\omega)~\exp[j~(\omega~t+\beta~x)]~\exp(+\alpha~x)~d\omega\end{aligned}\]

2.2. Exemple : ligne sans réflexion attaquée à l’entrée

C’est le cas d’une ligne infinie car I et V tendent vers zéro quelle que soit la nature de l’impédance terminale. Seules conviennent les solutions \(Y_+\).

On décompose \(Y_0=Y(x=0)\) en intégrale de Fourier :

\[\begin{aligned} Y_0&=\int_{-\infty}^{+\infty}y(\omega)~\exp(j~\omega~t)~d\omega\\ y(\omega)&=\frac{1}{2~\pi}\int_{-\infty}^{+\infty}Y_0~\exp(-j~\omega~t)~dt\end{aligned}\]

Il vient : \[Y=\int_{-\infty}^{+\infty}y(\omega)~\exp[j~(\omega~t-\alpha)]~\exp(-\alpha~x)~d\omega\]

Pour une ligne sans pertes (\(r=g=0\)) :

\[\begin{aligned} \frac{\partial^2Y}{\partial x^2}&=\Lambda~\Gamma~\frac{\partial^2Y}{\partial t^2}\\ Y&=f\Big(t-\frac{x}{v}\Big)+g\Big(t+\frac{x}{v}\Big)\quad;\quad v=\frac{1}{\sqrt{\Lambda~\Gamma}}\end{aligned}\]

Il y a propagation sans déformation.

Si la ligne est attaquée en \(x = 0\) et que le signal se propage suivant les \(x > 0\) :

• \(f\Big(t-\cfrac{x}{v}\Big)\)  correspond à la somme des signaux émis depuis \(x = 0\) ;

• \(g\Big(t+\cfrac{x}{v}\Big)\)  correspond à la somme des signaux réfléchis à l’extrémité

D’une manière générale, la réflexion s’effectue avec changement de signe :

• pour \(V\) si l’impédance terminale est nulle ;

• pour \(I\) si l’impédance terminale est infinie de manière à annuler \(V\) ou \(I\).

Le signal réfléchi est nul si la ligne est fermée sur l’impédance : \[Z_c=\sqrt{\frac{r+j~\omega~\Lambda}{g+j~\omega~\Gamma}}\]

En effet, la condition \(\cfrac{V_+}{I_+}=Z_c\)  est alors satisfaite en bout de ligne. Cette impédance (dite caractéristique) est indépendante de la fréquence si : \[\frac{r}{g}=\frac{\Lambda}{\Gamma}\]

C’est le cas de la ligne sans perte (\(r\) et \(g\) étant indépendants de \(\omega\)).

3. Ligne homogène : une chaîne de quadripôles

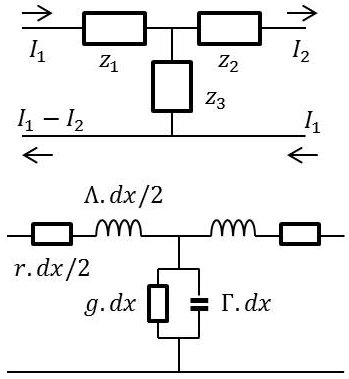Les équations de la ligne sont satisfaites par une cellule en T. La ligne peut être considérée comme une suite de tels quadripôles symétriques :

\[\begin{aligned} &z_1=z_2=\frac{1}{2}~(r+j~\omega~\Lambda)~dx\\ &z_3=\frac{1}{(g+j~\omega~\Gamma)~dx}\end{aligned}\]

3.1. Expression de la matrice impédance

En appliquant la loi des mailles :

\[\begin{aligned} &V_1=z_1~I_1+z_3~(I_1-I_2)\\ &V_2=-z_2~I_2+z_3~(I_1-I_2)\end{aligned}\]

D’où l’expression de la matrice impédance : \[\begin{pmatrix} V_1\\ V_2 \end{pmatrix} = \begin{pmatrix} z_1+z_3& &-z_3\\ z_3& &-(z_2+z_3) \end{pmatrix} \times \begin{pmatrix} I_1\\ I_2 \end{pmatrix}\]

3.2. Expression de la matrice de transfert

On considère cette matrice comme le produit de trois matrices élémentaires, respectivement : \[(\gamma_1)= \begin{pmatrix} 1& &-z_1\\ 0& &1 \end{pmatrix} \quad;\quad (\gamma_2)= \begin{pmatrix} 1& &0\\ -1/z_3& &1 \end{pmatrix} \quad;\quad (\gamma_3)= \begin{pmatrix} 1& &-z_2\\ 0& &1 \end{pmatrix}\]

D’où : \[\begin{pmatrix} V_2\\ I_2 \end{pmatrix} = (\gamma_1)\times(\gamma_2)\times(\gamma_3) \times \begin{pmatrix} V_1\\ I_1 \end{pmatrix}\]

Tous calculs fait : \[\begin{pmatrix} V_2\\ I_2 \end{pmatrix} = \begin{pmatrix} 1+z_1/z_3& &-z_2(1+z_1/z_3)-z_1\\ -1/z_3& &1+z_2/z_3 \end{pmatrix} \times \begin{pmatrix} V_1\\ I_1 \end{pmatrix}\]

Le quadripôle étant symétrique : \[Z_c=\pm\sqrt{\frac{\gamma_{12}}{\gamma_{21}}}=\pm\sqrt{z_1^2+2~z_1~z_3}~\cong~\pm\sqrt{2~z_1~z_3}\]

C’est-à-dire : \[Z_c=\pm\sqrt{\frac{r+j~\omega~\Lambda}{g+j~\omega~\Gamma}}\]

L’étude du cas limite en courant continu (\(\omega=0\)) montre que le signe négatif est à rejeter.

3.3. Quelques remarques

3.3.1. Remarque 1

Une ligne fermée sur \(Z_c\) a une impédance d’entrée égale à \(Z_c\). Il en est encore ainsi si la ligne est infinie, mais l’impédance d’entrée d’une ligne infinie avec pertes est indépendante de l’impédance terminale, car \(V\) et \(I\) y sont nuls. L’impédance d’entrée d’une ligne infinie est donc \(Z_c\).

Réciproquement, une ligne fermée sur \(Z_c\) se comporte comme une ligne infinie, mais \(Z_c\) est en général fonction de \(\omega\), il n’en est en général ainsi que pour un signal monochromatique.

3.3.2. Remarque 2

Dans l’hypothèse où \(r\ll\omega~\Lambda\) et \(g\ll\Gamma\), il vient : \[Z_c~\cong~\sqrt{\frac{\Lambda}{\Gamma}}\quad;\quad\frac{\gamma}{j~\omega}~\cong~-\sqrt{\Lambda~\Gamma}\]

donc réels et indépendants de \(\omega\).

Les signaux sont alors transmis sans déformation à la vitesse \(1/\sqrt{\Lambda~\Gamma}\).

3.3.3. Remarque 3

On peut étudier la propagation par la théorie des quadripôles. La constante de propagation du quadripôle de longueur \(dx\) est : \[\lambda=\frac{I+dI}{I}=\frac{V+dV}{V}=1+\frac{dI}{I}=1+\frac{dV}{V}=1-\gamma\]

\(\lambda\) est valeur propre de la matrice, soit :

\[\begin{aligned} \lambda_+~\lambda_-&=1\\ \lambda_+ +\lambda_-&=\gamma_{11}+\gamma_{22}=2~(1+z_1/z_3)\end{aligned}\]

Ces deux valeurs propres sont donc solution de l’équation du second degré : \[\lambda^2-2~(1+z_1/z_3)~\lambda+1=0\]

Tous calculs faits, on obtient, aux infiniment petits du \(4^o\) ordre en \(dl\) près :

\[\begin{aligned} \lambda_{\pm}&=1-\sqrt{2~z_1/z_3}\\ \lambda_{\mp}&=\frac{1}{1-\sqrt{2~z_1/z_3}}~\cong~1+\sqrt{2~z_1/z_3}+2~z_1/z_3+\dots\end{aligned}\]

Et, aux infiniment petits du second ordre près : \[\gamma=\sqrt{2~z_1/z_3}=\sqrt{(r+j~\omega~\Lambda)(g+j~\omega~\Gamma)}\]

4. Propagation d’un signal BF le long d’une ligne peu selfique

On suppose les composantes de Fourier du signal bornées supérieurement et inférieurement par \(\omega_{sup}\) et \(\omega_{inf}\) telles que : \[\omega_{sup}~\Lambda\ll r\quad;\quad\omega_{inf}\gg g\]

De manière courante en laboratoire : \[1~\rm s^{-1}\ll\omega_{inf}\leq\omega\leq\omega_{sup}\ll 10^6~s^{-1}\]

condition d’ailleurs vérifiée pour les sons audibles.

Il vient : \[Z_c=\sqrt{\frac{r}{j~\omega~\Gamma}}\qquad\text{donc dépendant de}~~\omega.\]

Pour une ligne infinie : \[\gamma=\sqrt{j~\omega~r~\Gamma}=(1+j)~\sqrt{\frac{\omega~r~\Gamma}{2}}\]

5. Propagation d’un signal BF le long d’une ligne peu résistante

On suppose que : \[r\ll\omega\Lambda\quad;\quad g\ll\omega\Gamma\qquad\text{donc :}\quad\omega\gg\frac{r}{\Lambda}\]

Il vient alors : \[Z_c~\cong~\sqrt{\frac{\Lambda}{\Gamma}}\quad;\quad \gamma~\cong~\sqrt{j~\omega~\Gamma~(r+j~\omega~\Lambda)}~\cong~ j~\omega~\sqrt{\Lambda~\Gamma}~\Big(1+\frac{r}{2~j~\omega~\Lambda}\Big)\]

D’où :

\[\begin{aligned} &V=\frac{1}{\sqrt{\Lambda~\Gamma}}\qquad\text{sensiblement indépendant de la pulsation ;}\\ &\alpha~\cong~\frac{r}{2}~\sqrt{\frac{r}{\Lambda}}~\cong~\frac{r}{2~Z_c}\qquad\text{également constant à l’effet de peau près.}\end{aligned}\]

On peut donc raisonner sur une ligne finie fermée sur son impédance caractéristique.

Remarques

1) En \(HF\) (\(\omega\gg r/\Lambda\)), les grandeurs \(Z_c\) et \(V\) sont indépendantes de \(\omega\), mais pour l’atténuation, il faut tenir compte de l’effet de peau.

2) On peut accroître la portée de la ligne en augmentant \(\Lambda\), ce qui diminue en même temps la vitesse de propagation et abaisse la borne inférieure des fréquences où l’approximation est valide, par exemple en intercalant des bobines de self d’une manière régulière (pupinisation).

Simultanément \(Z_c\) est augmentée ce qui peut présenter des inconvénients.

6. Propagation d’une onde HF dans un coaxial

On peut calculer \(\Lambda\) et \(\Gamma\), d’où \(Z_c\) et \(V\).

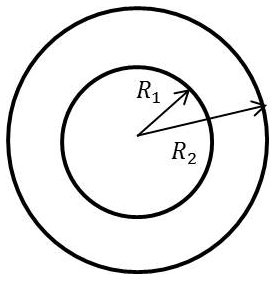Pour la capacité et d’après l’électrostatique : \[\Gamma=\frac{2~\pi~\varepsilon}{\ln(R_2/R_1)}\]

Pour calculer la self, nous ferons appel à l’énergie magnétique emmagasinée dans l’espace entre conducteurs. On supposera que :

• par effet de peau le courant intérieur est superficiel ;

• le champ \(H\) est nul dans le cylindre intérieur.

\[\frac{1}{2}\int_{R_1}^{R_2}\mu~H^2~ds= \frac{1}{2}~\frac{\mu~I^2}{4~\pi^2}\int_{R_1}^{R_2}\frac{2~\pi~r~dr}{r^2}= \frac{1}{2}~\frac{\mu~I^2}{2~\pi^2}~\ln\frac{R_2}{R_1}\]

D’où : \[\Lambda=\frac{\mu}{2~\pi}~\ln\frac{R_2}{R_1}\]

On aurait pu également appliquer la formule du flux, c’est-à-dire : \[\Phi=\Lambda~I=\int\mu~dS\quad;\quad H=\frac{I}{2~\pi~r}\]

La sommation étant faite sur une section méridienne \(dS=I~dr\). On a donc : \[\Phi=\int_{R_1}^{R_2}\frac{\mu~I}{2~\pi}~\frac{dr}{r}=I~\frac{\mu}{2~\pi}~\ln\frac{R_2}{R_1}\]

On écrit ensuite que : \[V=\frac{1}{\sqrt{\Lambda~\Gamma}}=\frac{1}{\sqrt{\mu~\varepsilon}}\]

\(V\) : vitesse de la lumière dans le diélectrique interconducteur.

Par ailleurs : \[Z_c=\sqrt{\frac{\Lambda}{\Gamma}}=\frac{1}{2~\pi}~\sqrt{\frac{\mu}{\varepsilon}}~\ln\frac{R_2}{R_1}\]

On sait que : \[\sqrt{\frac{\mu_0}{\varepsilon_0}}=376~\Omega\]

On construit couramment des lignes de \(Z_c=50~\Omega\).

7. Réflexion à l’extrémité d’une ligne (prise comme origine)

Pour une composante monochromatique, la fonction \(Y\) est une combinaison linéaire de solutions en \(\exp(j~\omega~t\pm\gamma~x)\) avec : \[\gamma=\alpha+j~\beta=\sqrt{(r+j~\omega~\Lambda)~(g+j~\omega~\Gamma)}\]

Ces solutions s’expriment comme :

\[\begin{aligned} v_x&=V_{0+}~\exp(j~\omega~t-\gamma_x)+V_{0-}~\exp(j~\omega~t+\gamma_x)\\ i_x&=I_{0+}~\exp(j~\omega~t-\gamma_x)+I_{0-}~\exp(j~\omega~t+\gamma_x)\end{aligned}\]

Avec : \[\frac{V_{0+}}{I_{0+}}=-\frac{V_{0-}}{I_{0-}}=Z_c\]

Et on voit que : \[\frac{V_{0-}}{V_{0+}}=-\frac{I_{0-}}{I_{0+}}\]

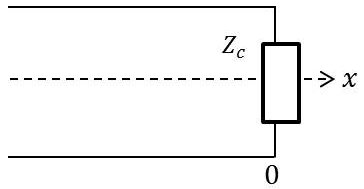Chacun des termes est une onde atténuée en \(\exp(|x|)\) qui se propage à la vitesse de \(\omega/\beta\) :

• dans le sens (+) pour l’onde (+) ;

• dans le sens (–) pour l’onde (–).

Au point \(O~(x=0)\), nous aurons : \[\frac{v_0}{i_0}=Z_0=\frac{V_{0+}+V_{0-}}{I_{0+}+I_{0-}}=Z_c~\frac{I_{0+}-I_{0-}}{I_{0+}+I_{0-}}\]

On postule que le coefficient de réflexion en \(O\) est : \[\rho_0=\frac{V_{0-}}{V_{0+}}=-\frac{I_{0-}}{I_{0+}}\]

On peut alors écrire : \[Z_0=Z_c~\frac{1+\rho_0}{1-\rho_0}\quad;\quad\rho_0=\frac{Z_0-Z_c}{Z_0+Z_c}\]

Notons que :

\(\rho_0=0\) si \(Z_0=Z_c\)     ligne fermée sur son impédance caractéristique ;

\(\rho_0=1\) si \(Z_0=\infty\)     réflexion avec changement de signe pour \(I\) ;

\(\rho_0=-1\) si \(Z_0=0\)    réflexion avec changement de signe pour \(V\).

Remarque 1

Si \(Z_c=0\) (cas particulier de la ligne sans perte) et si \(Z_0=jY_0\) (imaginaire pur), on a : \[\rho_0=\frac{j~Y_0-|Z_c|}{j~Y_0+|Z_c|}\quad;\quad\rho_0^*=\frac{-j~Y_0-|Z_c|}{-j~Y_0+|Z_c|}\]

C’est-à-dire : \[\rho_0~\rho_0^*=1\quad;\quad\|\rho_0|=1\quad;\quad\rho_0=\exp(j~\varphi)\]

Il y a réflexion avec conservation de l’amplitude, mais avec déphasage.

Remarque 2

On peut définir des puissances complexes incidente et réfléchie (dénominations dangereuses en ondes stationnaires) : \[P_+=V_+~I_+^*\quad;\quad P_-=V_+~I_-^*\quad\Rightarrow\quad\frac{P_-}{P_+}=|r^2|\]

En bout de ligne par exemple : \[\frac{P_{0-}}{P_{0+}}=|\rho_0|^2\qquad\text{avec :}\quad\rho_0=\frac{Z_0-Z_c}{Z_0+Z_c}\]

On démontrerait que la puissance complexe absorbée dans \(Z_0\) est : \[P_{0+}-P_{0-}~~~\text{si}~~~r\in\mathbb{R}\qquad\text{et réciproquement.}\]

La puissance moyenne dans le temps absorbée dans \(Z_0\) est : \[\Re[P_{0+}-P_{0-}]~~~\text{si}~~~r\in\mathbb{R}~~~\text{ou si}~~~Z_c\in\mathbb{R} \qquad\text{et réciproquement.}\]

Il ne faut donc utiliser qu’avec circonspection le principe général de conservation de la puissance.

On peut encore démontrer que : \[|\rho_0|=1~~~\text{si}~~~Z_0=\pm j~a~Z_c\qquad a~:~\text{constante réelle quelconque}\]

et réciproquement.

8. Impédance de ligne ramenée à la distance L de l’extrémité

À la distance \(l\) de l’extrémité, l’onde incidente est \(\exp(\gamma~l)\) fois plus intense qu’en bout de ligne. La proportion est inversée pour l’onde réfléchie :

\[\begin{aligned} &i_{-l}=I_{0+}~\exp(j~\omega~t+\gamma~l)+I_{0-}~\exp(j~\omega~t-\gamma~l)\\ &v_{-l}=V_{0+}~\exp(j~\omega~t+\gamma~l)+I_{0-}~\exp(j~\omega~t-\gamma~l)\end{aligned}\]

Soit une impédance apparente :

\[Z_-=\frac{v_-}{i_-}=\frac{V_{0+}+V_{0-}~\exp(-2~\gamma~l)}{I_{0+}+I_{0-}~\exp(-2~\gamma~l)}= Z_c~\frac{I_{0+}-I_{0-}~\exp(-2~\gamma~l)}{I_{0+}+I_{0-}~\exp(-2~\gamma~l)}\]

C’est-à-dire : \[Z_-=Z_c~\frac{1+\rho_0~\exp(-2~\gamma~l)}{1-\rho_0~\exp(-2~\gamma~l)}\qquad;\qquad \rho_0=\frac{V_{0-}}{V_{0+}}=-\frac{I_{0-}}{I_{0+}}\]

On peut encore écrire en ramenant l’origine à la distance \(l\) de l’extrémité :

\[\begin{aligned} &i_{-l}=(I_{l+}+I_{l-})~\exp(j~\omega~t)~\quad;\quad~I_{l\pm}~\exp(\pm\gamma~l)\\ &v_{-l}=(V_{l+}+V_{l-})~\exp(j~\omega~t)\quad;\quad~V_{l\pm}~\exp(\pm\gamma~l) \end{aligned}\]

Avec :

\[\rho_{-l}=\frac{V_{l-}}{V_{l+}}=-\frac{I_{l-}}{I_{l+}}=\frac{V_{0-}}{V_{0+}}~\exp(-2~\gamma ~l)= \rho_0~\exp(-2~\gamma~l)\]

Soit enfin : \[\rho_{-l}=Z_c~\frac{1+\rho_{-l}}{1-\rho_{-l}}\qquad\text{ou}\qquad\rho_{-l}=\frac{Z_{-l}-Z_c}{Z_{-l}+Z_c}\]

Telles sont, jointes aux définitions les relations fondamentales des lignes.

Exemple

Considérons le cas d’une ligne sans perte fermée sur une impédance imaginaire pure (ce cas contient la ligne ouverte \(Z_l=\infty\) ou en court-circuit \(Z_l=0\) ).

On a : \[r=g=0\quad;\quad\gamma=j~\omega~\sqrt{\Lambda~\Gamma}\quad;\quad Z_c=\sqrt{\Lambda~\Gamma}\quad;\quad Z_0=j~Y_0\]

On sait que \(\rho_0\) est alors de module unité : \[\rho_0=\frac{Z_0-Z_c}{Z_0+Z_c}=\exp(-j~2~\varphi)\]

On peut définir la longueur d’onde : \[\lambda=\frac{2~\pi}{\mathcal{I}(\gamma)}=\frac{2~\pi}{\omega~\sqrt{\Lambda~\Gamma}}\]

Il vient alors :

\[\begin{aligned} &\rho_{-l}=\exp\Big\{-j~2~\pi~\Big(\varphi+2~\pi~\frac{l}{\lambda}\Big)\Big\}\\ &Z_{-l}=Z_c~\frac{1+\rho_{-l}}{1+\rho_{-l}}=Z_c~\cot\Big(\varphi+2~\pi~\frac{l}{\lambda}\Big)\end{aligned}\]

Ou encore : \[Z_{-l}=-j~Z_c~\cot\Big(\varphi+2~\pi~\frac{l}{\lambda}\Big)= j~Z_c~\cot\Big(\varphi-\frac{\pi}{2}+2~\pi~\frac{l}{\lambda}\Big)\]

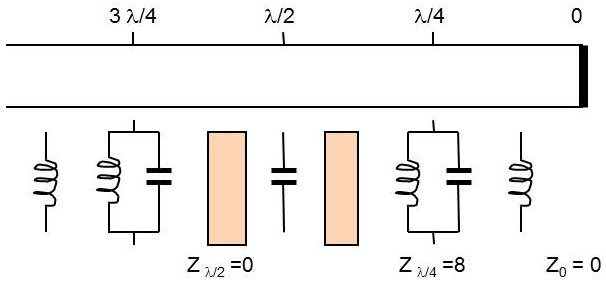C’est une imaginaire pure.

Le schéma ci-contre représente les diverses impédances mesurées à la distance \(l\) variable d’une ligne en court-circuit.

On voit que la périodicité est en \(\lambda/2\). La ligne paraît selfique ou capacitive selon que la tension est en avance sur le courant ou non.

9. Taux d’ondes stationnaires pour une ligne sans pertes

L’onde réfléchie, d’amplitude inférieure ou égale à celle de l’onde incidente, interfère avec elle pour donner en certains points des amplitudes maximales ou minimales.

Le taux d’ondes stationnaires est la grandeur : \[\tau=\frac{|v|_{max}}{|v|_{min}}\]

Les tensions ont leur amplitude maximale aux endroits où l’onde incidente et réfléchie se retrouvent en phase : \[|v|_{max}=|V_{0+}|+|V_{0-}|\]

Au contraire : \[|v|_{min}=|V_{0+}|-|V_{0-}|\]

On a donc : \[\tau=\frac{|V_{0+}|+|V_{0-}| }{|V_{0+}|-|V_{0-}|}=\frac{1+|\rho_0|}{1-|\rho_0|}=\frac{|i|_{max}}{|i|_{min}}\]

On remarquera que : \[\rho_0=1\quad\Rightarrow\quad\tau=\infty\]

Les relations : \[V_+=Z_c~I_+\quad;\quad V_-=-Z_c~I_-\]

montrent que les maximums de courant sont aux minimums de tension.