1. Conductibilité des corps solides

1.1. Solides classiques

Prenant comme référence leur résistivité électrique (ou la conductivité qui est la valeur inverse) les corps solides ont été longtemps classés en trois catégories, respectivement :

1. les métaux, de \(1,6\times 10^{-8}~\rm\Omega~m\) (argent Ag) à \(9,5\times 10^{-7}~\rm\Omega~m\) (mercure Hg), croissante avec un échauffement ;

2. les mauvais conducteurs, approximativement de \(10^{-1}~\rm\Omega~m\) à \(10^4~\rm\Omega~m\), décroissante avec un échauffement ;

3. les bons isolants, au moins égale à \(10^{10}~\rm\Omega~m\), décroissante avec un échauffement.

Cependant, on a remarqué que certains métaux pouvaient acquérir une résistivité supérieure à celle de certains mauvais conducteurs et que les isolants devenaient moins résistants lorsqu’ils étaient portés à une certaine température. Un tel classement était donc remis en cause.

1.2. Semi-conducteurs

Les mauvais conducteurs sont ainsi devenus les semi-conducteurs que nous connaissons. Et leurs propriétés ne pouvaient être étudiées que dans les contextes théoriques de la physique quantique et de la mécanique ondulatoire.

C’était la naissance de notre électronique miniaturisée. Conséquence de cette miniaturisation : le couplage étude théorique quantique – étude expérimentale devait être finement considéré.

Pour preuve, la sensibilité de réaction des propriétés électriques à des traces d’impuretés. Pour fixer les idées : l’introduction d’un atome d’antimoine (Sb) pour 100 millions d’atomes de germanium (\(Ge\)) suffit à faire passer la résistivité de \( \rho=47\text{ à }0,038~\rm\Omega~m\).

De plus, dès 1833, Faraday avait remarqué que la résistivité du sulfure d’argent (\(Ag_2S\)) diminue quand la température s’élève. Ce phénomène, inverse de celui présenté par les métaux, a été observé sur de nombreux autres semi-conducteurs.

Un autre phénomène pour certains semi-conducteurs : l’existence d’un intervalle de température à l’intérieur duquel la résistivité est stationnaire, voire croissante avec la température.

2. Porteurs de charge : conductions n et p

Le phénomène de Hall a permis d’établir le signe et la concentration des porteurs de charge.

Dans le cas des métaux, le nombre de porteurs de charges (électrons) par unité de volume ne dépend pas de la température. C’est la diminution de leur mobilité par échauffement qui est la cause de l’augmentation observée de la résistivité avec la température.

Dans le cas des semi-conducteurs, l’augmentation rapide du nombre des porteurs de charge par unité de volume avec la température est la cause fondamentale de la diminution de résistivité. Les mobilités varient peu (légère décroissance avec la température).

Le phénomène de Hall a montré qu’il existe :

• des semi-conducteurs où les porteurs de charge sont en majorité négatifs (semi-conducteurs dits de type n), les porteurs de charge majoritaires étant les électrons ;

• d’autres semi-conducteurs où les porteurs majoritaires de charge sont positifs (semi-conducteurs dits de type p), les porteurs de charge majoritaires étant appelés des trous.

Un trou n’existe que parce qu’il manque alors un électron. Notion étrange qui n’aura d’explication physique sérieuse qu’avec l’étude de la théorie des bandes d’énergies des électrons dans les cristaux.

Les électrons et les trous constituent des paires : ils sont donc en nombre identique, mais un trou n’existe que parce qu’un électron de la bande de valence a quitté sa place pour occuper un état de la bande de conduction. C’est ce qui fait la caractéristique du semi-conducteur de type intrinsèque.

Dans tous les semi-conducteurs, la conductibilité est produite à la fois par le déplacement d’électrons et par celui des trous.

Analogie

La conduction par les électrons est immédiate. Celle par les trous, à priori virtuelle, est moins immédiate. Une situation classique peut permettre d’éclaircir la perception du phénomène.

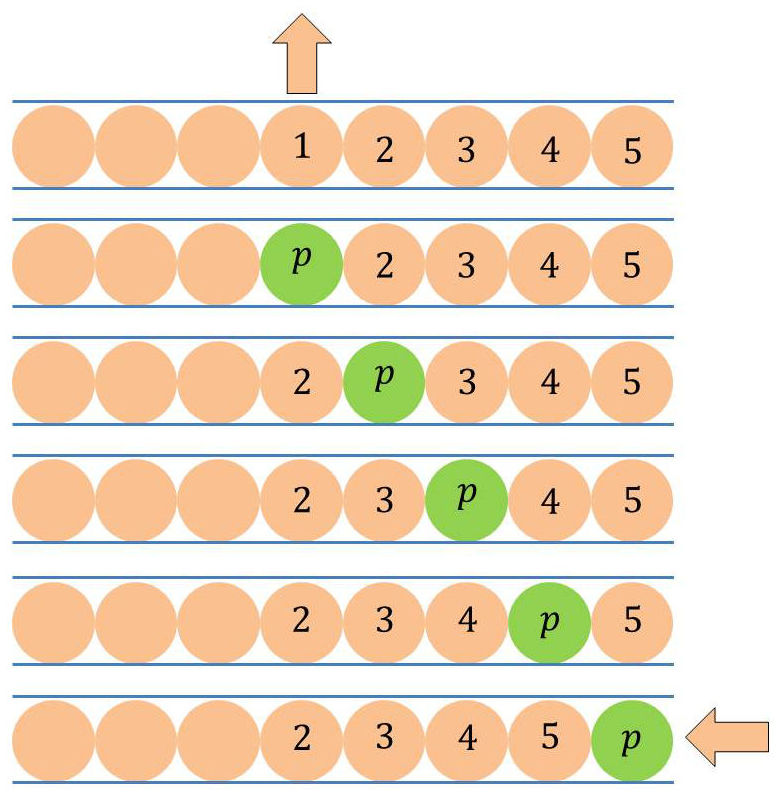Prenons l’image d’une rangée de billes logées dans des alvéoles, dans un tube qui ne peut être alimenté que par la droite. Imaginons qu’une bille 1 (n) puisse quitter le tube à sa hauteur moyennant une ouverture momentanée pour retrouver un autre tube.

Elle laisse une alvéole vide qui sera occupée par la bille voisine (2) qui laisse son alvéole vacante à la bille voisine (3) et ainsi de suite. Ceci jusqu’à ce que la dernière alvéole soit vacante pour une future bille (n).

Tout se passe comme si l’alvéole (p) s’était déplacée vers la droite. Si ces boules étaient chargées — électrons —, ce mouvement constituerait de la conduction électrique. C’est à ce processus que s’apparente la conduction d’électricité, mais à l’aide de trous.

3. Spécificités électriques

En plus de l’augmentation rapide du nombre des porteurs de charge avec la température, cause de la diminution de résistivité généralement observée, les semi-conducteurs présentent de très intéressantes propriétés dont les principales sont :

• grande facilité de production d’effets électriques non linéaires : redressement, variation de capacité avec la tension appliquée ;

• constante de Hall élevée ;

• effets photoélectriques variés ;

• effet thermoélectrique élevé.

C’est l’existence de propriétés électriques non linéaires dans des dispositifs simples (diodes) qui a permis le grand développement des redresseurs à semi-conducteurs. C’est l’emploi de dispositifs plus élaborés (transistors, diodes tunnel etc.) qui a donné un véritable essor à l’électronique des semi-conducteurs. Ce sont les propriétés électriques des semi-conducteurs qui sont aujourd’hui les plus importantes par leurs applications.

L’étude du mécanisme de la conductibilité du milieu semi-conducteur est fondamentale.