1. Bruit de deux résistances en parallèle
1.1. Énoncé
Une résistance métallique \(R_1\) de \(5\times 10^5~\Omega\), plongée dans l’azote liquide à 77 K, est placée en parallèle avec une résistance \(R_2\) de \(10^5~\Omega\) à 20 °C.
Quelles sont la tension et la puissance de bruit résultantes pour une bande passante de 15 kHz ?
1.2. Solution
Rappelons l’expression classique de la tension quadratique de bruit aux bornes d’une résistance à la température absolue \(T\) : \[\overline{e^2}=4~k~T~R~\Delta F\qquad\text{avec :}\quad k=1,38\times 10^{-23}~J~K^{-1}\qquad \text{constante de Boltzmann}\]
Notons que \(T_2=(20+273)~K\).
Les résistances étant en dérivation, les intensités quadratiques (ou puissances) s’ajoutent : \[\overline{i^2}=\overline{i_1^2}+\overline{i_2^2}=4~k~\Delta F~\Big(\frac{T_1}{R_1}+\frac{T_2}{R_2}\Big)\qquad(\text{numériquement}~2,25\times 10^{-21}~A^2)\]
Introduisant la résistance équivalente classique : \[R=\frac{R_1~R_2}{R_1+R_2}\qquad(\text{numériquement}~83~000~\Omega)\]
Pour la tension quadratique de bruit : \[\overline{e^2}=2,52\times 10^{-21}~(83~000)^2=17,3\times 10^{-12}~V^2\]
D’où la tension de bruit : \[e_b=\sqrt{\overline{e^2}}=4,15~\mu V\]
2. Comparaison des bruits de résistance et de diode
2.1. Énoncé
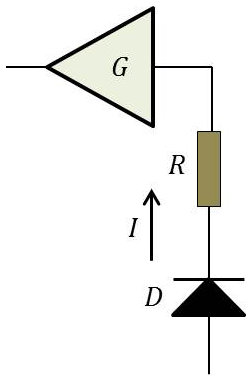Une diode saturée laisse passer un courant de 0,1 mA. Elle est placée en série avec une résistance \(R\) de \(5\times 10^4~\Omega\) montée aux bornes d’un amplificateur de gain \(10^4\) et de largeur de bande efficace de 20 kHz.
Quelles sont les tensions de sortie dans les cas respectifs suivants ?
-
diode dite éteinte (non active, équivalente à un court-circuit pour sa résistance extrêmement petite) ;
-
diode dite allumée (active), sachant que l’amplificateur ne génère pas de bruit.
2.2. Solution
1. Quand la diode est éteinte, la résistance étant seule active, il lui correspond la tension quadratique de bruit (en entrée de l’amplificateur) : \[\overline{e^2}=4~k~T~R~\Delta F\qquad(\text{numériquement}~16\times 10^{-12}~V^2)\]
À la sortie : \[\overline{v_s^2}=G^2~\overline{e^2}\qquad (\text{numériquement}~(10^4)^2~16\times 10^{-12}=16\times 10^{-4}~V^2)\]
D’où la tension de bruit en sortie : \[\sqrt{\overline{v_s^2}}=0,04~V\]
1. Quand la diode est allumée, le courant de fluctuation dû à la diode a pour expression : \[\overline{i^2}=2~e~I_p\Delta F\qquad\text{avec :}\quad e=1,6\times 10^{-19}~C\qquad\text{charge élémentaire}\]
D’où la tension aux bornes de \(R\) : \[\overline{e_2^2}=R^2~\overline{i^2}\qquad(\text{numériquement}~16\times 10^{-10}~V^2)\]
En tenant compte cette fois des deux composants, nous avons en entrée de l’amplificateur (somme quadratique): \[\overline{v_e^2}=\overline{v_1^2}+\overline{v_2^2}\qquad(\text{numériquement}~1~616\times 10^{-12}~V^2)\]
Tension quadratique de sortie : \[\overline{v_s^2}=G^2~\overline{v_e^2}\]
D’où la tension de bruit de sortie : \[\sqrt{\overline{v_s^2}}=0,4~V\]
