1. Exercice 1
1.1. Énoncé
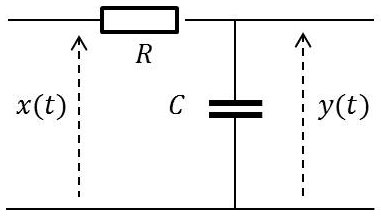On considère le filtre RC représenté ci-contre. Le signal entrant \(x(t)\) est supposé déterministe.
-
Donner l’expression de sa fonction de transfert \(H(f)\) en partant des équations différentielles qui régissent le fonctionnement du filtre.
-
Donner l’expression de la réponse impulsionnelle de ce filtre.
-
Quelle est la nature du filtre ? Est-il causal ? Est-il stable ?
1.2. Solution
1) Application de la loi d’Ohm classique : \[x(t)=R~i(t)+y(t)\]
Calcul classique de l’intensité : \[y(t)=\frac{1}{C}\int i(t)~dt\quad\Rightarrow\quad i(t)=C~\frac{dy(t)}{dt}\]
D’où l’équation différentielle aux tensions : \[x(t)=R~C~\frac{dy(t)}{dt}+y(t)\]
Transformation de Fourier : \[X(f)=j~2\pi~f~R~C~Y(f)+Y(f)\]
Expression de la fonction de transfert : \[H(f)=\frac{Y(f)}{X(f)}=\frac{1}{1+j~2\pi~f~R~C}=\frac{1}{1+j~\cfrac{f}{f_c}}\quad;\quad f_c=\frac{1}{2\pi~R~C}\]
2) On sait que :
\[\begin{aligned} &h(t)=F^{-1}[H(f)] \\ &F^{-1}\Big[\frac{1}{\alpha+j2\pi~f}\Big]=u(t)~\exp(-\alpha~t)\quad;\quad u(t)~~\text{fonction de Heaviside} \end{aligned}\]
On a ici : \[H(f)=\frac{1/R~C}{1/R~C+j~2\pi~f}\quad\Rightarrow\quad h(t)=\frac{1}{R~C}~u(t)~\exp(-\frac{t}{R~C})\]
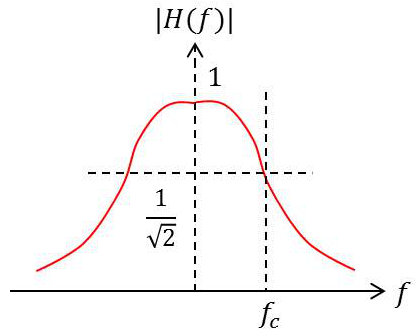3) Intuitivement, on voit dans l’expression de \(|H(f)|\) qu’il s’agit d’un filtre passe-bas, car \(|H|\rightarrow 0\) quand \(f\rightarrow\pm\infty\).
C’est d’ailleurs ce que montre le tracé de : \[|H(f)|=\frac{1}{\sqrt{1+4\pi^2~f^2~R^2~C^2}}\]
L’expression de la réponse impulsionnelle montre qu’il y a causalité \(h\rightarrow 0\) quand \(t\rightarrow\infty\).
La stabilité est tout aussi intuitive : \[\int_{-\infty}^{+\infty}|H(t)|~dt=\frac{1}{R~C}\int_0^{+\infty}\exp(-t/R~C)~dt=1 ~~ <+\infty\]
2. Exercice 2
2.1. Énoncé
Un signal x(t) dont le spectre est limité à la bande \([-B,~+B]\) traverse un filtre dont la fonction de transfert est donnée par: \[H(f)=|H(f)|~\exp[j~\Phi(f)]\]
Avec :
\[\begin{aligned} &|H(f)|=A+\alpha~\cos\frac{\pi~f}{B}\quad;\quad A>\alpha>0\\ &\Phi(f)=-2\pi~f~t_0\quad;\quad t_0>\frac{1}{2~B}\qquad\qquad\qquad\text{si}~~|f|\leq B\\ &H(f)=0\qquad\qquad\qquad\qquad\qquad\qquad\qquad~~\text{si}~~|f|>B\end{aligned}\]
-
Donner l’expression du signal \(y(t)\) à la sortie du filtre en fonction du signal d’entrée \(x(t)\).
-
Interprétation physique.
2.2. Solution
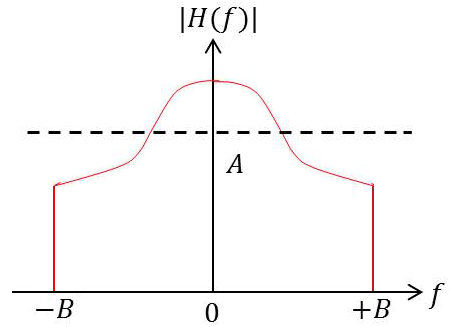Remarques préliminaires
La représentation graphique de \(|H(f)|\) montre qu’il s’agit d’un filtre réel, donc non idéal (forme créneau), ce qui va se traduire par des apparitions de distorsions.
1) Calcul de \(y(t)\)
On part de la transformée de Fourier : \[Y(f)=H(f)~X(f)=(A+\alpha~\cos\frac{\pi~f}{B})~\exp(-j~2\pi~f~t_0)~X(f)\]
En décomposant compte tenu de l’expression complexe du cosinus :
\[\begin{aligned} Y(f)=\big\{A~\exp(-j~2\pi~f~t_0) &+\frac{\alpha}{2}~\exp(j~\pi~f/B)\exp(-j~2\pi~f~t_0) \\ &+\frac{\alpha}{2}~\exp(-j~\pi~f/B)\exp(-j~2\pi~f~t_0)\big\}~X(f)\end{aligned}\]
Ou encore :
\[\begin{aligned} Y(f)=A~\exp(-j~2\pi~f~t_0)~X(f) &+\frac{\alpha}{2}~\exp\{-j~2\pi~f~(t_0-1/2B)\}~X(f) \\ &+\frac{\alpha}{2}~\exp\{-j~2\pi~f~(t_0+1/2B)\}~X(f)\end{aligned}\]
Sachant par ailleurs que : \[F^{-1}[\exp(-j~2\pi~f_a)~X(f)]=x(t-a)\]
On obtient donc : \[y(t)=A~x(t-t_0)+\frac{\alpha}{2}~x(t-t_0+1/2B)+\frac{\alpha}{2}~x(t-t_0-1/2B)\]
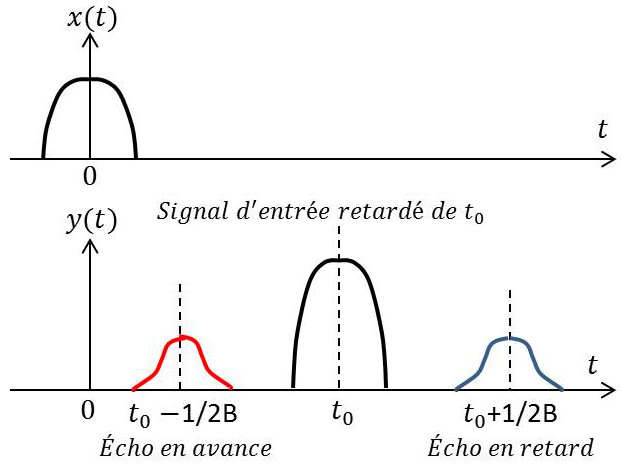2) Interprétation physique
Le premier terme \(A~x(t-t_0)\) représente la partie principale du signal d’entrée retardée de \(t_0\) (ce que l’on aurait obtenu avec un filtre idéal).
Le deuxième terme représente un écho, en avance de \(1/2B\).
Le troisième terme représente un écho, en retard de \(1/2B\).
On entend par distorsion du signal d’entrée introduite par le filtre, la présence de ces deux échos.
