1. Groupe

1.1. Définitions

Un groupe est un ensemble muni d’une loi de composition interne satisfaisant aux trois conditions suivantes :

• la loi est associative ;

• il existe un élément neutre ;

• tout élément a un inverse.

Si de plus la loi est commutative, le groupe est dit abélien.

Un groupe peut être fini (d’ordre \(N\) s’il y a \(N\) termes) ou infini dans le cas contraire.

Exemples

1. Ensemble des entiers avec (zéro inclus) muni de la loi d’addition.

2. Ensemble des réels positifs (zéro exclu) muni de la loi de multiplication.

3. L’ensemble \(E\) : {1, -1, i, -i}, muni de la loi de multiplication, est un groupe d’ordre 4.

4. Les transformations de la géométrie peuvent être rassemblées en divers groupes où la loi de transformation est invariablement celles de la composition des transformations.

   Pour nous borner à la géométrie plane : le groupe des translations, le groupe des rotations, le groupe des déplacements, le groupe des similitudes directes, le groupe des symétries, etc.

   La loi de composition reprend la notion de l’application composée : \[z(x)=g[f(x)]\qquad\text{traduit par :}\quad z=g\circ f\]

   Dans chacun de ces groupes, comme dans tout groupe de transformation, l’élément neutre est la transformation identique.

1.2. Table de multiplication d’un groupe

Nous raisonnerons sur un exemple concret. Considèrons l’ensemble des six transformations \(T\) à une variable qui interviennent dans l’étude des divers rapports anharmoniques d’un système à quatre nombres et dont la première (\(T_0\)) est l’opération identique :

\[\begin{aligned} &T_0(x)=x &&T_1(x)=\frac{1}{x} &&T_2(x)=1-x\\ &T_3(x)=\frac{1}{1-x} &&T_4(x)=\frac{x-1}{x} &&T_5(x)=\frac{x}{1-x}\end{aligned}\]

Ces six opérations forment un groupe vis-à-vis de la loi de composition, notée ici \(\textsf{L}\) : \[T_i(x)~\textsf{L}~T_j(x)=T_j[T_i(x)]\]

C’est-à-dire : \[T_j\circ T_i\]

\(i\) et \(j\) désignant, indépendamment l’un de l’autre, deux indices prélevés sur la suite {0, 1, 2, 3, 4, 5} et qui n’est autre que la loi définissant l’opération des opérations : \[x'=T_i(x)\quad;\quad x''=T_j(x')\]

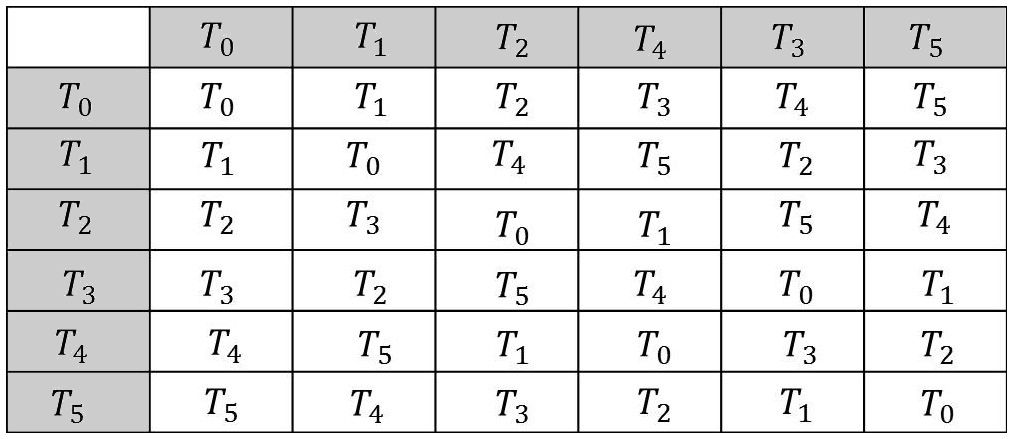Les résultats des calculs sont disposés dans une table de multiplication du groupe, présentée à la manière d’une table de Pythagore.

Chaque case intérieure porte l’opération [\(T_i~\textsf{L}~T_j\)], résultante de celle de \(T_i\) portée en tête de ligne et de celle de \(T_j\) portée en tête de colonne.

L’examen de cette table montre que \(\textsf{L}\) est bien une loi interne sur l’ensemble \(\{T\}\) :

• On peut vérifier que \(T_0\) est l’élément neutre de cette loi.

• On peut vérifier qu’à chacune des opérations (\(T_1,~T_2,~T_3,~T_4,~T_5\)) correspond son inverse, à savoir (\(T_1,~T_2,~T_4,~T_3,~T_5\)) respectivement.

Les axiomes de la structure de groupe sont bien vérifiés.

Examinons, d’après la table de multiplication du groupe, quelles sont les puissances successives des opérations :

\[\begin{aligned} &T_0~: &&(T_0)^2=T_0 &&\dots\\ &T_1~: &&(T_1)^2=T_0 &&(T_1)^3=T_1 &&\dots\\ &T_2~: &&(T_2)^2=T_0 &&(T_2)^3=T_2 &&\dots\\ &T_3~: &&(T_3)^2=T_4 &&(T_3)^3=T_0 &&(T_3)^4=T_3 &&\dots\\ &T_4~: &&(T_4)^2=T_3 &&(T_4)^3=T_0 &&(T_4)^4=T_4 &&\dots\\ &T_5~: &&(T_5)^2=T_0 &&(T_5)^3=T_5 &&\dots\end{aligned}\]

On voit que {\(T_1,~T_2,~T_5\)} sont des opérations identiques à leurs inverses ou opérations involutives.

D’autres part, {\(T_3,~T_4\)} reproduisent l’opération unité après trois itérations, c’est-à-dire que leurs puissances à l’une et à l’autre possèdent la propriété de fermeture triangulaire.

Chacun des ensembles formés par {\(T_0,~T_1\)}, par {\(T_0,~T_2\)}, par{\(T_0,~T_3\)}, par {\(T_0,~T_3,~T_4\)} est un sous-groupe de {\(T\)}. Ces sous-groupes, respectivement formés des puissances successives de \(T_1\), de \(T_2\), de \(T_5\) et par exemple de \(T_3\) sont des groupes cycliques.

1.3. Groupes particuliers

1.3.1. Substitutions

Considérant N objets {\(a,~b,~c,~\dots,~l\)}, on appelle substitution la transformation par laquelle on passe d’une permutation de ces objets à une autre. Une telle opération est définie par les rangs nouveaux (\(r_1,~r_2,~\dots,~r_n\)) que viennent prendre dans la deuxième permutation les objets occupant dans la première les rangs (\(1,~2,~\dots,~n\)).

Exemple : Groupe {\(a,~b,~c\)} à trois lettres

Élément neutre : \[E: \begin{pmatrix} a&b&c\\ a&b&c \end{pmatrix}\]

Il y a naturellement (\(3~!=6\)) possibles (groupe fini d’ordre 6) : \[A: \begin{pmatrix} a&b&c\\ b&c&a \end{pmatrix} \quad B: \begin{pmatrix} a&b&c\\ c&a&b \end{pmatrix} \quad C: \begin{pmatrix} a&b&c\\ b&a&c \end{pmatrix} \quad D: \begin{pmatrix} a&b&c\\ a&c&b \end{pmatrix} \quad F: \begin{pmatrix} a&b&c\\ c&b&a \end{pmatrix}\]

Pour la construction de \(A\), on a pris : \(r_1=2~,~r_2=3~,~r_3=1\).

Si on adopte la loi de multiplication (opération en séquence) : \[C\cdot B= \begin{pmatrix} a&b&c\\ c&b&a \end{pmatrix} =D \quad;\quad B\cdot C= \begin{pmatrix} a&b&c\\ a&c&b \end{pmatrix} =F\]

On constate que ce groupe est non abélien (non commutation).

Table de multiplication

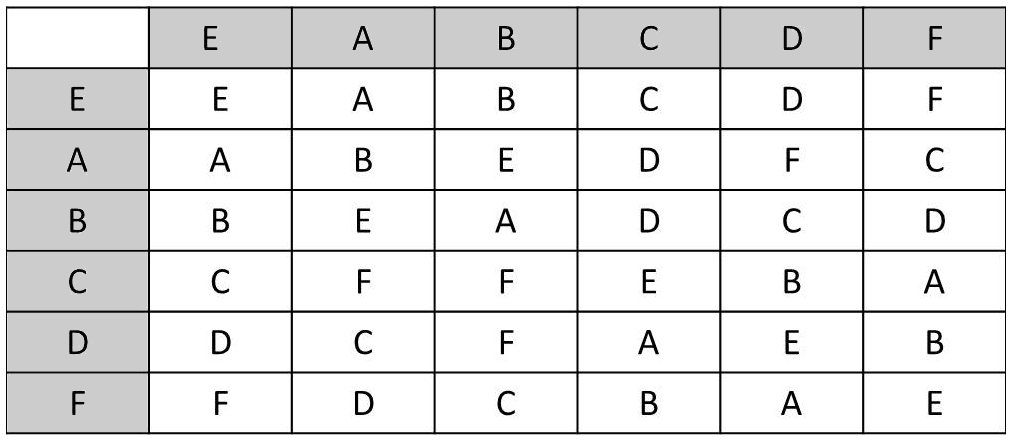La table de multiplication est élaborée en répétant l’opération précédente avec toutes les combinaisons de couples possibles, en tenant compte de l’existence de l’élément neutre \(E\).

On peut donc exploiter cette opération neutre pour rechercher l’inverse d’une opération. Recherchons par exemple \(I\) inverse de \(C\), en écrivant que \(I\cdot C=E\) : \[\begin{pmatrix} a&b&c\\ b&a&c \end{pmatrix} \begin{pmatrix} a&b&c\\ x&y&z \end{pmatrix} = \begin{pmatrix} a&b&c\\ a&b&c \end{pmatrix}\]

Ou encore : \[\begin{pmatrix} a&b&c\\ y&x&z \end{pmatrix} = \begin{pmatrix} a&b&c\\ a&b&c \end{pmatrix}\]

On a donc : \[y=a\quad;\quad x=b\quad;\quad z=c\]

On peut écrire : \[I= \begin{pmatrix} a&b&c\\ b&a&c \end{pmatrix} =C\]

On peut en conclure que : \(C\cdot C=E\)

1.3.2. Transpositions

On dit qu’il y a transposition lorsque, dans une substitution, il y a échange de deux objets, tous les autres conservant leurs places respectives.

Un exemple de transposition (de \(\beta\) et \(\gamma\)) : \[\begin{pmatrix} a&\beta&c&d&\gamma\\ a&\gamma&c&d&\beta \end{pmatrix}\]

Théorème

Toute substitution de degré N est réductible à un produit de transpositions.

Remarque

La réduction d’une substitution de degré N à un produit de transpositions est possible de plusieurs manières. Considérons par exemple la substitution : \[\begin{pmatrix} a&b&c&d\\ b&d&a&c \end{pmatrix}\]

Elle peut être décomposée en les 3 transpositions réalisant la suite des permutations : \[(a,~b,~c,~d)\quad;\quad(b,~a,~c,~d)\quad;\quad(b,~a,~d,~c)\quad;\quad(b,~d,~a,~c)\]

ou bien encore en les 5 transpositions réalisant la suite : \[(a,~b,~c,~d)\quad;\quad(a,~b,~d,~c)\quad;\quad(d,~a,~b,~c)\quad;\quad(d,~b,~a,~c)\quad;\quad(b,~d,~a,~c)\]

sachant que d’autres manières sont encore possibles.

1.3.3. Substitutions circulaires

Nous raisonnons sur un exemple à 5 objets (\(a,~b,~c,~d,~e\)) dont les représentations sont (\(A,~B,~C,~D,~E\)) et dans cet ordre déterminé, le sens positif étant celui du cercle trigonométrique.

On appelle substitution circulaire selon le schéma : \[a~~\rightarrow~~b~~\rightarrow~~c~~\rightarrow~~d~~\rightarrow~~e~~\rightarrow~~a\]

la substitution qui consiste, étant donné une permutation initiale quelconque de 5 objets, à remplacer chacun de ces objets par celui qui suit (cf. figure).

Cette substitution peut se représenter par la notation : \[\begin{pmatrix} a&b&c&d&e\\ b&c&d&e&a \end{pmatrix}\]

soit : \[r_1=2\quad;\quad r_2=3\quad;\quad r_3=4\quad;\quad r_4=5\quad;\quad r_5=1\]

Théorème

Toute substitution peut se décomposer en un produit de substitutions circulaires disjointes, et cela d’une seule manière à l’ordre des facteurs près.

1.4. Morphisme de groupes : isomorphisme et endomorphisme

Un exemple de morphisme que nous appliquions sans le savoir, à l’époque de notre baccalauréat, celui du calcul logarithmique. La multiplication dans un espace devenant une addition dans l’autre espace, avec des nombres moins impressionnants. Avec cette possibilité de travailler entièrement dans un espace pour revenir au premier espace à la fin des opérations.

De manière plus sérieuse :

Soient deux groupes \(F\) et \(G\) muni chacun d’une loi de composition interne, respectivement : \[(F~,~\top)\quad\text{et}\quad(G~,~\bot)\]

On dit qu’une application f de F dans G est un morphisme de groupes si, pour tout couple (\(x,~y\)) de \(F\) : \[F(x~\top~y)=f(x)~\bot~f(y)\]

Si \(f\) est un morphisme bijectif, on dit qu’il y a isomorphisme. Les groupes \(F\) et \(G\) sont dits alors isomorphes et on note (\(F~\cong~G\)).

Le morphisme d’un groupe \(G\) dans lui-même est un endomorphisme.

Exemples d’isomorphisme :

– La fonction logarithme népérien est un isomorphisme du groupe multiplicatif (\(\mathbb{R}^{+*},~\times\)) sur le groupe additif (\(\mathbb{R},~+\)).

– La fonction exponentielle (base \(e\)) est un isomorphisme du groupe additif (\(\mathbb{R},~+\)) sur le groupe multiplicatif (\(\mathbb{R}^{+*},~\times\)).

Considérons la fonction exponentielle complexe : \[\mathbb{C}~~\rightarrow~~\mathbb{C}^*\qquad\qquad z~~\mapsto~~e^z\]

Elle vérifie : \[e^{z+z'}~=~e^z\times e^{z'}\]

Il s’agit bien d’un morphisme de groupes de (\(\mathbb{C},~+\)) dans (\(\mathbb{C}^*,~\times\)). Et par restriction de (\(\mathbb{R},~+\)) dans (\(\mathbb{R}^{+*},~\times\)).

2. Classes

2.1. Transformé, conjugué

Soient \(\{A,~B,~X\}\in~G\). \(A\) est dit transformé de \(B\) par \(X\) si : \[X^{-1}~B~X=A\]

De plus : \[\forall~A~\text{et}~B~:\quad\text{si}~\exists~X~~\text{tel que :}\quad A=X^{-1}~B~X\]

Alors, \(A\)  \(B\) sont dits conjugués (la conjugaison étant l’opération liant \(A\) et \(B\)).

C’est une relation d’équivalence réflexive, symétrique et transitive (RST).

– Réflexive (\(A\) conjugué de \(A\)) : \[A=X^{-1}~A~X\]

– Symétrique (\(A\) conjugué de \(B\quad\Rightarrow\quad B\) conjugué de \(A\)) :

\[\begin{aligned} &A=X^{-1}~B~X \\ &X~A=B~X\qquad\qquad~~~\text{après multiplication à gauche par}~X\\ &X~A~X^{-1}=B\qquad\qquad\text{après multiplication à droite par}~X^{-1}\\ \text{ou encore :}\quad~\\ &B=(X^{-1})^{-1}~A~(X^{-1})\end{aligned}\]

On voit que \(B\) est transformé de \(A\) par \(X^{-1}\). De ce fait, \(B\) est conjugué de \(A\).

– Transitive (\(A\) conjugué de \(B\) et \(B\) conjugué de \(C\quad\Rightarrow\quad A\) conjugué de \(C\)) :

\[\begin{aligned} &A~\text{conj.}~C\qquad~A=X^{-1}~C~X\\ &B~\text{conj.}~C\qquad~B=Y^{-1}~C~Y\quad\Rightarrow\quad C=Y~B~Y^{-1}\\ &A=X^{-1}~(Y~B~Y^{-1})~X=(Y^{-1}~X)~B~(Y^{-1}~X)\end{aligned}\]

\(A\) est transformé de \(B\) par \((Y^{-1}~X)\).

2.2. Classes d’équivalence ou classes

On appelle classe d’un élément \(A\in G\) l’ensemble des éléments {\(X^{-1}~A~X\)} quand \(X\) parcourt le groupe \(G\), c’est-à-dire quand il prend toutes les valeurs.

2.3. Élément neutre E

\[X^{-1}~E~X=E\qquad\text{quand}~X~\in~G\]

\(E\) forme donc une classe à lui seul.

2.4. Groupe abélien

\[A\quad\text{tel que :}\quad X^{-1}~A~X=A~X~X^{-1}~A=A\]

Dans un groupe abélien, tout élément forme une classe à lui seul.

2.5. Groupe quelconque

Classe d’un élément : on utilise les tables précédentes (figure 1).

Raisonnons sur un exemple (classe de \(D\)). Classe de D  \(\rightarrow\)   \(X^{-1}~D~X\) :

\[\begin{aligned} &X=E\qquad E^{-1}~D~E=D\qquad(\text{trivial})\\ &X=A\qquad A^{-1}~D~A=B~D~A=B~C=F\\ &\text{et ainsi de suite}\end{aligned}\]

3. Sous-groupe

3.1. Définition

Par définition, \(\Gamma\) est un sous-groupe de \(G\) si \(\{\gamma_1~,~\gamma_2\}\in~\Gamma\) et seulement si \(\gamma^{-1}\in~\Gamma\).

Ce qui veut dire que élément neutre \(\in~\Gamma\) : \[\gamma~\gamma^{-1}~\in~\Gamma~~~\text{ou}~~~e~\in~\Gamma\]

Un sous-groupe est en fait un groupe.

\(\{E,~A,~B\}\) forme un sous-groupe extrait du groupe précédent.

3.2. Groupe cyclique

Un groupe est cyclique si tous les éléments sont des puissances \(a^m\) de l’un d’entre eux.

Théorème

Dans un groupe fini \(G\), tout élément engendre un sous-groupe cyclique.

Suivant la table de multiplication précédente :

\[\begin{aligned} &~\forall~A\qquad~A^2=B\\ &\qquad\qquad A^3=B~A=E\end{aligned}\]

Le sous-groupe est donc \(\{E,~A,~B\}\).

On peut vérifier qu’il est cyclique. En effet, soient {\(a,~a^1,~a^2,~a^3,~\dots,~a^n\)}. Le groupe est fini, donc tous les éléments de la suite ne sont pas distincts.

Soit \((n+1)\) l’exposant du premier terme égal à un terme déjà obtenu :

\[\begin{aligned} a^{n+1}&=a^m\qquad m=1+m'\\ a^{n}&=a^{m'}\end{aligned}\]

Donc, \((n+1)\) ne serait pas le premier exposant. Donc, \(m=1\) et \(a^{n+1}=a\). On peut alors écrire : \[a^{-1}~a^{n+1}=a^{-1}~a\quad\Rightarrow\quad a^n=e\]

On a une suite périodique (\(n\) est appelé ordre de \(a\)).

4. Anneau

On appelle anneau un ensemble où sont définies deux opérations internes telles que :

1. la première loi notée \(\bigoplus\) lui donne une structure de groupe abélien (commutativité, associativité, élément neutre, inverse) ;

2. la deuxième loi notée \(\bigotimes\) est associative et distributive par rapport à la première.

Exemple 1 : ensemble \(\mathbb Z\) des entiers relatifs

Exemple 2 : ensemble \(K(x)\) des polynômes de la variable \(x\)

5. Corps

Un corps est un ensemble où sont définies deux opérations internes :

1. la première notée \([+]\) lui donne une structure de groupe abélien ;

2. la deuxième notée \([\times]\), distributive par rapport à la première lui donne une structure de groupe abélien, à ceci près que l’élément neutre de la première n’a pas d’inverse pour la deuxième.

Exemples

• Corps des rationnels \(\mathbb Q\). \([+]\) : addition  et  \([\times]\) : multiplication (\(0^{-1}\) n’existe pas) ;

• Corps des réels \(\mathbb R\),  des complexes \(\mathbb C\),  ensemble \(\mathbb Z\) ;

• \(K(x)\) n’est pas un corps, car \(\cfrac{1}{1+x}~\notin~K(x)\) ;

• Un quaternion est un corps non commutatif.