1. Intégration de l’équation de Bessel
1.1. Origine
La fonction de Bessel est fournie par la résolution de l’équation de Laplace en coordonnées cylindriques : \[\Delta U=\frac{\partial^2U}{\partial r^2}+\frac{1}{r}~\frac{\partial U}{\partial r}+\frac{1}{r}~\frac{\partial^2U}{\partial\theta^2}+\frac{\partial^2U}{\partial z^2}\]
On recherche une solution de la forme (séparation des variables) : \[U=R(r)~\Phi(\theta)~Z(z)\]
Effectuant ce changement et divisant par le produit \(R~\Phi~Z\), il vient : \[\frac{R''}{R}+\frac{1}{r}\frac{R'}{R}+\frac{1}{r^2}\frac{\Phi''}{\Phi}+\frac{Z''}{Z}=0\]
qui peut encore s’écrire : \[\frac{R''}{R}+\frac{1}{r}~\frac{R'}{R}+\frac{1}{r^2}~\frac{\Phi''}{\Phi}=-\frac{Z''}{Z}=\text{cte}\]
On peut écrire que : \[-\frac{Z''}{Z}=-k^2\quad\Rightarrow\quad x=A~\cosh(k~z+\mu)\]
On aurait pu faire de manière analogue : \[r^2~\Big(\frac{R''}{R}+\frac{1}{r}~\frac{R'}{R}+\frac{Z''}{Z}\Big)=-\frac{\Phi''}{\Phi}=\text{cte}\]
Et écrire que : \[\frac{\Phi''}{\Phi}=-\nu^2\quad\Rightarrow\quad\Phi=B~\sin(\nu~\theta+\lambda)\]
Il reste : \[R''+\frac{1}{r}~R'+(k^2-\frac{\nu^2}{r^2})~R=0\]
Posant alors \(R=y\) et \(x=k~r\), on obtient, tous calculs faits : \[y''+\frac{1}{x}~y'+\Big(1-\frac{\nu^2}{x^2}\Big)~y=0\qquad[1]\]
1.2. Solutions particulières
On recherche une solution de la forme : \[y=\sum_{\lambda=0}^{\lambda=\infty} a_{\lambda}~x^{r+\lambda}\quad;\quad a_0\neq 0\]
Il s’agit d’une série entière multipliée par une puissance (\(r\)) de \(x\).
Toutes substitutions faites et tous calculs faits, on aboutit à : \[(r^2-\nu^2)~a_0=0\qquad\text{donc :}\quad r=\pm~\nu\]
Deux solutions possibles : \[y=x^{~\pm~\nu}\sum_{\lambda=0}^{\lambda=\infty}a_{\lambda}~x^{\lambda}\]
1.2.1. Solution 1
Changement de variable : \[y=x^{\nu}~z\]
On est conduit à : \[x~z''+(2~\nu+1)~z'+x~z=0\qquad[2]\]
On peut encore trouver une solution particulière : \[z=\sum_{\lambda=0}^{\infty}a_{\lambda}~x^{\lambda}\quad;\quad a_0\neq~0\]
Tous calculs faits, on obtient la relation fondamentale : \[a_{\lambda}=-\frac{a_{\lambda-2}}{\lambda~(2~\nu+\lambda)}\qquad[3]\]
En exploitant cette récurrence et l’équation différentielle dont elle est issue, on démontre que les termes impaires \(a_{2p+1}\) sont nuls.
Les termes impairs ont pour expression : \[a_{2p}=(-1)^p~\frac{a_0}{2^{2p}~p!~(\nu+p)~(\nu+p-1)~\dots~(\nu+1)}\qquad[4]\]
Notant l’équivalence \(p!=\Gamma(p+1)\) et tous calculs faits, on écrit : \[y=J_{\nu}(x)=\sum_0^{\infty}(-1)^p~\frac{(x/2)^{2p+\nu}}{\Gamma(p+1)~\Gamma(\nu+p+1)}\qquad[5]\]
C’est la fonction de Bessel d’ordre \(\nu\).
1.2.2. Solution 2
Solution triviale \(J_{-\nu}\). Il suffit de changer \(\nu\) en \(-\nu\) dans l’expression de \(J_{\nu}\) précédente.
1.3. Graphes de \(J_0\) et \(J_1\)
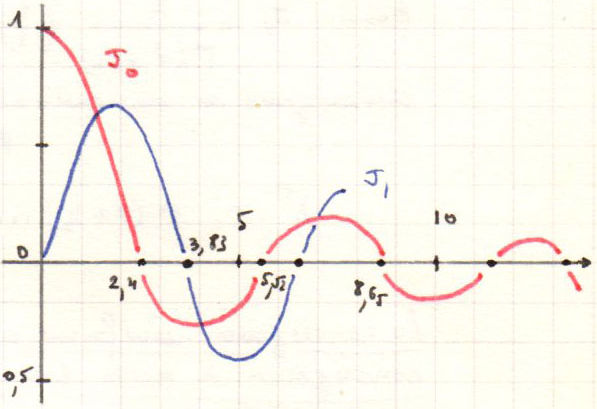 En se référant aux formules précédentes,
En se référant aux formules précédentes,
Fonction paire : \[J_0(x)=1-\frac{x^2}{2^2}~\frac{1}{1!~1!}+\frac{x^4}{2^4}~\frac{1}{2!~2!}+\dots\]
Fonction impaire : \[J_1(x)=\frac{x}{2}~\frac{1}{1!~1!}-\frac{x^3}{2^3}~\frac{1}{1!~2!}+\frac{x^5}{2^5}~\frac{1}{2!~3!}+\dots\]
Valeur asymptotique de \(J_n\) : \[n~~\rightarrow~~\infty\qquad~J_n\approx\sqrt{\frac{2}{\pi~x}}~\cos\Big\{x-(2~n+1)\frac{\pi}{4}\Big\}\qquad[6]\]
1.4. Solution générale
Dans le cas où \(\nu\) est non entier, on démontre qu’une solution de \([1]\) est de la forme : \[y=A~J_{\nu}-B~J_{-\nu}\]
Dans le cas où \(\nu\) entier, on démontre que la solution générale est de la forme : \[y=A~J_{\nu}+B~N_{\nu}\qquad\text{avec~:}\quad N_{\nu}=\frac{J_{\nu}~\cos(\pi~\nu)-J_{-\nu}}{\sin(\pi~\nu)}\qquad[7]\]
\(N_{\nu}\) est la fonction de Neumann.
On notera que, dans le cas entier : \[J_{-n}=(-1)^n~J_{n}\]
2. Récurrence et intégrales pour \(\nu\) quelconque
2.1. Récurrences
Partant de la relation \([5]\) : \[y=J_{\nu}(x)=\sum_0^{\infty}(-1)^p~\frac{(x/2)^{2p+\nu}}{\Gamma(p+1)~\Gamma(\nu+p+1)}\]
et, opérant une suite de dérivations, on obtient trois relations de récurrence importantes : \[\begin{aligned} x~J'_{\nu}&=\nu~J_{\nu}-x~J_{\nu+1} &&(a)\\ J'_{\nu}&=-\frac{\nu}{x}~J_{\nu}+J_{\nu-1} &&(b)\\ J_{\nu}&=(J_{\nu-1}+J_{\nu+1})~\frac{x}{2~\nu}\qquad &&(c) \end{aligned} \quad[8]\]
2.2. Intégrales
On part de deux relations :
– la fonction \(\beta\) qui est déjà connue sous forme intégrale (voir fonctions eulériennes) : \[\beta(p,~q)=2~\int_0^{\pi/2}\cos^{2p-1}\theta~\sin^{2q-1}\theta~d\theta\]
– l’expression de \(J_{\nu}\) reformulée pour le calcul à suivre : \[J_{\nu}=\Big(\frac{x}{2}\Big)^{\nu}~\sum_{r=0}^{\infty}(-1)^r~\frac{(x/2)^{2r}}{r!~\Gamma(r+\nu+1)}\]
Introduisant de plus le changement de variable \(\cos\theta=t\), on obtient la formule générale : \[J_{\nu}=\Big(\frac{x}{2}\Big)^{\nu}~\frac{1}{\sqrt{\pi}}~\frac{2}{\Gamma(\nu+1/2)}~\int_0^1\cos(x~t)~(1-t^2)^{\nu-1/2}~dt\qquad[9]\]
En particulier : \[\begin{aligned} &J_0=\frac{2}{\pi}\int_0^1\frac{\cos(x~t)}{\sqrt{1-t^2}}~dt\\ &J_1=\frac{2x}{\pi}\int_0^1\cos(x~t)~\sqrt{1-t^2}~dt \end{aligned} \qquad[10]\]
3. Fonctions de Bessel pour n entier et 1/2 entier
3.1. Fonction génératrice
On considère la fonction : \[G(x,u)=e^{x/2(u-1/u)}\]
Elle présente un point singulier pour \(u=0\). Pour tout \(x\) fixe, \(G\) est holomorphe dans le plan complexe, sauf en \(u=0\).
En effectuant le développement de la fonction exponentielle \(G\), on obtient : \[G(x,~u)=e^{x/2(u-1/u)}=\sum_{n=-\infty}^{\infty}J_n(x)~u^n\qquad[11]\]
Si l’on fait le développement de Laurent de \(G\) autour de l’origine dans le plan complexe, les \(J_n~u^n\) en sont les coefficients.
3.2. Intégrales \(J_{1/2}\) , \(J_{-1/2}\)
On part toujours du développement de l’expression de \(J_{\nu}\).
Tous calculs faits, on obtient pour les deux premières : \[J_{1/2}=\sqrt{\frac{2}{\pi~x}}~\sin x\quad;\quad J_{-1/2}=\sqrt{\frac{2}{\pi~x}}~\cos x\qquad[12]\]
Pour les demi-entiers supérieurs, on mettra à profit la relation : \[\frac{2\nu}{x}~J_{\nu}=J_{\nu-1}+J_{\nu+1}\]
Ainsi, pour \(\nu=1/2\), on aura : \[\frac{1}{x}~J_{1/2}=J_{-1/2}+J_{3/2}\]
et ainsi de suite.
On a donc :
\[\begin{aligned} &J_{3/2}=\sqrt{\frac{2}{\pi~x}}~\Big(\frac{\sin x}{x}-\cos x\Big)\\ &J_{-3/2}=-\sqrt{\frac{2}{\pi~x}}~\Big(\frac{\cos x}{x}+\sin x\Big)\end{aligned}\]

