1. Notion de série statistique
Si les éléments d’un même ensemble présentent tous un caractère commun dont on peut apprécier l’importance et si l’on repère celle-ci pour chaque élément de l’ensemble, l’ensemble des couples « élément – importance du caractère » constitue une série statistique.
Nous examinons dans ce chapitre les divers modes de représentation de la série.
2. Représentation de la série statistique
Ces divers types de représentation seront mis en évidence par des exemples pour mieux fixer les idées.
2.1. Représentation par tableau
\[\begin{matrix} \text{Option} &\text{Index} &\text{Effectif} &\text{Répartition}\\ \hline \text{Transmission} &1 &20 &17.24\\ \text{Commutation} &2 &25 &21.55\\ \text{Résaux} &3 &35 &30.18\\ \text{Robotique} &4 &14 &12.5\\ \text{Télématique} &5 &22 &18.98 \end{matrix}\]
2.2. Diagramme en bâtons
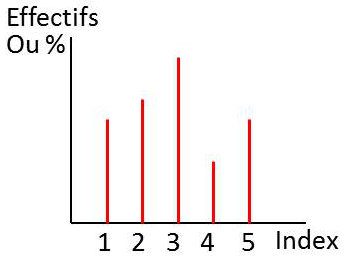Le diagramme en bâtons correspond à une représentation classique.
Les représentations par effectifs ou par pourcentages sont identiques. Ils ne différent que par un changement d’échelle sur l’axe des ordonnées.
2.3. Histogramme
Un exemple :
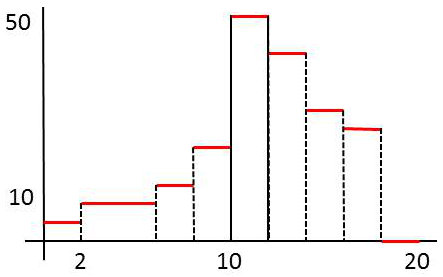
Distribution des notes d’examen, notation \(x\in 0~,~20\) dans une promotion de 180 élèves.
On a regroupe les notes par sous ensemble (suivant un tableau) et représenté l’histogramme correspondant. \[\begin{matrix} \text{Note} &\text{Nbre d'élèves}\\ \hline 0\leq x\leq 2 &2\\ 2\leq x\leq 4 &6\\ 4\leq x\leq 6 &6\\ 6\leq x\leq 8 &8\\ 8\leq x\leq 10 &22\\ 10\leq x\leq 12 &54\\ 12\leq x\leq 14 &42\\ 14\leq x\leq 16 &24\\ 16\leq x\leq 18 &16\\ 18\leq x\leq 20 &0 \end{matrix}\]
2.4. Polygones des effectifs et des effectifs cumulés
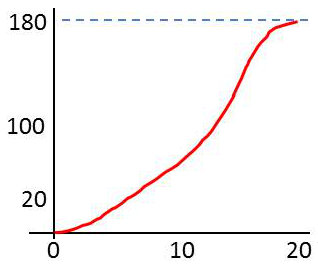En joignant les centres des segments ordonnées de l’histogramme précédent, on obtient une ligne brisée appelée polygone des effectifs. \[\begin{matrix} \text{Note} &\text{Cumul d'élèves}\\ \hline 0 &0\\ 2 &2\\ 4 &8\\ 6 &14\\ 8 &22\\ 10 &44\\ 12 &98\\ 14 &140\\ 16 &164\\ 18 &180\\ 20 &180 \end{matrix}\]
La forme présente une certaine analogie avec la fonction de répartition du calcul des probabilités.
Le graphe représente les ensembles de notes telles que \(n_1<2\) ; \(n_2<4\) ; \(n_3<8\) ; etc.
