1. Généralités

L’échantillonnage idéal à la fréquence \(f_e=1/T_e\) d’un signal continu \(x(t)\) fournit le signal : \[\tilde{x}=\sum_{k=-\infty}^{+\infty}x(k~T_e)~\delta(t-k~T_e)\]

qui est encore un signal à temps continu.

Si l’on ne s’intéresse qu’aux seules valeurs prises par le signal \(x(t)\) aux instants significatifs \(k~T_e\), on sera amené à ne considérer que la suite des amplitudes des échantillons, c’est-à-dire la suite numérique des \(x(k~T_e)\).

Cette suite de nombres peut s’écrire plus simplement \(\{x(k),~k\in Z\}\) après avoir normalisé le temps en posant \(T_e~;~f_e=1\). Le temps représenté par la variable \(k\in Z\) a été discrétisé.

Cet exemple, emprunté à la théorie du signal, montre une origine ou une interprétation possible des signaux à temps discret, mais ce n’est pas la seule. D’une façon plus générale, un signal à temps discret est une suite de nombres (réels ou complexes).

1.1. Exemples de signaux à temps discret

Impulsion unité \[\delta=\left\{ \begin{aligned} &1\qquad k=0\\ &0\qquad\text{sinon} \end{aligned} \right.\]

À ne surtout pas confondre avec l’impulsion de Dirac.

Échelon unité \[u(k)=\left\{ \begin{aligned} &1\qquad k\geq 0\\ &0\qquad k<0 \end{aligned} \right.\]

Porte de longueur N \[\Pi_N(k)=\left\{ \begin{aligned} &1\qquad 0\leq k\leq N-1\\ &0\qquad\text{sinon} \end{aligned} \right.\]

On peut transposer aux signaux à temps discret les principaux concepts définis pour les signaux à temps continu.

1.2. Principaux concepts

Périodicité

\(x(t)\) est périodique \(N\) si \(N\) est le plus petit entier tel que : \[x(k+N)=x(k)\qquad\forall~k\in Z\]

Énergie \[E=\sum_{k=-\infty}^{+\infty}\big|x(k)\big|^2\]

Puissance \[P=lim_{~N~\rightarrow~\infty}~\frac{1}{2~N+1}\sum_{k=-\infty}^{+\infty}\big|x(k)\big|^2\]

1.3. Principales opérations

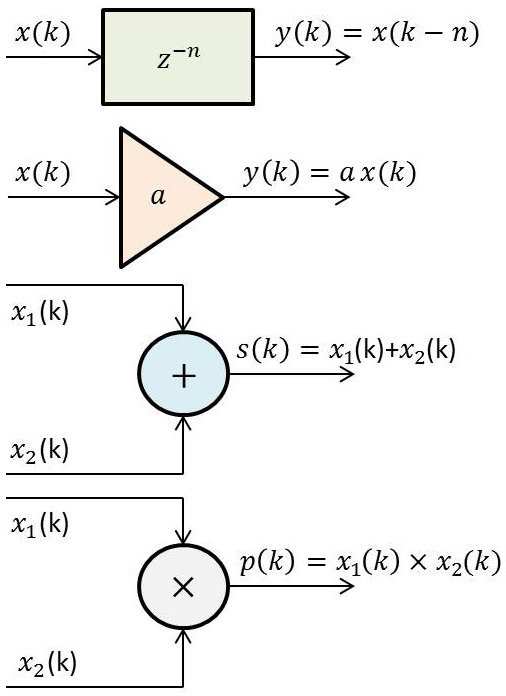
On peut appliquer aux signaux à temps discret des opérations de décalage temporel, de multiplication par un scalaire, de somme, de produit et de convolution.

Les symboles de ces quatre opérations sont représentées dans l’ordre respectif à la figure ci-contre.

Le produit de convolution : \[\begin{aligned} &z(k)=x(k)\star y(k)=\sum_{k=-\infty}^{+\infty} x(n)~y(k-n)\\ &z(k)=\sum_{k=-\infty}^{+\infty} y(n)~x(k-n)\end{aligned}\] apparaît alors comme une combinaison des opérations précédentes.

Remarque

L’impulsion unité permet de décomposer tout signal sous forme d’une combinaison linéaire de signaux \(\delta(k-n)\) : \[x(k)=\sum_{n=-\infty}^{+\infty} x(n)~\delta(k-n)=x(k)\star \delta(k)\]

2. Transformation en Z et transformée de Fourier

2.1. Transformée en Z

À tout signal \(x(k)\), on peut associer de façon formelle une transformée en Z, notée \(X(z)\) par : \[X(z)=\sum_{k=-\infty}^{+\infty} x(k)~z^{-k}\qquad k\in\mathbb{C}\]

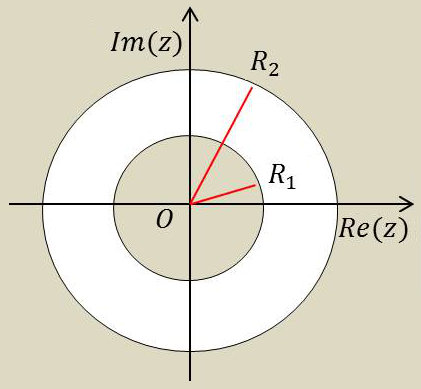
Il s’agit d’une série de Laurent qui ne peut être interprétée comme une fonction de la variable complexe \(z\) que si l’on précise le domaine de convergence de cette série.

Dans le plan complexe le domaine de convergence de ce type de série est un disque ouvert \((R_1<~|z|<R_2)\).

Le domaine de convergence de la série fait partie intégrante de la définition de la transformée en \(z\), car une expression peut être transformée en \(z\) de plusieurs signaux différents si on ne précise pas le domaine de convergence comme le montre l’exemple ci-dessous.

Soient les signaux : \[\begin{aligned} &x_1(k)=a^k~u(k)\\ &x_2(k)=-a^k~u(-k-1) \end{aligned} \qquad\qquad\\ 0<a<1\]

Calculons leur transformée en \(z\). La première est classique : \[X_1(z)=\sum_{k=0}^{+\infty} a^k~z^{-k}=\frac{1}{1-a~z^{-1}}\qquad\qquad |z|<a\]

La deuxième est établie par étapes : \[\begin{aligned} &X_2(z)=-\sum_{k=-\infty}^{-1} a^k~z^{-k}=-\sum_{k=1}^{+\infty} a^{-k}~z^k=-a^{-1}~z\sum_{k=0}^{+\infty}a^{-k}~z^k\\ &X_2(z)=-\frac{a^{-1}~z}{1-z/a}=\frac{1}{1-a~z^{-1}}\qquad\qquad |z|>a\end{aligned}\]

Ainsi, \(x_1(k)\) et \(x_2(k)\) sont donc deux signaux différents admettant des transformées en \(z\) ayant même expression, mais sur des domaines différents. Le premier sera dit causal et le deuxième anti-causal.

2.1.1. Théorème du retard

Formulation : \[y(k)=x(k-n)\qquad\Rightarrow\qquad Y(z)=z^{-n}~X(z)\]

Le calcul est facile : \[Y(z)=\sum_{k=-\infty}^{+\infty} y(k)~z^{-k}=\sum_{k=-\infty}^{+\infty} x(k-n)~z^{-k}=\sum_{l=-\infty}^{+\infty}x(l)~z^{-l-n}=~\dots\]

2.1.2. Théorème relatif au produit de convolution

Soient les signaux : \[\begin{aligned} x(k)\xrightarrow[]{TZ}X(z)\qquad&\text{sur}\quad D_x\\ y(k)\xrightarrow[]{TZ}Y(z)\qquad&\text{sur}\quad D_y\end{aligned}\]

et soit : \[w(k)=x(k)\star y(k)=\sum_{n=-\infty}^{+\infty} x(k-n)~y(n)\qquad\text{sur}\quad D_x\cap D_y\]

Alors : \[X(z)~Y(z)=\sum_{m=-\infty}^{+\infty} x(m)~z^{-m}\sum_{n=-\infty}^{+\infty} y(n)~z^{-n}=\sum_m\sum_n x(m)~y(n)~z^{-(m+n)}\]

Soit : \[X(z)~Y(z)=\sum_k\sum_n x(k-n)~y(n)~z^{-k}\]

On a donc : \[x(k)\star y(k)\xrightarrow[]{TZ}X(z)~Y(z)\]

2.1.3. Inversion de la transformée en Z

Nous savons que toute fonction holomorphe \(X(z)\) définie dans un disque ouvert \(D=R_1<~|z|<R_2\) peut être développée en série de Laurent sous la forme : \[X(z)=\sum_{k=-\infty}^{+\infty} x(k)~z^{-k}\]

Le problème de l’inversion de la transformée en \(Z\) consiste à déterminer \(x(k)\) pour tout \(k\in Z\) à partir de \(X(z)\). La réponse générale à ce problème est fournie par la formule de Cauchy : \[x(k)=\frac{1}{2~i~\pi}\int_C X(z)~z^{k-1}~dz\qquad\forall~k\in Z\]

\(C\) est un chemin quelconque, inclus dans \(D\), entourant l’origine et parcouru dans le sens direct. Le calcul pratique de \(x(k)\) peut se faire en appliquant cette formule et en utilisant le théorème des résidus.

Toutefois, lorsque \(X(z)\) se présente sous la forme particulière d’une fraction rationnelle en \(z\), la méthode précédente pourra avantageusement être remplacée par une méthode reposant sur le principe d’une décomposition de la fraction rationnelle en éléments simples.

2.1.4. Transformée de Fourier

La transformée de Fourier est donnée par : \[X(f)=\sum_{k=-\inf}^{+\infty} x(k)~\exp(-j~2\pi~k~f)\]

On remarque que cette transformée de Fourier est égale à la transformée en \(z\) évaluée sur le cercle unité. En conséquence, la transformée de Fourier d’un signal n’est définie que si le cercle unité appartient au domaine de convergence de la transformée en \(z\) de ce signal.

\(X(f)\) est périodique de période 1. En effet : \[\exp[-j~2\pi~k~(f+1)]=\exp(-j~2\pi~k~f)\qquad\text{car :}\quad\exp(-j~2\pi~k)=1\]

Il s’ensuit que \(X(f)\) l’est également. On peut donc restreindre l’étude de \(X(f)\) à l’intervalle \([-1/2,~+1/2]\) appelé intervalle principal.

Remarque

Si le signal à temps discret provient de l’échantillonnage d’un signal à temps continu, il est bon de se souvenir que la fréquence a été normalisée en posant \(f_e=1\).

D’autre part, la formule de définition de la transformée n’est autre que la décomposition en série de Fourier de la fonction périodique \(X(f)\), les \(x(k)\) apparaissent alors comme les coefficients de cette décomposition. De ce fait : \[x(k)=\int_{-1/2}^{+1/2} X(f)\exp(j~2\pi~k~f)~df\]

La transformée de Fourier d’un signal à temps discret jouit des mêmes propriétés que la transformée de Fourier d’un signal à temps continu.

En particulier :

1) Si \(x(k)\) est réel, \(X(f)\) est à symétrie hermitienne : \[X(-f)=\overline{X(f)}\]

On peut alors restreindre le domaine d’étude à l’intervalle \([0,~+1/2]\).

2) Théorème du retard : \[x(k-n)\xrightarrow[]{TF} X(f)~\exp(-j~2\pi~n~f)\]

Prenons un exemple pour fixer les idées.

Soit le signal \(x(k)=\Pi_N(k)\). Il a pour transformée de Fourier : \[X(f)=\sum_{k=0}^{N-1} \exp(-j~2\pi~k~f)=\frac{1-\exp(-j~2\pi~N~f)}{1-\exp(-j~2\pi~f)}=\frac{\sin(\pi~N~f)}{\sin(\pi~f)}~\exp[-j~\pi~(N-1)~f]\]

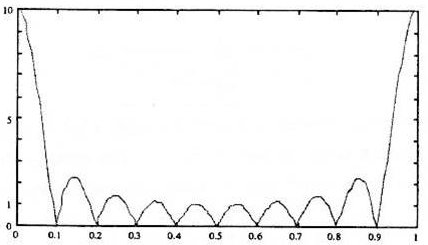
Ou encore : \[X(f)=\frac{\sin(\pi~N~f)}{\sin(\pi~f)}~\exp[-j~\pi~(N-1)~f]\]

La figure ci-contre représente le spectre associé à \(X(f)={\rm TF}\big\{\Pi_N(k)\big\}\) dans le cas où \(N=10\).