1. Définitions et formules générales
1.1. Équilibre des charges sur les conducteurs
Dans les conducteurs, chaque atome de la matière qui constitue le corps a perdu un ou plusieurs électrons. Un véritable gaz électronique circule autour des noyaux, de manière désordonnée.
Les propriétés des conducteurs en équilibre s’expliquent en admettant que ces électrons circulent librement à l’intérieur du corps, aucune force en moyenne n’agissant sur eux. Ces électrons ne peuvent quitter le corps à travers la surface. Il faut donc admettre que, sur cette dernière, il y a brusquement des forces qui les renvoient vers l’intérieur.
C’est lorsque la température s’élève ou quand des champs intenses sont réalisés à froid sur cette surface que l’on arrive à extraire des électrons du métal.
L’équilibre d’un conducteur isolé dans l’espace et qui n’est soumis à aucune action extérieure se traduit par \(\overrightarrow{E}=\overrightarrow{0}\), partout à l’intérieur, sauf sur la surface. Si tel n’était pas le cas, une force moyenne \(\overrightarrow{f}=q~\overrightarrow{E}\) agirait sur les électrons et ceux-ci se déplaceraient.
Rappelons que : \[\begin{aligned} \rm div(\overrightarrow{E})&=\rho\\ \overrightarrow{E}&=\overrightarrow{0}\quad\Rightarrow\quad\rho=0\quad\text{partout à l’intérieur} \end{aligned} \qquad[1]\]
Cela signifie que, dans chaque élément de volume, il y a autant de charges positives que de charges négatives. Ainsi, la charge d’un conducteur ne peut être que superficielle et le champ produit par cette distribution est nul en tout point intérieur.
Considérons maintenant un conducteur isolé, ne portant aucune charge, placé dans un champ fixe \(\overrightarrow{E_0}\). On étudie le processus par lequel il va parvenir à un état d’équilibre.
Les électrons intérieurs étant soumis à un champ \(\overrightarrow{E}\) vont se déplacer jusqu’aux limites qui leur sont assignées : la surface. Ils vont s’y accumuler et le mouvement cessera quand le champ produit par ces charges superficielles sera exactement égal et opposé à l’intérieur au champ \(\overrightarrow{E_0}\). À ce moment, le conducteur aura atteint son état d’équilibre. Le champ total à l’intérieur est donc nul et l’on a \(\rho=0\) ; les charges sont donc encore purement superficielles.
Nous admettons donc qu’un conducteur est un réservoir inépuisable d’électrons.
On pourrait imaginer le cas où tous les électrons auraient été extraits de l’intérieur : les propriétés du conducteur seraient alors tout à fait différentes et ressembleraient à celles des diélectriques qui seront étudiés plus loin avec en plus une charge superficielle réelle.
Quand le conducteur est initialement neutre et isolé, il y a autant de charges négatives que de charges positives sur la surface. En définitive, tout se passe comme si certaines parties de la surface s’appauvrissaient en électrons pour devenir positives tandis que d’autres parties s’enrichiraient en électrons pour devenir négatives.
Quelles que soient les conditions dans lesquelles est placé le conducteur, on a toujours : \[\overrightarrow{E}=\overrightarrow{0}~~~\text{partout à l'intérieur}~~=~~\text{condition d'équilibre}\]
Il en résulte que le potentiel est constant en tout point du volume et, comme il est continu, il est aussi constant sur la surface. Les surfaces des conducteurs en équilibre sont donc des surfaces équipotentielles.
Les lignes de force étant normales aux surfaces équipotentielles, le champ électrique est normal au voisinage immédiat de la surface d’un conducteur.
\(\sigma\) étant la densité superficielle de charge : \[E_t=0\quad;\quad E_{ext}-E_{int}=\frac{\sigma}{\varepsilon_0}\qquad[2]\]
On a ici : \[E_{int}=0\quad\Rightarrow\quad E_{ext}=\frac{\sigma}{\varepsilon_0}\qquad[3]\]
Or, le champ est discontinu sur la surface. On aura donc (chapitre précédent) : \[E_S=\frac{1}{2}~(E_{int}+E_{ext})=\frac{\sigma}{\varepsilon_0}\qquad[4]\]
Il vient alors : \[E_{ext}=\frac{\sigma}{\varepsilon_0}\quad\Rightarrow\quad\sigma=\varepsilon_0~E=-\varepsilon_0~\frac{\partial V}{\partial n}\qquad[5]\]
\(\partial/\partial n\) dérivée suivant la normale extérieure à la surface du conducteur.
1.2. Problèmes relatifs aux conducteurs
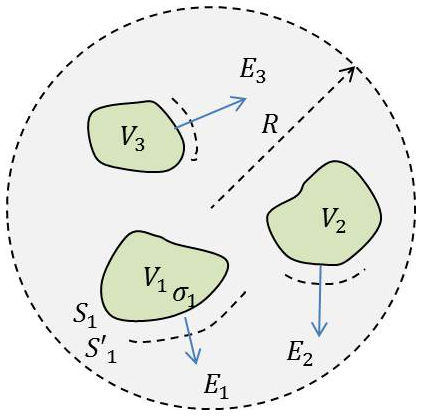 Soient plusieurs conducteurs isolés dans l’espace et limités par des surfaces \(S_1,~S_2,~S_3\), etc. Nous supposons de plus que chacun d’eux occupe un volume fini et qu’ils sont à des distances finies les uns des autres. Il en résulte que l’on peut tracer une sphère ayant l’origine pour centre et qui les engloberait tous.
Soient plusieurs conducteurs isolés dans l’espace et limités par des surfaces \(S_1,~S_2,~S_3\), etc. Nous supposons de plus que chacun d’eux occupe un volume fini et qu’ils sont à des distances finies les uns des autres. Il en résulte que l’on peut tracer une sphère ayant l’origine pour centre et qui les engloberait tous.
Si on connaît la densité superficielle de charge sur tous les conducteurs, on en déduit le potentiel en tout point de l’espace par l’expression : \[V=\frac{1}{4\pi~\varepsilon_0}\int_{S_1+S_2+\dots}\frac{\sigma}{r}~ds\qquad[6]\]
Des potentiels, on déduit les champs par dérivation. Inversement, si l’on se donne la valeur des potentiels sur chacun des conducteurs, on démontre que le potentiel est de ce fait déterminé dans tout l’espace.
En général, on ne connaît pas à priori la répartition des charges sur les conducteurs. On se donne soit le potentiel des conducteurs, soit leur charge totale \(Q\). On dira par exemple que l’un des conducteurs est isolé et primitivement neutre, (\(Q=0\)).
Quand on a un système de conducteurs chargés à distance finie, on peut choisir \(V=0\) à l’infini. On peut aussi faire \(V=0\) sur l’un quelconque des conducteurs à condition toutefois que son potentiel reste constant.
Comme on opère toujours à la surface de la Terre et qu’elle peut être considérée comme un conducteur, on a l’habitude de prendre \(V=0\) pour le potentiel du sol. En toute rigueur, on n’est sûr de la constance de \(V\) qu’à l’infini, mais pratiquement on peut, dans tous les problèmes qui se posent à la surface de la Terre, faire \(V=0\) pour la surface du sol.
En résumé, les problèmes les plus généraux qui se posent relativement aux conducteurs d’un système sont du type suivant :
-
on connaît le potentiel de certains conducteurs (reliés aux bornes de générateurs) ;
-
on connaît les charges totales de certains conducteurs parce qu’ils sont isolés.
Il faut alors chercher une solution :
-
qui obéisse à l’équation de Laplace à l’extérieur de tous les conducteurs,
-
qui se réduise à une constante sur chacun d’eux,
-
qui soit telle que sur les conducteurs dont la charge totale est connue on ait : \[\int_S\frac{\partial V}{\partial n}~ds=-\frac{Q}{\varepsilon_0}\qquad[7]\]
-
et qui s’annule à l’infini comme [\(Q/R\)] sauf si toutefois la charge totale du système est nulle auquel cas elle s’annulerait à l’infini comme [\(Q/R^2\)].
Une fois que l’on a trouvé un potentiel qui satisfasse à toutes ces conditions, on en déduit les champs par dérivation e, en particulier, on a la valeur des densités superficielles au moyen de la formule : \[\sigma=\varepsilon_0~E=-\varepsilon_0~\frac{\partial V}{\partial n}\qquad[8]\]
1.3. Distribution des lignes de champ
Les lignes de champ sont tangentes en chaque point au vecteur champ. Elles vont des charges positives aux charges négatives.
À la surface des conducteurs : \[E_{n,~vide}=\frac{\sigma}{\varepsilon_0}\qquad[9]\]
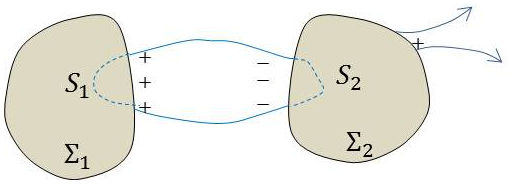 Les tubes de champ sont constitués par les lignes de champ passant par un contour fermé.
Les tubes de champ sont constitués par les lignes de champ passant par un contour fermé.
Le théorème des éléments correspondants se démontre pour les tubes vides de charges à l’aide du théorème de Gauss appliqué au tube lui-même et à deux surfaces terminales tracées dans les conducteurs.
Le flux total à travers cette surface est nul puisque \(\overrightarrow{E}\) est nul sur \(\Sigma_1\) et \(\Sigma_2\) et qu’il est tangent aux parois du tube de force.
Les charges terminales sont opposées ; on les dit correspondantes.
Dans le cas général d’un tube à deux extrémités, on a : \[\sigma_1~S_1=\sigma_2~S_2\qquad[10]\]
Les lignes de champ sont d’autant plus resserrées que \(\sigma\) est grand.
Deux conducteurs sont en influence partielle si une partie des lignes de champ issues de l’un atteint l’autre. L’influence est totale entre un conducteur et une enceinte fermée qui l’entoure : les charges en regard sont alors égales et opposées. L’influence est nulle entre deux conducteurs séparés par un écran mis à la terre.
1.4. Relations entre charges et potentiels d’un système de conducteurs
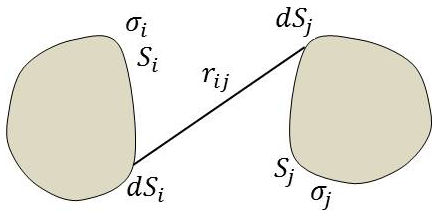 Soit un système de \(k\) conducteurs en équilibre électrostatique, limités par les surfaces \(S_1,~S_2,~\dots,~S_k\) et ayant des densités superficielles respectivement égales à \(\sigma_1,~\sigma_2,~\dots,~\sigma_k\).
Soit un système de \(k\) conducteurs en équilibre électrostatique, limités par les surfaces \(S_1,~S_2,~\dots,~S_k\) et ayant des densités superficielles respectivement égales à \(\sigma_1,~\sigma_2,~\dots,~\sigma_k\).
Le potentiel \(V_i\) en un point quelconque \((x_i,~y_i,~z_i)\) de la surface du \(i^{\text{ème}}\) conducteur est : \[V_i=\frac{1}{4\pi~\varepsilon_0}~\sum_{j=1}^{j=k}\int_{S_j}\frac{\sigma_j}{r_{ij}}~dS_j\qquad[11]\]
\(r_{ij}\) désigne la distance de l’élément de surface \(dS_j\) du \(j^{\text{ème}}\) conducteur au point \((x_i,~y_i,~z_i)\).
Multiplions les deux membres de la relation par \(\sigma_i\) et intégrons sur toute la surface du \(i^{\text{ème}}\) conducteur. Au premier membre, \(V_i\) étant constant sur toute la surface peut sortir de l’intégrale qui est alors égale à la charge totale \(Q_i\) de ce conducteur. On obtient alors : \[V_i=\frac{1}{4\pi~\varepsilon_0~Q_i}~\sum_{j=1}^{j=k}\int_{S_i}\int_{S_j}\frac{\sigma_i~\sigma_j}{r_{ij}}~ds_i~ds_j\qquad[12]\]
Posons : \[p_{ij}=\frac{1}{4\pi\varepsilon_0Q_iQ_j}\sum_{j=1}^{j=k}\int_{S_i}\int_{S_j}\frac{\sigma_i~\sigma_j}{r_{ij}}~ds_i~ds_j\qquad[13]\]
Le potentiel \(V_i\) prend alors la forme : \[V_i=\sum_{j=1}^{j=k}p_{ij}~Q_j\qquad k\text{ équations analogues}\quad;\quad i=1,~2,~\dots,~k\qquad[14]\]
On voit sur la formule que les coefficients \(p_{ij}\) sont symétriques (\(p_{ij}=p_{ji}\)). Il est aussi facile de vérifier qu’ils ne dépendent pas de l’état électrique, mais uniquement de la configuration géométrique du système. En effet, si toutes les densités deviennent \(n\) fois plus grandes, les charges totales \(Q\) deviennent aussi \(n\) fois plus grandes et par conséquent les \(p_{ij}\) restent les mêmes. Ces coefficients sont les coefficients de potentiel ou élastances.
La formule montre que les \(V_i\) sont des combinaisons linéaires à coefficients constants des charges \(Q_i\) tant que la configuration du système reste inchangée.
On peut trouver une signification physique à ces coefficients. Si tous les \(Q\) sont nuls sauf \(Q_i=1\), on a alors d’après la relation précédente \(V_i=p_{ij}\). Donc \(p_{ij}\) est le potentiel auquel serait porté le \(i^{\text{ème}}\) conducteur si on plaçait la charge (\(+1\)) sur le \(j^{\text{ème}}\), tous les autres conducteurs ayant des charges nulles.
1.5. Coefficients de capacité et coefficients d’influence
Reprenant la relation : \[V_i=\sum_{j=1}^{j=k}p_{ij}~Q_j\qquad[15]\]
Il vient : \[Q_i=\sum_{j=1}^{j=k}C_{ij}~V_j\qquad[16]\]
avec : \[C_{ij}=\frac{P_{ij}}{\Delta}=\frac{\rm mineur[p_{ij}]}{\text{déterm}[p_{ij}]}\qquad[17]\]
Les \(P_{ij}\) sont symétriques, car les \(p_{ij}\) le sont et par conséquent les \(C_{ij}\), soit \(C_{ji}=C_{ij}\).
Un coefficient tel que \(C_{ii}\) où les deux indices sont égaux s’appelle la capacité du conducteur \(i\) en présence de tous les autres ; cette capacité est évidemment différente de la capacité du même conducteur isolé dans l’espace.
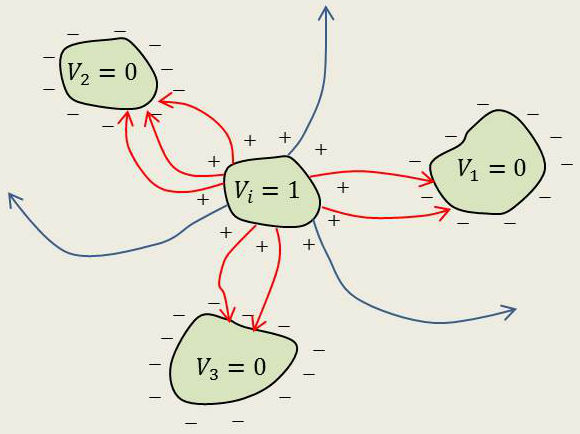 Montrons que tous les coefficients de capacité sont positifs tandis que les coefficients d’influence sont toujours négatifs. On considère pour cela l’état d’équilibre :
Montrons que tous les coefficients de capacité sont positifs tandis que les coefficients d’influence sont toujours négatifs. On considère pour cela l’état d’équilibre :
\[\begin{aligned} 0,~0,~\dots,~V_i&=1,~\dots,~0 \\ C_{1i},~C_{2i},~\dots,~&C_{ii},~\dots,~C_{ki}\end{aligned}\]
Les lignes de force partent du conducteur \(i\) qui est le seul à avoir un potentiel supérieur à zéro. Elles aboutissent aux autres conducteurs ou s’éloignent indéfiniment. Donc le conducteur \(i\) est chargé positivement et tous les autres négativement donc : \[C_{ii}>0\quad;\quad C_{ij}<0\qquad[18]\]
D’après le théorème des états correspondants la somme des charges négatives de tous les conducteurs influencés est plus petite que la charge du conducteur \(i\), d’où : \[C_{ii}~\geq~-\sum_{j\neq i}C_{ij}\qquad[19]\]
L’égalité correspondrait à un conducteur qui entourerait entièrement le conducteur \(i\), c’est-à-dire à l’influence totale.
1.6. Identité de Gauss
Soit \(S\) l’ensemble des surfaces qui limitent des conducteurs en équilibre électrostatique. Si nous considérons deux états d’équilibre caractérisés par \((\sigma,~V)\) et \((\sigma',~V')\) en chaque point de la surface, on a : \[\int_S V'~\sigma~dS~\equiv~\int_{S} V~\sigma'~dS'\qquad[20]\]
Pour démontrer cette proposition, il suffit de remplacer \(V\) et\(V'\) par leurs expressions : \[V=\frac{1}{4\pi~\varepsilon_0}\int_S\frac{\sigma}{r}~dS\quad;\quad V'=\frac{1}{4\pi~\varepsilon_0}\int_{S}\frac{\sigma'}{r'}~dS'\qquad[21]\]
Ce qui donne bien une identité.
Comme la surface \(S\) est l’ensemble des surfaces de plusieurs conducteurs, on a : \[S=\sum_iS_i\quad;\quad \sum_{S_i}\int_{S_i}V'_i~\sigma_i~ds_i=\sum_{S_i}\int_{S_i}V_i~\sigma'_i~ds'_i\qquad[22]\]
Comme les deux potentiels sont constants sur toute la surface d’un conducteur, on peut les faire sortir du signe intégration. Il reste alors des intégrales qui sont les charges totales \(Q_i\) et \(Q'_i\) des conducteurs, d’où la forme suivante : \[\sum_iQ_i~V'_i=\sum_iQ'_i~V_i\qquad[23]\]
C’est ce que l’on appelle l’identité de Gauss.
2. Conducteur unique isolé dans l’espace
2.1. Distribution des charges et capacités
On se donne la charge totale \(Q\) et il faut chercher la densité de charge en tout point de la surface du conducteur.
La méthode la plus simple et la plus utilisée consiste à chercher une solution de l’équation de Laplace qui se réduise à une constante sur le conducteur et s’annule à l’infini comme \(1/R\). On en déduit ensuite \(\sigma\) en appliquant la formule : \[\sigma=\varepsilon_0~E=-\varepsilon_0~\frac{\partial V}{\partial n}\qquad[24]\]
On multiplie \(\sigma\) par une constante convenable : \[\int\sigma~ds=Q\qquad[25]\]
pour que la fonction \(V\) se comporte comme \(Q/R\) à l’infini.
La formule : \[V=\frac{1}{4\pi~\varepsilon_0}~\int_S\frac{\sigma}{r}~dS\qquad[26]\]
montre que, si l’on a trouvé une solution du problème pour une valeur de \(Q\), la solution pour \(Q'=k~Q\) est \(k~\sigma\) et le potentiel correspondant est \(k~V\). Il y a donc un rapport constant entre \(Q\) et \(V_S\) pour un conducteur. Ce rapport est naturellement la capacité \(C\) : \[Q=C~V_S\qquad[27]\]
2.2. Cas de la sphère
Dans le cas de la sphère, par raison de symétrie, la densité doit être constante sur toute celle-ci.
Nous avons vu qu’une telle distribution produisait un champ nul à l’intérieur, ce qui constitue la condition d’équilibre du conducteur.
À l’extérieur, le potentiel est le même que si toute la charge était contenue au centre : \[V=\frac{Q}{4\pi~\varepsilon_0}~\frac{1}{R}\qquad[28]\]
En particulier : \[V=a\quad;\quad Q=4\pi~\varepsilon_0~a~V_S\qquad[29]\]
D’où l’expression de la capacité de la sphère : \[C=4\pi~\varepsilon_0~a\qquad[30]\]
3. Condensateurs
3.1. Influence totale
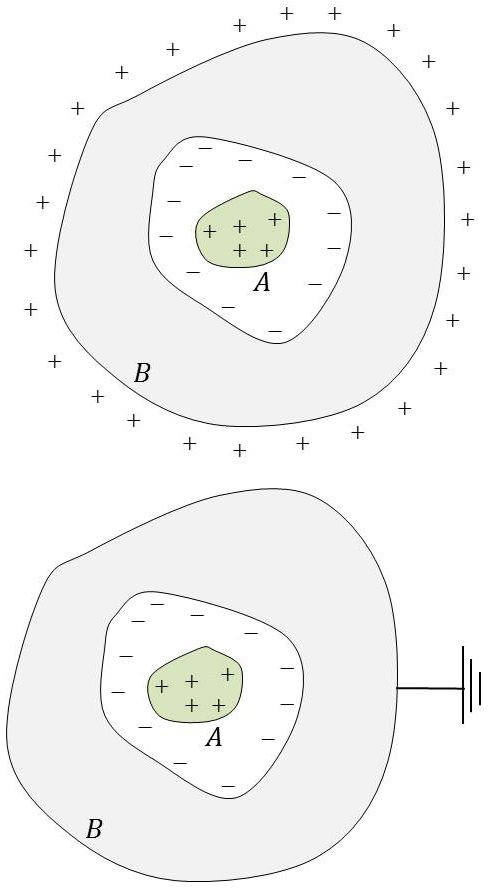 On dit qu’il y a influence totale quand le conducteur influencé entoure complètement le conducteur chargé influençant.
On dit qu’il y a influence totale quand le conducteur influencé entoure complètement le conducteur chargé influençant.
Si le conducteur influencé est isolé, toutes les lignes de force de \(A\) aboutissent sur la surface intérieure de \(B\). D’après le théorème des états correspondants, les charges sur ces deux surfaces sont donc égales et opposées. Si \(B\) est initialement neutre, il apparaît sur sa surface extérieure une charge égale à celle de \(A\).
Si \(B\) est reliée au sol cette charge extérieure, ici positive, est neutralisée par des charges négatives venant du sol.
On peut encore dire qu’il y a influence totale d’un conducteur sur un autre quand toutes les lignes de force parties de l’un aboutissent à l’autre, même si l’un des corps n’entoure pas entièrement l’autre.
3.2. Définitions et propriétés
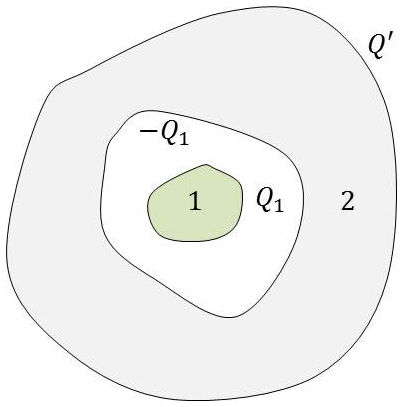
On appelle condensateur un système de deux conducteurs dont l’un entoure complètement l’autre. Il y a donc influence totale.
 La relation : \[Q_i=\sum_{j=1}^{j=k}C_{ij}~V_j\qquad[31]\]
La relation : \[Q_i=\sum_{j=1}^{j=k}C_{ij}~V_j\qquad[31]\]
peut s’écrire : \[\begin{aligned} &Q_1=C_{11}~V_1+C_{12}~V_2\\ &Q_2=C_{21}~V_1+C_{22}~V_2 \end{aligned} \qquad[32]\]
avec : \[C_{12}=C_{21}\quad;\quad C_{11}=-C_{12}\qquad[33]\]
En tenant compte des raisons de symétrie et de l’influence totale, les relations deviennent : \[\begin{aligned} &Q_1=C_{11}(V_1-V_2)\\ &Q_2=-C_{11}V_1+C_{22}V_2=-C_{11}(V_1-V_2)+(C_{22}-C_{11})V_2=-Q_1+Q' \end{aligned} \qquad[34]\]
Comme il y a influence totale, la charge située sur la face interne de \([2]\) est égale à \(-Q\). La charge \(Q'\) est donc la charge qui se trouve sur la face externe de \([2]\).
D’après le théorème des écrans électriques, cette charge se répartit sur la face externe comme si les charges internes n’existaient pas. Donc : \[C'=C_{22}-C_{11}\qquad[35]\]
est la capacité du conducteur \([2]\) isolé dans l’espace.
La grandeur \(C=C_{11}\) s’appelle la capacité du condensateur.
La valeur absolue de la charge \(Q\) de chacune des armatures est la charge du condensateur.
Ces deux grandeurs sont reliées par : \[|Q|=C~~|V_1-V_2|\qquad[36]\]
Si l’un des corps n’entoure pas l’autre, mais si les charges respectives sont égales et opposées, il y a encore influence totale et les formules précédentes sont encore valables.
3.3. Condensateur sphérique
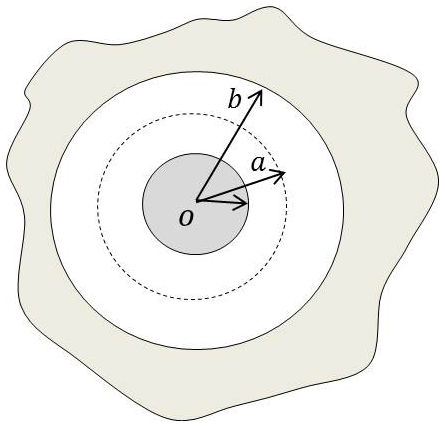 Les armatures sont les faces en regard de deux sphères concentriques.
Les armatures sont les faces en regard de deux sphères concentriques.
Soient \(a\) et \(b\) les rayons respectifs et \(V_1\) et \(V_2\) les potentiels correspondants.
Le potentiel entre les deux armatures est une fonction de Laplace qui se réduit à une constante sur la première armature et à une autre constante sur la deuxième armature.
La solution est unique et on peut prendre : \[V=\frac{A}{r}+B\qquad[37]\]
Pour relier la constante \(A\) à la charge totale \(Q\) de l’armature interne, calculons \(\sigma\) pour \(r=a\) : \[\sigma=-\varepsilon_0~\Big(\frac{\partial V}{\partial r}\Big)_{r=a}=\frac{\varepsilon_0~A}{a^2}\qquad[38]\]
La charge totale de l’armature interne est : \[Q=4\pi~a^2~\sigma=4\pi~\varepsilon_0~A\qquad[39]\]
On peut donc écrire : \[V_a-V_b=A~\Big(\frac{1}{a}-\frac{1}{b}\Big)=\frac{Q}{4\pi~\varepsilon_0}~\frac{b-a}{a~b}\qquad[40]\]
Par suite : \[|Q|=C~~|V_a-V_b|=4\pi~\varepsilon_0~\frac{a~b}{b-a}\qquad[41]\]
Si \(b~\approx~a\) et en posant \(b-a=e\), il vient : \[C~\approx~4\pi~\varepsilon_0~\frac{a^2}{e}=\frac{\varepsilon_0~S}{e}\qquad[42]\]
On retrouve la formule de la capacité du condensateur plan.
Remarque
On aurait obtenu le même résultat et même de manière plus rapide en appliquant le théorème de Gauss.
La surface sphérique intermédiaire (entre les deux armatures) a pour expression : \[S=4\pi~r^2\]
On exprime le fait que la charge intérieure à travers cette surface correspond au flux du champ électrique : \[Q=\varepsilon_0~E~(4\pi~r^2)\quad\Rightarrow\quad E=\frac{Q}{4\pi~\varepsilon_0}~\frac{1}{r^2}\]
D’où l’expression du potentiel par intégration à partir de la relation : \[E=-\frac{\partial V}{\partial r}\quad\Rightarrow\quad V=\frac{A}{r}+B\]
3.4. Condensateur plan
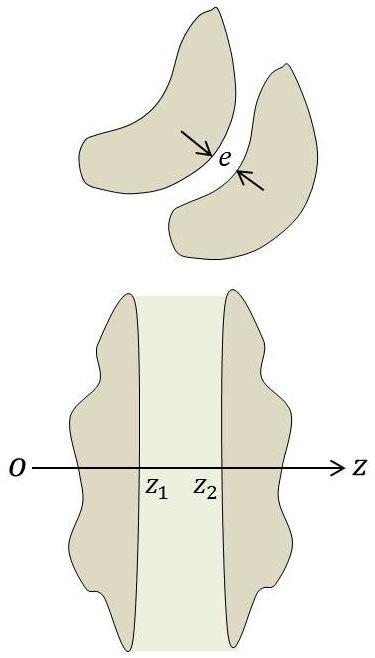 Quand on néglige les perturbations des bords, le potentiel entre les deux armatures est une solution de l’équation de Laplace qui se réduit à une constante sur chacune des armatures.
Quand on néglige les perturbations des bords, le potentiel entre les deux armatures est une solution de l’équation de Laplace qui se réduit à une constante sur chacune des armatures.
On peut prendre : \[V=A~z+B\qquad[43]\]
La densité superficielle sur les armatures est : \[\sigma=-\varepsilon_0~\Big(\frac{\partial V}{\partial z}\Big)_{z=z_1}=-A~\varepsilon_0\qquad[44]\]
Si \(S\) est la surface commune de chaque armature, on a : \[Q=\sigma~S=-\varepsilon_0~A~S\qquad[45]\]
Et on peut écrire : \[V_1-V_2=A~(z_1-z_2)=\frac{e}{\varepsilon_0~S}~Q\qquad[46]\]
D’où la capacité du condensateur plan : \[C=\frac{\varepsilon_0~S}{e}\qquad[47]\]
Quand la distance \(e\) entre les armatures de forme quelconque est constante et très petite, la formule précédente s’applique encore, car le potentiel, sur la normale commune aux surfaces, varie encore linéairement.
3.5. Condensateur cylindrique
 L’équation de Laplace est de la forme : \[V=A~\ln(r)+B\qquad[48]\]
L’équation de Laplace est de la forme : \[V=A~\ln(r)+B\qquad[48]\]
Cette forme est déduite du théorème de Gauss en considérant la charge \(Q\) de l’armature interne et la surface pour le flux \[S=2\pi~r~l\]
On a alors : \[\begin{aligned} Q=\varepsilon_0~E~(2\pi~r~l)\quad&\Rightarrow\quad E=\frac{1}{2\pi~\varepsilon_0~l}~\frac{1}{r}\\ E=-\frac{\partial V}{\partial r}\quad&\Rightarrow\quad V=A~\ln(r)+B \end{aligned} \qquad[49]\]
Pour relier la constante \(A\) à la charge totale de l’armature interne, calculons la densité de charge : \[\sigma=-\varepsilon_0~\Big(\frac{\partial V}{\partial r}\Big)_{r=a}=-\frac{\varepsilon_0~A}{a}\qquad[50]\]
La charge totale de cette armature est donc : \[Q=2\pi~\sigma~a~l=-2\pi~\varepsilon_0~A\qquad[51]\]
Nous pouvons écrire : \[V_b-V_a=A~\ln\frac{b}{a}=\frac{Q}{2\pi~\varepsilon_0~l}~\ln\frac{b}{a}\qquad[52]\]
D’où l’expression de la capacité : \[C=\frac{2\pi~\varepsilon_0~l}{\ln(b/a)}\qquad[53]\]
Cas limite : \[a~\approx~b\quad;\quad a-b=e\quad;\quad \ln~(1-\frac{e}{a})~\approx~\frac{e}{a}\]
On retrouve le cas du condensateur plan : \[C\approx\frac{2\pi~\varepsilon_0~a~l}{e}=\frac{\varepsilon_0~S}{e}\]
Naturellement, ce calcul est approximatif, car les perturbations dues aux bords du cylindre ont été négligées.
3.6. Capacité de deux cylindres parallèles excentrés
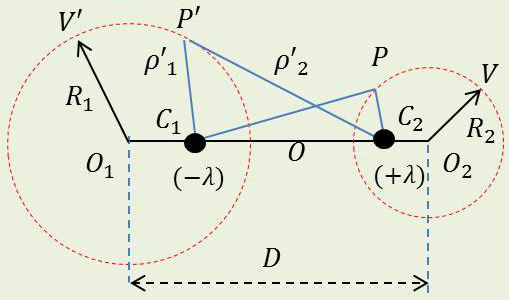 On sait que les potentiels aux points \(P\) et \(P'\) produit par deux lignes parallèles placées aux points \(C_1\) et \(C_2\) portant des densités linéaires \([-\lambda,~+\lambda]\) sont respectivement :
On sait que les potentiels aux points \(P\) et \(P'\) produit par deux lignes parallèles placées aux points \(C_1\) et \(C_2\) portant des densités linéaires \([-\lambda,~+\lambda]\) sont respectivement :
\[\begin{aligned} V&=2~\lambda~\ln\frac{\rho_1}{\rho_2}\\ V'&=2~\lambda~\ln\frac{\rho'_1}{\rho'_2} \end{aligned} \qquad[54]\]
Les équipotentielles (rapports constants) s’appuient sur des circonférences \((O_1,~R_1)\) et \((O_2,~R_2)\).
Tous calculs faits (problème de géométrie), on obtient : \[\begin{aligned} V-V'&=\pm 2~\lambda~\ln(A+\sqrt{A^2-1})=\pm 2~\lambda~\arg~\sinh(A)\\ A&=\frac{D^2-{R_1}^2-{R_2}^2}{2~R_1~R_2} \end{aligned} \qquad[55]\]
Si nous disposons maintenant les deux cylindres de manière qu’ils portent par unité de longueur les charges \(Q=\pm\lambda \), on a : \[|V-V'|=2~|Q|~\arg~\cosh(A)\qquad[56]\]
D’où la capacité : \[C=\frac{1}{2~\arg~\cosh(A)}\qquad[57]\]
Cas particulier
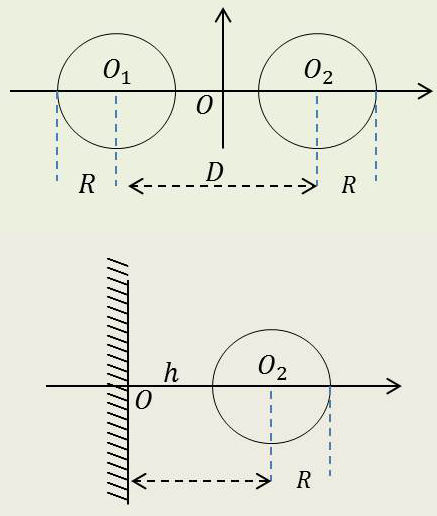 Si deux cylindres sont égaux, ils sont nécessairement extérieurs et on a : \[A=\frac{D^2}{2~R^2}-1=\cosh\frac{1}{2~C}\]
Si deux cylindres sont égaux, ils sont nécessairement extérieurs et on a : \[A=\frac{D^2}{2~R^2}-1=\cosh\frac{1}{2~C}\]
D’où : \[C=\frac{1}{4~\arg~\cosh\cfrac{D}{2~R}}\]
Dans le cas du cylindre et du plan, on considère le plan comme un cylindre de rayon \(R_1\) infini : \[A~\approx~\frac{D^2-R^2}{2~R_1~R_2}=\frac{(D+R_1)~(D-R_1)}{2~R_1~R_2}\]
Tous calculs faits : \[C=\frac{1}{2~\arg~\cosh\cfrac{h}{R}}\]
3.7. Sphères ou cylindres de petites dimensions en présence du sol
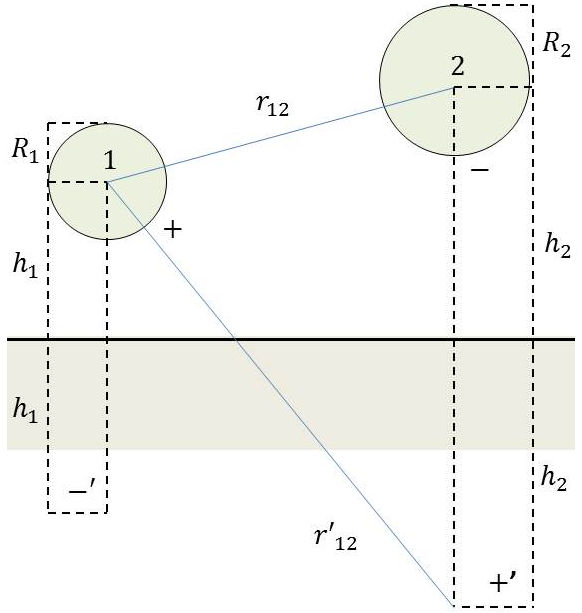 Les dimensions \(R_1\) et \(R_2\) sont très inférieures à \(h_1,~h_2,~r_{12},~r'_{12}\). Les sphères sont assimilables à des points et les cylindres à des lignes uniformément chargées.
Les dimensions \(R_1\) et \(R_2\) sont très inférieures à \(h_1,~h_2,~r_{12},~r'_{12}\). Les sphères sont assimilables à des points et les cylindres à des lignes uniformément chargées.
Pour deux conducteurs ayant des charges opposées, on a aux points [1] et [2] d’après la théorie des images : \[\begin{aligned} &V_1=\frac{Q}{4\pi~\varepsilon}~\Big\{\Big(\frac{1}{R_1}-\frac{1}{2~h_1}\Big)-\Big(\frac{1}{r_{12}}-\frac{1}{r'_{12}}\Big)\Big\}\\ &V_1=\frac{Q}{4\pi~\varepsilon}~\Big\{\Big(\frac{1}{r_{12}}-\frac{1}{r'_{12}}\Big)-\Big(\frac{1}{R_2}-\frac{1}{2~h_2}\Big)\Big\} \end{aligned} \qquad[58]\]
En calculant la différence \((V_1-V_2)\), on en déduit la capacité du système : \[\frac{1}{C}=\frac{1}{4\pi~\varepsilon}~\Big\{\Big(\frac{1}{R_1}+\frac{1}{R_2}-\frac{2}{r_{12}}\Big)-\Big(\frac{1}{2~h_1}+\frac{1}{2~h_2}-\frac{2}{r'_{12}}\Big)\Big\}\qquad[59]\]

