1. Courant électrique

Nous n’étudierons que les champs indépendant du temps comme ceux produits par les courants permanents circulant dans les conducteurs. On considère qu’ils sont dus à des charges électriques en mouvement.

Si \(\rho(x,~y,~z)\) désigne la densité volumique de ces charges et \(\overrightarrow{v}(x,~y,~z)\) le champ des vitesses, on définit un vecteur densité de courant \(\overrightarrow{i}\) : \[\overrightarrow{i}=\rho~\overrightarrow{v}\qquad[1]\]

\(\overrightarrow{v}\) est la vitesse moyenne du déplacement d’ensemble et ordonné de ces charges.

En fait, notamment dans les métaux, une agitation désordonnée du gaz électronique subsiste toujours, mais elle ne se traduit par rien d’observable en ce qui concerne le champ magnétostatique, l’objet de notre étude.

Cette vitesse moyenne d’ensemble \(\overrightarrow{v}\) est très petite, de l’ordre du centimètre par seconde, alors que les vitesses d’agitation, sensiblement indépendantes de la température, se chiffrent en milliers de kilomètres par seconde.

Comme nous ne considérons que des phénomènes permanents, \(\rho\) est indépendant du temps. Il s’en suit que la quantité d’électricité localisée dans un élément de volume déterminé est toujours la même.

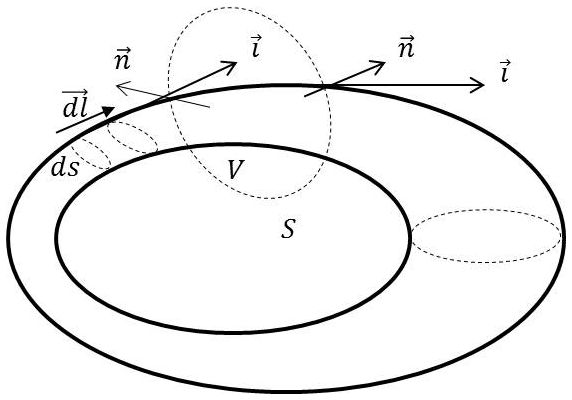Imaginons une surface fermée \(S\) limitant un volume \(v\) dans le conducteur.

La quantité d’électricité qui sort de ce volume doit être égale à celle qui y entre. La quantité d’électricité traversant l’élément \(dS\) de surface en une seconde étant : \[\rho~\overrightarrow{v}\cdot\overrightarrow{n}~dS\]

On a donc : \[\int_S\rho~(\overrightarrow{v}\cdot\overrightarrow{n})~dS=\int_S(\overrightarrow{i}\cdot\overrightarrow{n})~dS=\int_v \rm div(\overrightarrow{i})~dv=0\qquad[2]\]

\(v\) étant quelconque, on doit avoir en tout point du volume du conducteur : \[\rm div(\overrightarrow{i})=0\qquad[3]\]

Les conducteurs sont généralement limités par une surface \(\Sigma\).

Les charges, à priori intérieures au conducteur, ne traversent pas cette surface et on doit avoir en chacun de ses points : \[\big(\overrightarrow{n}\cdot\overrightarrow{i}\big)_{\Sigma}=0\qquad[4]\]

On appelle ligne de courant une ligne tangente au vecteur en chacun de ses points.

Toutes les lignes de courant qui s’appuient sur le pourtour d’un élément de surface \(dS\) forment une sorte de tube appelé tube de courant élémentaire.

Le vecteur ayant une divergence nulle, les tubes de courant ne peuvent que se fermer sur eux-mêmes, fait inhérent à l’hypothèse de permanence. Les charges circulent donc dans les tubes de courant à la manière d’un fluide incompressible dans un tuyau fermé.

La quantité d’électricité qui traverse par seconde la section normale du tube est la même en tout point du tube : c’est l’intensité du courant dans le tube élémentaire : \[dI=(\overrightarrow{n}\cdot\overrightarrow{i})~dS=i~dS_n\qquad[5]\]

Si \(\overrightarrow{dl}\) est l’élément d’arc de la ligne de courant, on a : \[dI~\overrightarrow{dl}=\overrightarrow{i}~dv\qquad[6]\]

\(dv\) : élément de volume du tube.

Considérons l’intensité totale à travers une surface \(S\). Par définition, c’est la quantité totale d’électricité qui passe à travers \(S\) pendant une seconde : \[J=\int_S(\overrightarrow{n}\cdot\overrightarrow{i})~dS\qquad[7]\]

Nous commencerons par étudier les courants qui circulent dans des fils : ce sont les courants linéaires. Ces circuits ne sont pas rigoureusement filiformes, mais il suffit que les dimensions transversales soient très petites par rapport à la longueur pour que ces conditions soient applicables.

Relation de l’intensité \(I\) du courant qui les traverse à la densité de courant et à la section : \[I=i~S\qquad[8]\]

S’y ajoute la relation à la quantité de courant : \(dQ=I~dt\).

2. Loi des actions électrodynamiques d’Ampère

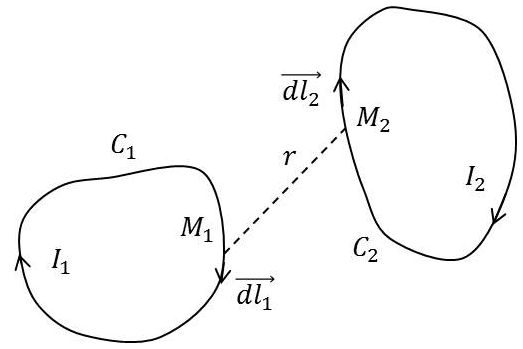Nous admettrons, comme un fait d’expérience, la formule exprimant la force \(\overrightarrow{F_2}\) que le courant \(C_1\) d’intensité \(I_1\) exerce sur le courant \(C_2\) d’intensité \(I_2\) : \[\overrightarrow{F_2}=\frac{\mu_0}{4\pi}~I_1~I_2\int_{C1}\int_{C2}\Big\{\overrightarrow{dl_2}\wedge\Big(\overrightarrow{dl_1}\wedge\frac{\overrightarrow{r}}{r^3}\Big)\Big\}\qquad[9]\]

On peut aisément vérifier que les forces sont opposées : \[\overrightarrow{F_1}=-\overrightarrow{F_2}\]

On écrira plus simplement : \[\overrightarrow{F_2}=\frac{\mu_0}{4\pi}~I_1~I_2\int_{C1}\int_{C2} (\overrightarrow{dl_1}\cdot\overrightarrow{dl_2})~\frac{\overrightarrow{r}}{r^3}\qquad[10]\]

Si l’on avait des charges réparties sur ces mêmes circuits avec des densités linéaires uniformes (\(\lambda_1,~\lambda_2\)), nous aurions, d’après la loi de Coulomb : \[\overrightarrow{F_2}=-\overrightarrow{F_1}=\frac{\mu_0}{4\pi}~\lambda_1~\lambda_2\int_{C1}\int_{C2} (\overrightarrow{dl_1}\cdot\overrightarrow{dl_2})~\frac{\overrightarrow{r}}{r^3}\qquad[11]\]

Formules qui permettent de définir l’unité de courant, l’ampère (A) :

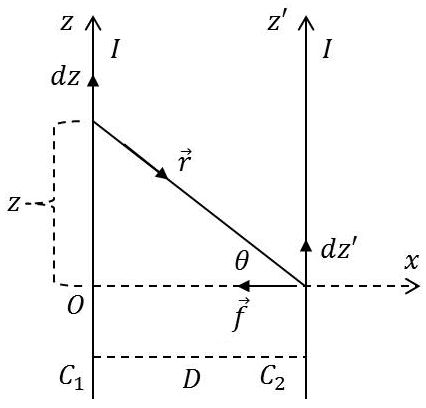Calculons la force qui s’exerce entre deux courants parallèles indéfinis de même sens et de même intensité. La composante de la force suivant \(Ox\) est donnée par : \[\begin{aligned} &F_x=-\frac{\mu_0}{4\pi}~I^2\int_{C1} dz'\int_{C2}\frac{D}{r^3}~dz\\ &F_x=-\frac{2~I^2}{D}~\frac{\mu_0}{4\pi}\int_{C1} dz'\int_0^{\pi/2}\cos\theta~d\theta\\ &F_x=-\frac{2~I^2}{D}~\frac{\mu_0}{4\pi}\int_{-\infty}^{+\infty} dz' \end{aligned} \qquad[12]\]

La force totale est infinie, mais on peut parler de la force que \(C_1\) exerce sur une longueur donnée de \(C_2\). Cette force suivant l’axe des \(x\), accessible à l’expérience a pour expression : \[F_x=-\frac{\mu_0}{4\pi}~2~I^2~\frac{l}{D}\qquad[13]\]

Les autres composantes de la force étant nulles.

En posant par convention : \[\mu_0=4\pi\times 10^{-7}\qquad[14]\]

on tire la définition suivante de l’intensité de courant :

L’unité d’intensité de courant, l’ampère, est l’intensité d’un courant constant qui, maintenue dans deux conducteurs parallèles, rectilignes, de longueur infinie, de section circulaire négligeable et placés à un mètre l’un de l’autre dans le vide, produirait entre ces deux conducteurs une force égale à \(2\times 10^{-7}~\)newtons par mètre de longueur.

2.1. Induction magnétique. Loi de Biot et Savart. Force de Laplace

Les formules précédentes ont l’avantage de se prêter à une vérification expérimentale directe, mais elles restent toutefois simplistes. On obtient des formules d’une portée bien plus générale et qui correspondent mieux à la réalité physique en admettant que chacun des courants crée une induction magnétique, cette dernière agissant sur l’autre courant.

Nous poserons donc : \[\begin{aligned} \overrightarrow{B_1}&=\frac{\mu_0~I_1}{4\pi}\int_{C1}\overrightarrow{dl_1}\wedge\frac{\overrightarrow{r}}{r^3}\\ \overrightarrow{F_2}&=I_2\int_{C2}\overrightarrow{dl_2}\wedge\overrightarrow{B_1} \end{aligned} \qquad[15]\]

Si plusieurs courants sont en présence, les forces exercées respectivement par tous les autres courants sur l’un d’entre eux, le \(i^{\text{ème}}\) par exemple, s’ajoutent géométriquement : \[\overrightarrow{F_i}=\sum_j\overrightarrow{F_{i,j}}\qquad[16]\]

\(\overrightarrow{F_{i,j}}\) : force exercée par le \(j^{\text{ème}}\) courant sur le \(i^{\text{ème}}\).

Il en sera ainsi avec l’expression de la force si l’on a : \[\overrightarrow{B_i}=\sum_j^{j\neq i}\overrightarrow{B_{i,j}}\qquad[17]\]

c’est-à-dire si les inductions s’ajoutent aussi géométriquement. Cette propriété de superposition des inductions est très importante : elle se traduira plus loin par des équations aux dérivées partielles linéaires.

2.2. Potentiel vecteur d’un courant linéaire

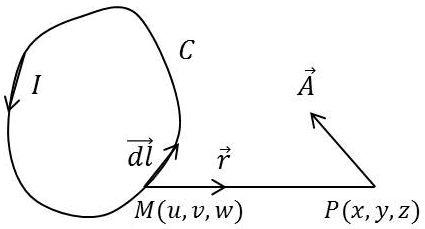La forme de produit vectoriel du vecteur induction montre que l’on peut écrire : \[\overrightarrow{B}=\overrightarrow{\rm rot}\overrightarrow{A}\quad;\quad\overrightarrow{A}=\frac{\mu_0~I}{4\pi}\int_C\frac{\overrightarrow{dl}}{r}\qquad[18]\]

Un calcul analytique élémentaire (dérivées prises par rapport aux coordonnées x, y, z) permettrait de le vérifier.

\(\overrightarrow{A}\) est appelé potentiel vecteur du courant. L’induction \(\overrightarrow{B}\) dérive de \(\overrightarrow{A}\) par la formule du rotationnel.

Remarques

– Si on admet que seule l’induction \(\overrightarrow{B}\) a un sens physique et qu’elle est bien déterminée, on voit que le potentiel vecteur \(\overrightarrow{A}\) n’est défini qu’à un gradient près, car le rotationnel d’un gradient est toujours nul.

– S’il y a \(k\) circuits, nous avons vu que leurs inductions s’ajoutaient au point \(P\). Il en est donc de même pour leurs potentiels vecteurs : \[\overrightarrow{A}=\frac{\mu_0}{4\pi}~\sum_{j=1}^{j=k}I_j\int_{Cj}\frac{dl_j}{r}\qquad[19]\]

2.3. Distribution continue de courant occupant un volume limité

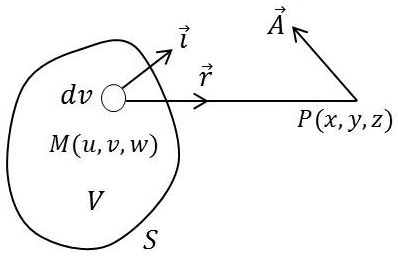Dans le cas d’une distribution continue de courants à l’intérieur d’un volume \(v\) limité par une surface \(S\), la somme précédente (19) devient une intégrale : \[\overrightarrow{A}=\frac{\mu_0}{4\pi}\int dI\int_C\frac{\overrightarrow{dl}}{r}\qquad[20]\]

La première intégrale est prise le long d’une ligne de courant et \(dI\) est l’intensité du courant dans le tube élémentaire correspondant. La somme pour tous les tubes de courant donne une intégrale étendue à tout le volume \(v\).

En se référant à la relation première : \[dI~\overrightarrow{dl}=\overrightarrow{i}~dv\]

cette intégrale devient : \[\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_v\frac{\overrightarrow{i}}{r}dv\qquad[21]\]

Pour chacune des composantes de \(\overrightarrow{A}\), on a une intégrale qui est du même type que l’intégrale du potentiel coulombien.

Pour l’induction : \[\begin{aligned} &\overrightarrow{B}=\overrightarrow{\rm rot}\overrightarrow{A}=-\frac{\mu_0}{4\pi}\int_v\Big\{\overrightarrow{i}\wedge\overrightarrow{\rm grad}\Big(\frac{1}{r}\Big)\Big\}~dv\\ &\overrightarrow{B}=\overrightarrow{\rm rot}\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_v\Big\{\overrightarrow{i}\wedge\Big(\frac{\overrightarrow{r}}{r^3}\Big)\Big\}~dv \end{aligned} \qquad[22]\]

2.4. Équations aux dérivées partielles du potentiel vecteur

On part de l’expression intégrale de \(\overrightarrow{A}\) : \[\overrightarrow{A}=\frac{\mu_0}{4\pi}\int_v\frac{\overrightarrow{i}}{r}~dv\]

Compte tenu des propriétés du Laplacien de (\(1/r\)), on a : \[\Delta\overrightarrow{A}=-\mu_0~\overrightarrow{i}\qquad[23]\]

Prenant la divergence des deux membres de (23) et sachant par ailleurs que : \[(\overrightarrow{n}\cdot\overrightarrow{i})_S=0\quad;\quad \rm div(\overrightarrow{i})=0\qquad[24]\]

il vient pour le potentiel vecteur : \[\rm div(\overrightarrow{A})=0\qquad[25]\]

2.5. Équations fondamentales du champ magnétostatique

Tout d’abord, les résultats classiques à partir de l’analyse vectorielle : \[\begin{aligned} \overrightarrow{B}&=\overrightarrow{\rm rot}\overrightarrow{A}\quad\Rightarrow\quad\rm div(\overrightarrow{B})=0\\ \overrightarrow{\rm rot}\overrightarrow{A}&=\overrightarrow{\rm grad}(\rm div(\overrightarrow{A}))-\Delta\overrightarrow{A}\\ \overrightarrow{\rm rot}\overrightarrow{B}&=\mu_0~\overrightarrow{i} \end{aligned} \qquad[26]\]

Pour faire disparaître \(\mu_0\) et pour avoir des équations inchangées en présence des diélectriques, nous introduisons à côté du vecteur induction \(\overrightarrow{B}\) un autre vecteur, le champ magnétique \(\overrightarrow{H}\) défini ici par : \[\overrightarrow{B}=\mu_0~\overrightarrow{H}\quad\Rightarrow\quad\overrightarrow{\rm rot}\overrightarrow{H}=\overrightarrow{i}\qquad[27]\]

Les deux équations : \[\rm div(\overrightarrow{B})=0\quad;\quad\overrightarrow{\rm rot}\overrightarrow{H}=\overrightarrow{i}\qquad[28]\]

sont les équations fondamentales du champ magnétostatique.

Ce champ est ainsi défini par les deux vecteurs (\(\overrightarrow{B},~\overrightarrow{H}\)) liés dans le vide par la relation : \[\overrightarrow{B}=\mu_0~\overrightarrow{H}\qquad[29]\]

Ces équations sont du premier ordre et linéaires ; elles satisfont donc au principe de superposition, c’est-à-dire que si l’on a deux solutions, leur somme est encore une solution.

Pour obtenir des équations du second ordre, il suffit de faire : \[\overrightarrow{\rm rot}\overrightarrow{\rm rot}\overrightarrow{H}=\overrightarrow{\rm rot}\overrightarrow{i}\]

et d’utiliser une fois de plus l’identité[29,2].

Il vient : \[\Delta\overrightarrow{H}=\overrightarrow{\rm rot}\overrightarrow{i}\quad\text{ou}\quad\Delta\overrightarrow{B}=-\mu_0~\overrightarrow{\rm rot}\overrightarrow{i}\qquad[30]\]

En particulier dans le vide (\(\overrightarrow{i}=\overrightarrow{0}\)) : \[\Delta\overrightarrow{H}=0\quad\text{ou}\quad\Delta\overrightarrow{B}=0\qquad[31]\]

Remarque

Une difficulté se présente avec ces équations, car la densité \(\overrightarrow{i}\) est en général discontinue à la surface des conducteurs où elle passe brusquement d’une valeur finie à une valeur infinie.

Pour des raisons de simplicité, on dira par exemple que cette densité est constante à l’intérieur d’un cylindre indéfini et que cette densité est nulle à l’extérieur. En réalité, il doit y avoir une brusque diminution au voisinage immédiat de la surface et non une discontinuité.

2.6. Forme intégrale des équations du champ

2.6.1. Conservation du flux d’induction

Intégrons l’équation : \[\rm div(\overrightarrow{B}=0)\]

dans un volume \(v\) limité par une surface \(S\) et transformons en intégrale de surface: \[\int_v {\rm div}(\overrightarrow{B})~dv=\int_S(\overrightarrow{n}\cdot\overrightarrow{B})~dS\qquad[31]\]

La deuxième intégrale représente le flux du vecteur \(\overrightarrow{B}\) à travers la surface \(S\) et on voit que ce flux est nul.

On dit que le flux du vecteur \(\overrightarrow{B}\) ou flux d’induction est conservatif.

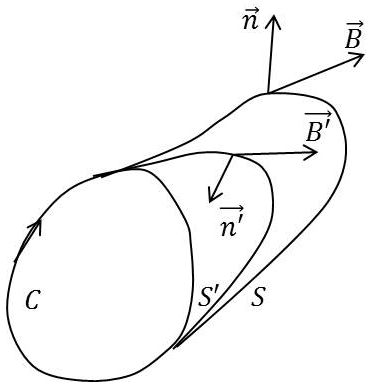Considérons un courant linéaire fermé \(C\) ou un tube de courant élémentaire. Le flux \(\Phi\) du vecteur induction produit par le courant lui-même ou par d’autres courants situés à son voisinage est défini par : \[\Phi=\int_S(\overrightarrow{n}\cdot\overrightarrow{B})~dS\qquad[32]\]

S est une surface quelconque s’appuyant sur le contour \(C\).

On peut voir que ce flux est indépendant de la surface \(S\). Si l’on prend en effet une autre surface \(S'\) s’appuyant sur le même contour on a : \[\int_{S+S'}(\overrightarrow{n}\cdot\overrightarrow{B})~dS=0\qquad[33]\]

car \(S+S'\) est une surface fermée.

Par ailleurs : \[\overrightarrow{n'}=-\overrightarrow{n}\qquad\text{donc :}\quad\Phi'=\Phi\qquad[34]\]

En remplaçant \(\overrightarrow{B}\) par son expression en fonction du potentiel vecteur, on peut écrire : \[\Phi=\int_S(\overrightarrow{n}\cdot\overrightarrow{\rm rot}\overrightarrow{A})~dS=\int_C\overrightarrow{A}\cdot\overrightarrow{dl}\qquad[35]\]

Le flux est donc égal à la circulation du potentiel vecteur le long de la courbe \(C\).

2.6.2. Théorème d’Ampère

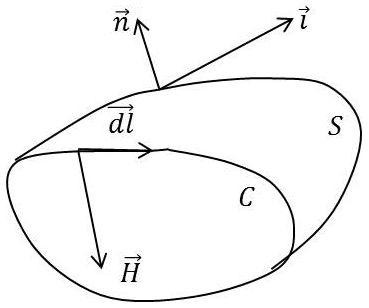Pour transformer la deuxième équation : \[\overrightarrow{\rm rot}\overrightarrow{H}=\overrightarrow{i}\qquad[36]\]

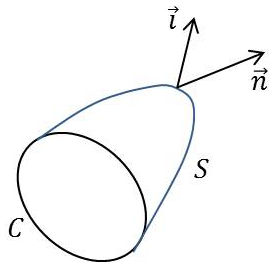
nous considérons une surface fictive \(S\) qui s’appuie sur une courbe fermée \(C\) dans une région où circulent des courants avec une densité \(\overrightarrow{i}\).

Le sens de circulation sur la courbe \(C\) par rapport à la normale \(\overrightarrow{n}\) à la surface \(S\) est le même que le sens de rotation autour de \(Ox_3\) qui amène \(Ox_1\) sur \(Ox_2\) dans un trièdre direct.

Multiplions scalairement les deux membres de la formule par \(\overrightarrow{n}\) et intégrons sur \(S\) : \[\int_S(\overrightarrow{n}\cdot\overrightarrow{\rm rot}\overrightarrow{H})~dS=\int_S(\overrightarrow{i}\cdot\overrightarrow{n})~dS\qquad[37]\]

La première intégrale se transforme en intégrale curviligne et la deuxième représente l’intensité totale \(J\) du courant à travers la surface \(S\). Il reste donc : \[\int_C\overrightarrow{H}\cdot\overrightarrow{dl}=J\qquad[38]\]

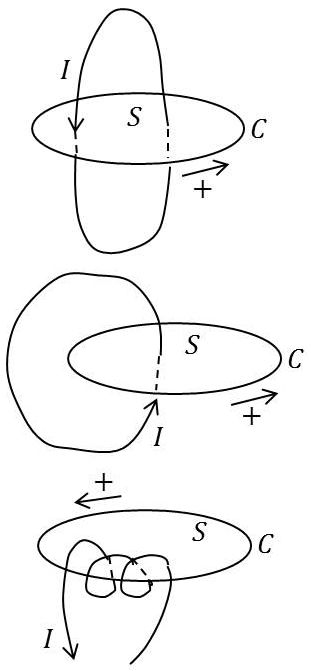C’est l’expression du théorème d’Ampère :

La circulation du vecteur champ magnétique le long d’une courbe fermée \(C\) limitant une surface \(S\) est égale à l’intensité totale du courant à travers cette surface.

En particulier pour un courant linéaire d’intensité \(I\) coupant une surface \(S\) et s’appuyant sur le contour \(C\).

• figure 1 : \(J=I\)

• figure 2 : \(J=0\)

• figure 3 où un même courant d’intensité \(I\) coupe \(n\) fois la surface \(S\), on a \(J=n~I\) et : \[\int_C\overrightarrow{H}\cdot\overrightarrow{dl}=n~I\qquad[39]\]

formule qui montre que le champ magnétique d’un courant peut s’exprimer en ampères tours par mètre.