1. Relation générale entre les tensions et les déformations

Il s’agit toujours de tensions et de déformations locales. Nous nous plaçons tout d’abord dans le cas général d’un solide anisotrope (cristal quelconque orienté de façon arbitraire par rapport aux axes \(Ox_1,~Ox_2,~Ox_3\)).

Un système local d’efforts représenté par le tenseur \(t_{ij}\) va entraîner un système de déformations représenté par le tenseur \(d_{kl}\). Nous supposons que l’état initial, avant déformation, est un état de repos où le solide n’est soumis à aucun effort extérieur.

Les déformations étant petites, à partir de l’équilibre, les efforts vont être représentables, au second ordre près, par des fonctions linéaires et homogènes des déformations. Nous écrirons donc, en représentant les glissements par les quantités (\(2~g_i\)), nous verrons plus loin pourquoi :

\[\begin{aligned} N_1=n_1^1~a_1+n_1^2a_2+n_1^3~a_3+\nu_1^1~(2~g_1)+\nu_1^2~(2~g_2)+\nu_1^3~(2~g_3)\\ N_2=n_2^1~a_1+n_2^2a_2+n_2^3~a_3+\nu_2^1~(2~g_1)+\nu_2^2~(2~g_2)+\nu_2^3~(2~g_3)\\ N_3=n_3^1~a_1+n_3^2a_2+n_3^3~a_3+\nu_3^1~(2~g_1)+\nu_3^2~(2~g_2)+\nu_3^3~(2~g_3)\\ \\ T_1=\tau_1^1~a_1+\tau_1^2~a_2+\tau_1^3a_3+\theta_1^1~(2~g_1)+\theta_1^2~(2~g_2)+\theta_1^3~(2~g_3)\\ T_2=\tau_2^1~a_1+\tau_2^2~a_2+\tau_2^3a_3+\theta_2^1~(2~g_1)+\theta_2^2~(2~g_2)+\theta_2^3~(2~g_3)\\ T_3=\tau_3^1~a_1+\tau_3^2~a_2+\tau_3^3a_3+\theta_3^1~(2~g_1)+\theta_3^2~(2~g_2)+\theta_3^3~(2~g_3)\end{aligned}\]

Nous introduisons ainsi 6 x 6 = 36 coefficients, mais 30 d’entre eux sont égaux deux à deux. En effet, cherchons l’expression du travail effectué par les efforts \(t_{ij}\) lors d’une modification infinitésimale des déformations \(a_i\) et \(g_i\).

Isolons par la pensée dans le solide, autour du point considéré, un petit élément de volume en forme (avant la déformation) de petit parallélépipède d’arêtes (\(l_1,~l_2,~l_3\)) parallèles aux axes de coordonnées.

Une modification \(da_1\) de l’allongement \(a_1\) nécessaire de la part de l’effort normal \(N_1~l_2~l_3\) un travail : \[dW_1=N_1~l_2~l_3~dl_1=V~N_1~da_1\qquad\text{avec :}\quad V=l_1~l_2~l_3\]

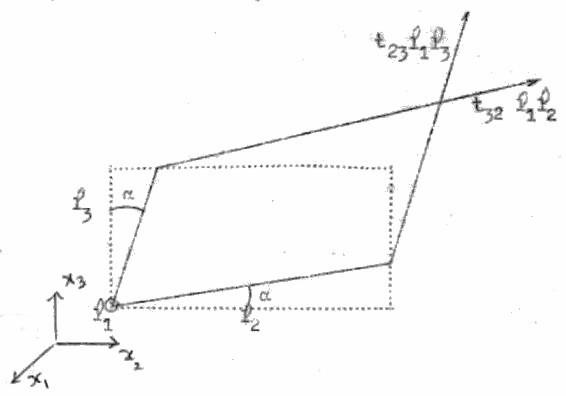Une modification \(dg_1\) du glissement \(g_1\) nécessite de la part des efforts \(t_{23}~l_1~l_2\) et \(t_{32}~l_1~l_2\) des travaux (figure ci-contre) \(t_{23}~l_1~l_2~l_3~d\alpha\) et \(t_{32}~l_1~l_2~l_3d\alpha'\), avec \(t_{23}=t_{32}=T_1\) et \(\alpha+\alpha'=2~g_1\).

Soit un travail total pour la modification \(dg_1\) : \[dW'_1=V~T_1~d(2~g_1)\]

Le travail total nécessité par l’ensemble des modifications (\(da_i,~da_j\)) s’écrit donc : \[dW=V~\Big(\sum N_i~da_i+\sum T_i~d(2~g_i)\Big)\]

La transformation étant réversible et isotherme (ou adiabatique), \(dW\) est la différentielle d’une fonction énergie potentielle et nous pouvons écrire des relations du type :

\[\begin{aligned} \frac{\partial N_i}{\partial a_j}&=\frac{\partial N_j}{\partial a_i}\\ \frac{\partial N_i}{\partial(2~g_j)}&=\frac{\partial T_j}{\partial a_i}\\ \frac{\partial T_i}{\partial(2~g_j)}&=\frac{\partial T_j}{\partial(2~g_i)}\end{aligned}\]

Ce qui revient à dire que le tableau des coefficients {\(n_1^1,~\dots,~g_3^3\)} est symétrique par rapport à la diagonale qui contient les termes \(n_i^i\) et \(\theta_i^i\). Il y a donc 6 coefficients diagonaux et 30 coefficients non diagonaux deux à deux égaux, soit au total : 6 + 30/2 = 21 coefficients indépendants, ceci dans le cas général d’un cristal oblique. Pour un cristal présentant quelques symétries, le nombre de coefficients indépendants diminue.

Supposons par exemple que le cristal présente trois plans de symétrie deux à deux orthogonaux ; nous orientons parallèlement à ces trois plans nos plans de coordonnées. Nous devrons considérer que le milieu solide constitué par notre parallélépipède rectangle est symétrique dans toutes ses propriétés par rapport aux trois plans (\(x_1x_2,~x_2x_3,~x_1x_3\)) passant par son centre (tout au moins avant déformation).

Appliquons alors au parallélépipède des déformations qui se réduisent à des dilatations sans glissement ; les déformations admettent les trois plans considérés comme plans de symétrie, le milieu également. Il en est donc de même des efforts qui ne peuvent donc être que des efforts normaux puisque le glissement \(g_1\) par exemple n’admet comme plan de symétrie que le plan \(x_2x_3\).

Il en résulte immédiatement que tous les coefficients \(\tau_i^j\) sont nuls et il en est de même pour les coefficients \(\nu_i^j\) (par symétrie autour de la diagonale du tableau des coefficients).

Appliquons au parallélépipède la seule déformation \(g_1\) ; les seuls efforts qui peuvent apparaître présentent la symétrie par rapport au plan \(x_2x_3\)  ; il ne peut donc s’agir que des efforts normaux (exclus puisque les \(\nu_i^j\) sont nuls) et que l’effort \(T_1\) admet cette symétrie.

On a donc \(\theta_2^1=\theta_3^1=0\) et, de la même façon, tous les \(\theta_i^j\) à deux indices différents s’annulent ; le tableau ne comporte plus que 9 coefficients distincts différents de zéro.

Passons à un cristal admettant la symétrie du cube (orienté parallèlement aux axes). Les coefficients doivent rester inchangés par permutation circulaire des axes ; il en résulte :

\[\begin{aligned} n_1^1&=n_2^2=n_3^3\\ \theta_1^1&=\theta_2^2=\theta_3^3\\ n_1^2&=n_2^3=n_3^1=n_1^3=n_2^1=n_3^2\end{aligned}\]

Il ne reste plus que trois coefficients distincts.

1.1. Cas du milieu isotrope

Le milieu isotrope admet, par rapport à un système d’axes trirectangles quelconque, toutes les symétries que le cristal cubique admet par rapport à ses arêtes.

Nous pourrons donc écrire, quel que soit le système d’axes trirectangles choisi, la relation entre les tensions et les efforts sous la forme : \[\begin{aligned} &N_1=A~a_1+B~(a_2+a_3)\\ &N_2=A~a_2+B~(a_3+a_1)\\ &N_3=A~a_3+B~(a_1+a_2) \end{aligned} \quad\text{ou}\quad \begin{aligned} &N_1=(A-B)~a_1+B~\theta\\ &N_2=(A-B)~a_2+B~\theta\\ &N_3=(A-B)~a_3+B~\theta \end{aligned} \quad\text{et}\quad \begin{aligned} &T_1=C~(2~g_1)\\ &T_2=C~(2~g_2)\\ &T_3=C~(2~g_3) \end{aligned}\]

Par ailleurs, le milieu étant isotrope, les coefficients A, B et C restent invariants lors d’une rotation quelconque des axes.

Nous sommes, dès lors, parfaitement libres de choisir, pour représenter les déformations locales, le système d’axes principaux du tenseur des déformations ; dans ce nouveau système d’axes, les glissements s’annulent et, par suite, également les efforts tranchants \(T_i\).

Dans le milieu isotrope, les deux tenseurs ont par suite mêmes axes principaux en tout points (bien entendu, l’orientation des axes principaux varie d’un point à l’autre du solide soumis à un système d’efforts quelconque).

Envisageons maintenant un système d’efforts qui conduit à une dilatation nulle, c’est-à-dire que l’on a : \(a_1+a_2+a_3=0\). Dans le système d’axes principaux commun aux deux tenseurs, les composantes s’écrivent :

\[\begin{aligned} t'_{ij}&= \begin{pmatrix} (A-B)~a'_1&0&0\\ 0&(A-B)~a'_1&0\\ 0&0&(A-B)~a'_1 \end{pmatrix}\\ \text{et}\quad d'{ij}&= \begin{pmatrix} a'_1&0&0\\ 0&a'_2&0\\ 0&0&a'_3 \end{pmatrix}\end{aligned}\]

Les deux tenseurs ont dès lors leurs composantes proportionnelles dans leur système d’axes principaux. Ils ont aussi des composantes proportionnelles dans un système trirectangle quelconque obtenu par rotation du système d’axes initialement choisi. On en déduit immédiatement que : \[\frac{T_i}{g_i}=A-B\qquad\text{soit :}\quad C=\frac{A-B}{2}\]

Posons : \[B=\lambda\qquad;\qquad C=\frac{A-B}{2}=\mu\]

Nous obtenons les relations générales entre les tensions et les efforts dans un matériau isotrope :

\[\begin{aligned} N_1&=\lambda~\theta+2~\mu~a_1\\ N_2&=\lambda~\theta+2~\mu~a_2\\ N_3&=\lambda~\theta+2~\mu~a_3\end{aligned}\]

\(\lambda\) et \(\mu\) sont donc les deux coefficients de Lamé.

\[\begin{aligned} T_1&=2~\mu~g_1\\ T_2&=2~\mu~g_2\\ T_3&=2~\mu~g_3\end{aligned}\]

Un matériau réel est la plupart du temps cristallisé, donc localement anisotrope. On pourra cependant considérer qu’un métal par exemple, formé d’un grand nombre de cristaux juxtaposés de très petites dimensions, se comporte comme un matériau isotrope lorsque les efforts sont uniformes dans un domaine assez étendu pour contenir un très grand nombre de cristaux.

2. Propagation des vibrations dans un milieu solide isotrope

Nous supposons que le milieu solide n’est soumis à aucun effort extérieur et négligeons donc en particulier les forces de gravitation. La résultante des efforts de tension appliqués à un parallélépipède élémentaire sert donc uniquement à équilibrer la force d’inertie de ce parallélépipède.

Nous obtiendrons donc l’équation de propagation des vibrations en remplaçant, dans les équations qui expriment l’équilibre du parallélépipède élémentaire, la force \(\overrightarrow{X}~dv\) par la force d’inertie, soit : \[\overrightarrow{X}~dv=-\rho~dv~\overrightarrow{\gamma}=-\rho~dv~\frac{\partial^2\overrightarrow{u}}{\partial t^2}\]

La première condition d’équilibre (composantes des forces suivant \(Ox_1\)) s’écrit dès lors : \[\rho~\frac{\partial^2\overrightarrow{u_1}}{\partial t^2}=\frac{\partial t_{11}}{\partial x_1}+\frac{\partial t_{21}}{\partial x_2}+\frac{\partial t_{31}}{\partial x_3}\]

Avec :

\[\begin{aligned} &t_{11}=N_1=\lambda~\theta+2~\mu~\frac{\partial u_1}{\partial x_1}\\ &t_{31}=T_2=2~\mu~g_2=\mu~\Big(\frac{\partial u_1}{\partial x_3}+\frac{\partial u_3}{\partial x_1}\Big)\\ &t_{21}=T_3=2~\mu~g_3=\mu~\Big(\frac{\partial u_1}{\partial x_2}+\frac{\partial u_2}{\partial x_1}\Big)\end{aligned}\]

Il vient donc : \[\rho~\frac{\partial^2u_1}{\partial t^2} =\lambda~\frac{\partial\theta}{\partial x_1}+2~\mu~\frac{\partial^2u_1}{\partial x_1^2} +\mu~\Big(\frac{\partial^2u_1}{\partial x_3^2}+\frac{\partial^2u_3}{\partial x_1~\partial x_3}+\frac{\partial^2u_1}{\partial x_2^2}+\frac{\partial^2u_2}{\partial x_2~\partial x_1}\Big)\]

Ce qui peut s’écrire : \[\rho~\frac{\partial^2u_1}{\partial t^2}=(\lambda+\mu)~\frac{\partial\theta}{\partial x_1}+\mu~\Delta u_1 \qquad\text{car :}\quad \frac{\partial u_1}{\partial x_1}+\frac{\partial u_2}{\partial x_2}+\frac{\partial u_3}{\partial x_3}=0\]

L’ensemble de l’équilibre dans les trois directions s’exprime donc sous la forme vectorielle : \[\rho~\frac{\partial^2\overrightarrow{u}}{\partial t^2}=(\lambda+\mu)~\overrightarrow{\rm grad}(\theta)+\mu~\Delta\overrightarrow{u}\]

Prenant la divergence de cette expression, nous obtenons, en remarquant que \(\theta=\rm div(\overrightarrow{u})\) et que \(\rm div[\overrightarrow{\rm grad}(\theta)]=\Delta\theta\), on peut écrire : \[\rho~\frac{\partial^2\theta}{\partial t^2}=(\lambda+2~\mu)~\Delta\theta\]

L’équation de propagation de la dilatation \(\theta\) a donc la même forme que dans le cas des fluides, la célérité des ondes planes étant : \[c=\sqrt{\frac{\lambda+2~\mu}{\rho}}\]

En prenant maintenant le rotationnel de l’expression précédente, nous obtenons (en remarquant que tout gradient a un rotationnel nul) : \[\rho~\frac{\partial^2[\overrightarrow{\rm rot}(\overrightarrow{u})]}{\partial t^2}=\mu~\Delta[\overrightarrow{\rm rot}(\overrightarrow{u})]\]

On peut voir immédiatement, en se reportant à la figure précédente que le vecteur rotationnel a pour composantes : \[\Big(\frac{\partial u_3}{\partial x_2}-\frac{\partial u_2}{\partial x_3}\Big)\qquad\text{et permutations}\]

Il représente le double de la rotation d’ensemble autour de A que subit, en plus de sa déformation, la portion de solide entourant A.

On vérifiera par exemple sur la figure que la déformation du parallélogramme \(dx_2~dx_3\), représentée par le glissement \(\alpha'+\alpha''\), est accompagnée d’une rotation d’ensemble (\(\alpha''-\alpha'\)).

Nous représenterons donc cette rotation locale par le vecteur rotation : \[\overrightarrow{\omega}=\frac{1}{2}~\overrightarrow{\rm rot}(\overrightarrow{u})\]

Nous obtiendrons alors l’équation de propagation de la rotation : \[\rho~\frac{\partial^2\overrightarrow{\omega}}{\partial t^2}=\mu~\Delta\overrightarrow{\omega}\]

Cette expression diffère de celle que nous avions obtenue pour la propagation de la dilatation \(\theta\), la célérité dans le cas des ondes planes étant \(c'=\sqrt{\mu/\rho}\).

Nous reconnaissons dans les deux célérités \(c\) et \(c'\) que nous avons obtenues les vitesses de propagation qu’une étude élémentaire nous avait permis de calculer dans le cas des ondes longitudinales et des ondes transversales.

On peut d’ailleurs démontrer que tout champ de vecteurs \(\overrightarrow{u}(x_1,~x_2,~x_3,~t)\) peut être considéré comme résultant de l’addition en tout point et à chaque instant de deux champs de vecteurs dont le premier a un rotationnel nul en tout point, alors que le second a une divergence nulle en tout point.

Décomposons maintenant le vecteur déplacement en deux vecteurs (\(u_l,~u_t\)) satisfaisant à ces conditions soit : \[\overrightarrow{u}=\overrightarrow{u_l}+\overrightarrow{u_t} \qquad\text{avec~:}\quad \overrightarrow{\rm rot}(\overrightarrow{u_l})=0\quad\text{et}\quad \rm div(\overrightarrow{u_t})=0\]

Étudions séparément la propagation des deux déplacements.

2.1. Ondes longitudinales

Posons \(\overrightarrow{u}=\overrightarrow{u_l}\) dans l’équation générale de propagation. Elle devient, en remplaçant \(\theta\) par \(\rm div(\overrightarrow{u_l})\)  : \[\rho~\frac{\partial^2u_l}{\partial t^2}=(\lambda+\mu)~\overrightarrow{\rm grad}~\rm div(\overrightarrow{u_l})+\mu~\Delta\overrightarrow{u_l}\]

Rappelons l’identité vectorielle : \[\Delta\overrightarrow{u}=\overrightarrow{\rm grad}[\rm div(\overrightarrow{u})]-\overrightarrow{rot}[\overrightarrow{\rm rot}(\overrightarrow{u})]\]

Par ailleurs : \[\overrightarrow{\rm rot}(\overrightarrow u_l)=0\]

Il vient donc : \[\rho~\frac{\partial^2u_l}{\partial t^2}=(\lambda+2\mu)~\Delta\overrightarrow{u_l}\]

Les ondes planes se propagent à la célérité : \[c=\sqrt{\frac{\lambda+2~\mu}{\rho}}\]

Considérons une telle onde plane et dirigeons l’axe \(Ox_1\) suivant la normale aux plans d’onde. La condition \(\overrightarrow{rot}(\overrightarrow u_l)=0\) permet d’affirmer que \(\overrightarrow{u_l}\) s’identifie à un gradient et que, par suite, la vitesse \(\partial\overrightarrow{u_l}/\partial t \) dérive d’un potentiel comme c’était le cas pour les ondes dans les fluides.

Dans le cas de notre onde plane, \(\overrightarrow{u_l}\) ne dépend que de \(x_l\) et de \(t\). Il en est de même du potentiel des vitesses dont les surfaces équipotentielles sont les plans \(x_1=cte\) et l’on se trouve en présence d’une onde longitudinale.

2.2. Ondes transversales

Faisons maintenant \(\overrightarrow{u}=\overrightarrow{u_t}\), avec \(\rm div(\overrightarrow{u_t})=0\). La dilatation \(\theta=\rm div(\overrightarrow{u_t})\) est nulle en tout point et l’équation de propagation s’écrit alors : \[\rho~\frac{\partial^2\overrightarrow{u_t}}{\partial t^2}=\mu~\Delta\overrightarrow{u_t}\]

Les ondes planes se propagent à la célérité \(c'=\sqrt{\mu/\rho}\).

Dirigeons l’axe \(Ox_1\) suivant la normale aux plans d’onde : le vecteur \(\overrightarrow{u_t}\) étant le même en tout point d’un plan d’onde \(x_1=cte\) à chaque instant, nous aurons : \[\frac{\partial\overrightarrow{u_t}}{\partial x_2}=0\quad\text{et}\quad \frac{\partial\overrightarrow{u_t}}{\partial x_3}=0\]

La condition \(\rm div(\overrightarrow{u_t})=0\) alors alors, en affectant l’exposant \(i\) aux composantes suivant \(Ox_1\) : \[\frac{\partial u_t^1}{\partial x_1}=0\qquad\text{puisque :}\quad \frac{\partial u_t^2}{\partial x_2}=\frac{\partial u_t^3}{\partial x_3}\]

D’autre part : \[\frac{\partial u_t^1}{\partial x_2}=\frac{\partial u_t^1}{\partial x_3}=0\]

Il en résulte \(\Delta u_t^1=0\), puis \(\cfrac{\partial^2u_t^1}{\partial t^2}=0\) d’après l’équation de propagation.

La partie oscillante de \(\overrightarrow{u_t}\) ne comporte pas de composante suivant \(Ox_1\) et se trouve couchée dans le plan d’onde ; l’onde \(\overrightarrow{u_t}\) est une onde transversale.

Nous retrouvons bien le résultat déjà obtenu à savoir que les solides peuvent propager :

1. des ondes longitudinales (compressions et dilatations), la célérité des ondes planes étant : \(c=\sqrt{(\lambda+2\mu)/\rho}\) ;

2. des ondes transversales (rotations et glissements), la célérité des ondes planes étant : \(c'=\sqrt{\mu / \rho}\).