1. Caractéristiques de l’onde associée
On savait déjà, depuis les travaux de Planck sur l’équilibre thermique du rayonnement et d’Einstein sur l’effet photoélectrique, qu’on ne peut expliquer les interactions d’un rayonnement électromagnétique de fréquence \(\nu\) avec la matière qu’en admettant qu’il transporte des photons d’énergie : \[E=h~\nu\qquad;\qquad~h=6,62\times 10^{-34}~J~s\]
D’après la relativité restreinte, tout corpuscule d’énergie E a une masse \(m=E/c^2\) .
S’il s’agit d’un photon, sa vitesse est celle de la lumière \(c\) et son impulsion est : \[p=m~c=\frac{E}{c}=\frac{h~\nu}{c}\]
La longueur d’onde du rayonnement électromagnétique qui l’accompagne est : \[\lambda=\frac{c}{\nu}=\frac{h}{p}\]
Pour l’onde de Louis de Broglie, associée à un électron en mouvement, la fréquence et la longueur d’onde sont liées à l’énergie et à l’impulsion de l’électron comme dans le cas de l’onde lumineuse et du photon : \[\nu=\frac{E}{h}\qquad;\qquad\lambda=\frac{h}{p}\]
1.1. Vitesse de phase et vitesse de groupe
Soit v la vitesse de l’électron ; son énergie relativiste totale est : \[E=m~c^2=\frac{m_0~c^2}{\sqrt{1-\beta^2}}\qquad;\qquad~\beta=\frac{v}{c}\]
La vitesse de phase, c’est-à-dire la vitesse à laquelle la phase de l’onde se propage dans l’espace, est : \[v_{\varphi}=\lambda~v=\frac{E}{p}=\frac{m~c^2}{m~v}\qquad;\qquad~v_{\varphi}=\frac{c^2}{v}~>~c\]
Ainsi la vitesse de phase est-elle supérieure à celle de la lumière.
La vitesse de phase ci-dessus est fonction de la vitesse des électrons, c’est-à-dire de leur énergie, donc de la fréquence de l’onde. Si nous associons à un faisceau d’électrons qui ne peut pas être rigoureusement monocinétique un groupe d’ondes analogues à un signal, l’énergie se propage avec la vitesse de groupe \(v_g\) de ce signal.
Par définition : \[v_g=\frac{d\nu}{d(1/\lambda)}\]
On a successivement :
\[\begin{aligned} \nu=\frac{E}{h}=\frac{m~c^2}{h}\quad\Rightarrow\quad~d\nu&=\frac{c^2}{h}~dm\\ \lambda=\frac{h}{p}=\frac{h}{m~v}\quad\Rightarrow\quad~\frac{1}{\lambda}&=\frac{m~v}{h}\\ d\Big(\frac{1}{\lambda}\Big)&=\frac{1}{h}~(m~dv+v~dm)\end{aligned}\]
D’où une première expression globale de \(v_g\) : \[v_g=\frac{c^2~dm}{m~dv+v~dm}=\frac{c^2}{v+m~\cfrac{dv}{dm}}\]
Partant de la relation : \[m=\frac{m_0}{\sqrt{1-\cfrac{v^2}{c^2}}}=m_0~(1-\frac{v^2}{c^2})^{-1/2}\]
Il vient pour la dérivée : \[\frac{dm}{dv}=\frac{m_0~v}{c^2}~(1-\frac{v^2}{c^2})^{-3/2}\]
Et tous calculs faits : \[v_g=\frac{c^2}{\cfrac{c^2-v^2}{v}+v}=v\]
Résultat très remarquable.
2. Diffraction des électrons
Un électron, accéléré par une différence de potentiel U assez faible pour que l’approximation newtonienne soit valable acquiert une énergie cinétique : \[E=\frac{m~v^2}{2}=e~U\]
La longueur d’onde associée est alors : \[\lambda_0=\frac{h}{m_0~v}=\frac{h}{\sqrt{2~m_0~e~U}}\]
En remplaçant \(h,~m_0\) et \(e\) par leurs valeurs, on trouve : \[\lambda(\text{nm})\approx\sqrt{1,5/U}\approx~1,225/\sqrt{U(\text{volts})}\]
Pour U = 150 V, on a \(\lambda\) = 0,1 nm, une longueur d’onde qui correspond aux rayons X moyens.
Pour U = 15 000 V, on a \(\lambda\) = 0,01 nm, une longueur d’onde qui correspond aux rayons X durs.
Ces longueurs d’onde, comme celles des rayons X correspondants sont de l’ordre de grandeur des distances inter-atomiques dans les cristaux. On doit donc pouvoir obtenir des phénomènes d’interférences entre électrons diffractés par les différents atomes d’un cristal comme cela avait déjà été fait auparavant pour les rayons X.
Si la vitesse de l’électron n’est plus négligeable par rapport à celle de la lumière, on doit tenir compte de l’impulsion relativiste.
L’énergie de l’électron est : \[E=e~U=(m-m_0)~c^2\quad\Rightarrow\quad~m=m_0~\Big(1+\frac{e~U}{m~c^2}\Big)\]
Pour alléger les calculs, nous poserons : \(K=\cfrac{e~U}{m~c^2} \)
D’après la relation d’Einstein : \[\frac{v^2}{c^2}=1-\frac{m_0^2}{m^2}\quad\Rightarrow\quad~v=\frac{c}{1+K}~\sqrt{K^2+2K}\]
Et tous calculs faits : \[\lambda=\frac{\lambda_0}{\sqrt{1+K/2}}\approx\lambda_0~\Big(1-\frac{K}{2}\Big)\approx\lambda_0~\Big(1-\frac{e~U}{4m_0~c^2}\Big)\]
3. Manifestation expérimentale de l’onde associée
L’expérience de Davisson et Germer (1927) qui étudiaient la répartition angulaire des électrons secondaires provenant d’une cible de nickel bombardée par un pinceau d’électrons monocinétiques a fourni une preuve critique qui confirme l’hypothèse de De Broglie postulant que les particules, comme les électrons, pouvaient se comporter comme des ondes.
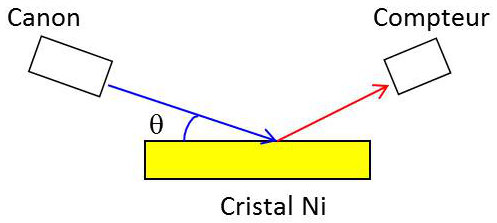Cette répartition dépendait de la structure cristalline de la cible. Si le pinceau frappe un cristal unique de nickel, il y a des maximums d’intensité très prononcés dans certaines directions. Ils dépendent de l’orientation du cristal et de l’énergie du faisceau primaire, donc de la longueur d’onde associée.
La vérification de la formule de Broglie a été entreprise par plusieurs physiciens au moyen de la diffraction d’un pinceau d’électrons monocinétiques par une préparation polycristalline.
On obtient sur une plaque photographique perpendiculaire au faisceau incident des anneaux de diffraction comme dans la méthode de Debie – Scherrer avec les rayons X.
Signalons que Davison et Germer obtenaient des réflexions sélectives, c’est-à-dire que, comme pour les rayons X se réfléchissant sur deux plans réticulaires, les conditions de Bragg doivent être vérifiées : \[2d~\sin\theta=k~\lambda\qquad\text{k entier, ordre de réflexion sélective}\]
4. Optique électronique
On remplace le faisceau de lumière par un faisceau d’électrons. On sait que si l’électron est accéléré par une différence de potentiel U on peut lui associer, en négligeant les effets relativistes, une longueur d’onde : \[\lambda=\frac{h}{\sqrt{2~m~e~U}}\]
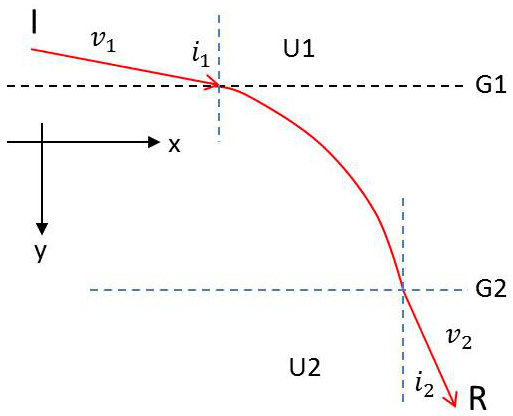On est ainsi amené à rechercher un indice de réfraction comme cela a été fait en optique géométrique. On considère ainsi deux grilles \(G_1\) et \(G_2\). Au-dessus de \(G_1\) règne un potentiel \(U_1\) et au-dessous de \(G_2\) un potentiel \(U_2\).
Un électron, lancé avec une vitesse \(\overrightarrow{v}_1\) faisant un angle \(i_1\) avec la normale à \(G_1\) traverse \(G_1\) puis \(G_2\). Il ressort avec une vitesse \(\overrightarrow{v}_2\) dans la région \(U2\) l’angle avec la normale à \(G_2\) étant \(i_2\) .
Dans les régions \(U_1\) et \(U_2\), les trajectoires sont des droites, l’électron n’étant soumis à aucune force. Par contre, dans la partie située entre les grilles, il existe une différence de potentiel et la trajectoire est une parabole, par analogie avec le mouvement de l’électron dans un condensateur. Les vecteurs \(\overrightarrow{v}_1\) et \(\overrightarrow{v}_2\) sont d’ailleurs tangents à cette trajectoire.
À l’entrée et à la sortie de l’ensemble des deux grilles, il y annulation de la composante horizontale de la vitesse : \[v_1~\sin(i_1)=v_2~\sin(i_2)\]
Or, on a : \[e~U=\frac{1}{2}~m~v^2\]
D’où l’on déduit : \[v_1=\sqrt{\frac{2~e}{m}}~U_1\quad;\quad~v_2=\sqrt{\frac{2~e}{m}}~U_2\]
On obtient donc : \[U_1~\sin(i_1)=U_2~\sin(i_2)\]
On remarque la forte analogie avec les lois de Descartes (identité : \(\sqrt{U}\))
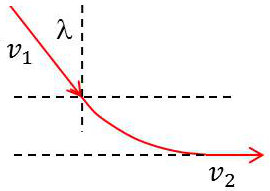
On peut même envisager l’existence d’un angle limite \(\lambda\) conduisant à la réflexion totale. On écrit en effet : \[v_1~\sin(\lambda)=v\]
Il vient : \[e(U_2-U_1)=\frac{1}{2}~(v^2-v_1^2)=\frac{1}{2}~m~v_1^2~\{\sin^2(\lambda)-1\}\]
D’autre part : \[\frac{1}{2}~m~v_1^2=e~U_1\quad\text{et}\quad~e~U_2=e~U_1~\sin^2(\lambda)\]
On a donc : \[\sin(\lambda)=\frac{\sqrt{U_2}}{\sqrt{U_1}}\]
Résultat analogue à celui obtenu en optique géométrique. Il est donc possible de concevoir une optique électronique à base de lentilles électrostatiques ou électromagnétiques, se comportant comme les lentilles que nous connaissons.
4.1. Description sommaire du microscope électronique
On a représenté ci-dessous le schéma du microscope électronique comparé à celui du microscope classique. Les lentilles sont magnétiques et les réglages des inductions magnétiques intervenant dans le mouvement des électrons se font au moyen de potentiomètres (les bobines sont représentées en coupe) :
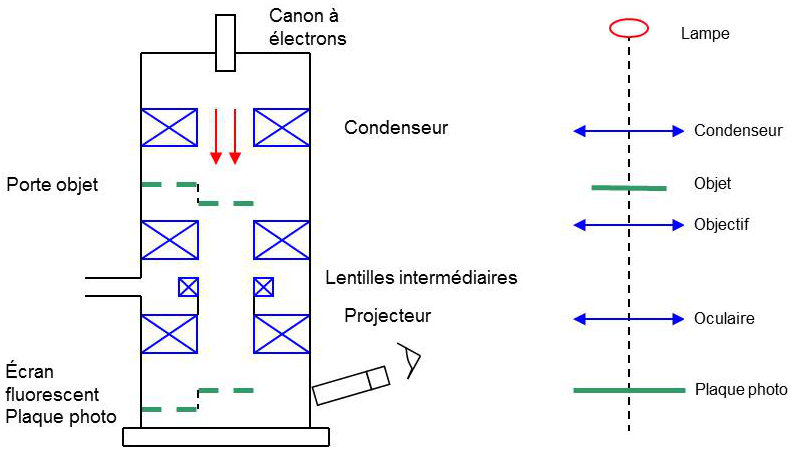
4.2. Avantages du microscope électronique
Le microscope électronique est doué d’un plus grand pouvoir séparateur.
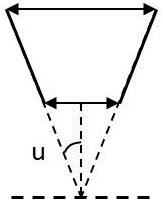On sait en effet que le pouvoir séparateur est donné par l’expression : \[AB=\frac{1,22~\lambda}{2n~\sin(u)}\]
Et l’on a ici : \[\lambda=\frac{h}{m~v}\]
Donc, on diminue \(\lambda\) en augmentant \(v\).
Les meilleurs pouvoirs séparateurs du microscope classique sont de l’ordre de \(0,1~\mu m\) alors qu’ils atteignent facilement des valeurs de l’ordre de 0,5 nm dans le cas du microscope électronique.
Remarque
En optique géométrique, le passage d’un indice à l’autre se faisait de manière discontinue.
En optique électronique, le réglage potentiométrique permet de passer continûment de l’indice \(k\sqrt{U_1}\) à l’indice \(k\sqrt{U_2}\).
Les réglages les plus importants se font au moyen des lentilles intermédiaires.
5. Diffraction des protons et des neutrons
Des expériences ont été faites pour mettre en évidence des phénomènes d’interférences par diffraction d’autres particules, chargées ou non (protons, ions en général, atomes, molécules neutres, neutrons, etc.).
Ces expériences ont permis de mesurer dans chaque cas la longueur d’onde associée aux particules diffractées et ont confirmé la validité de la formule de de Broglie (qui ne fait pas intervenir du reste la charge de la particule, d’où le fait de penser à des particules nouvelles).
Le proton étant chargé positivement est dévié par les champs électriques et magnétiques. En raison de sa grande masse, on pouvait obtenir des longueurs d’onde beaucoup plus courtes que celles de l’électron.
Le microscope photonique a donc un pouvoir de résolution encore plus important que le microscope électronique. À signaler toutefois l’importance de l’absorption et de la diffraction du proton par la matière.
Production de neutrons monocinétiques
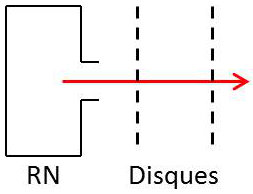Les neutrons sont produits par le réacteur nucléaire RN devant lequel sont disposés des disques D percés tournant à une certaine vitesse.
Pour qu’un neutron puisse passer, il faut que le temps mis par le neutron pour aller d’un disque à l’autre soit égal au temps qui s’écoule entre le passage de deux trous devant le canon.
6. La fonction d’onde. Interprétation physique
Un phénomène ondulatoire est caractérisé par une fonction d’onde, fonction des coordonnées et du temps, qui oscille en chaque point et dont l’oscillation se propage. C’est le cas par exemple des vecteurs \(\overrightarrow{E}\) et \(\overrightarrow{H}\) de l’onde électromagnétique.
Pour une onde électromagnétique, le carré du module de la fonction d’onde \(\overrightarrow{E}\) en un point de l’espace est proportionnel au flux d’énergie tombant sur un écran placé en ce point donc au nombre de photons reçus par cet écran, les photons ayant tous la même énergie.
Par analogie, le carré \(|\Phi|^2\) en tout point de l’espace du module de la fonction d’onde associée à un faisceau d’électrons sera proportionnel au nombre d’électrons reçus par un récepteur placé en ce point.
Pour interpréter les expériences sur ces électrons individuels, nous admettrons que \(\Phi~\Phi^*\) est proportionnel à la probabilité pour un électron d’être à l’instant \(t\) dans un élément de volume \(d\tau\) autour du point (x, y, z).
La quantité \(\Phi~\Phi^*~d\tau\) sera égale à cette probabilité si elle satisfait à la condition de normalisation (probabilité totale égale à 1) : \[\int\limits_{Espace}\Phi~\Phi^*~d\tau=1\]
7. Le principe d’incertitude d’Heisenberg
Le principe s’énonce ainsi :
Il n’est pas possible de connaître avec une précision illimitée deux variables conjuguées telles que \(x\) et \(p_x=m~v_x\).
Les incertitudes \(\Delta x\) et \(\Delta p_x\) sur ces deux variables étant liées par la condition : \[\Delta x~\Delta p_x\geq h\]
Microscope d’Heisenberg
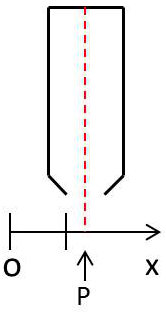Ce principe a pu être élaboré à l’aide d’une observation au microscope.
On cherche à repérer la coordonnée \(x\) d’un corpuscule M. L’observation est limitée par le pouvoir de résolution : \[\Delta x=\frac{1,22~\lambda}{2~n~\sin(u)}\]
Nous poserons : \[\Delta x\approx \frac{\lambda}{\sin(u)}\]
\(u\) est l’angle d’ouverture du microscope.
On voit que \(\Delta x\) sera d’autant plus petit que \(\lambda\) sera petite.
Le photon qui a frappé M s’engage dans le microscope et parvient à l’observateur ; cependant, en raison de l’effet Compton, le corpuscule M s’est déplacé et le photon a été diffusé.
Le photon ayant une impulsion : \[p=\frac{h~\nu}{c}=\frac{h}{\lambda}\]
on voit que p est d’autant plus grande que \(\lambda\) sera petite. Il en résulte que l’impulsion communiquée à M sera plus grande.
La répulsion qui vient troubler le mouvement du corpuscule n’est pas exactement connue puisque la direction du photon est indéterminée dans le faisceau de rayons dont l’angle d’ouverture est \(u\).
L’erreur possible sur la composante suivant \(Ox\) de la quantité de mouvement communiquée au corpuscule sera : \[\Delta p_x=p~\cos\Big(\frac{\pi}{2}-u\Big)=\frac{h}{\lambda}~\sin(u)\]
En faisant le produit, on retrouve bien la relation de proportionnalité : \[\Delta x~\Delta p_x~\varpropto~h\]
8. Diffraction d’un photon par un trou
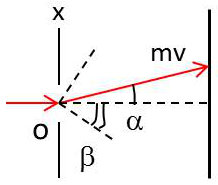L’étude de la diffraction par une fente de largeur \(a\) a montré que l’on observe des maximums d’intensité dans les directions \(\theta\) telles que
\( \sin(\theta)=\cfrac{k~\lambda}{a} \) lorsque l’angle d’incidence est nul.
Le vecteur \(\overrightarrow{p}\) du photon a donc une probabilité d’avoir une direction comprise dans un cône de demi-angle \(\theta\) tel que l’on ait : \[\sin(\theta)=\frac{\lambda}{a}\]
Le vecteur \(\overrightarrow{p}\) peut donc avoir une composante \(p_x\) telle que : \[-p~\sin(\theta)~\leq~p_x~\leq~p~\sin(\theta)\]
La composante \(p_x\) est connue avec une incertitude : \[\Delta p_x\approx p~\frac{\lambda}{a}=\frac{h}{a}\]
Or \(a\) n’est autre que \(\Delta x\). On a donc bien : \[\Delta x~\Delta p_x~\varpropto~h\]
