1. Approche par la mécanique classique

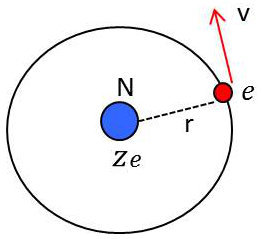La théorie a été élaborée à l’aide de la mécanique classique sur l’atome d’hydrogène et explique l’existence des différents niveaux.

La charge du noyau est \(e\) mais pour un atome quelconque, elle sera \(Z~e\).

L’électron gravitant autour du noyau est soumis à la force attractive : \[f=\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r^2}\]

ceci en supposant le noyau immobile et en ne tenant pas compte des frottements.

D’après la loi des équilibres force centripète – force centrifuge : \[m~\frac{v^2}{r}=m~\omega^2~r=\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r^2}\]

Énergie cinétique : \[E_c=\frac{m~v^2}{2}=\frac{m~\omega^2~r}{2}=\frac{1}{8\pi~\varepsilon_0}~\frac{Z~e^2}{r}\]

Énergie potentielle : \[E_p=-\int f~dr=-\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r}\]

Énergie totale : \[W=E_c+E_p=-\frac{1}{8\pi~\varepsilon_0}~\frac{Z~e^2}{r}\]

D’après la mécanique classique, \(r\) peut prendre toutes sortes de valeurs donc \(W\). Or, il n’en est rien et pour interpréter l’expérience, Bohr postula en 1913 que :

L’atome peut prendre une série discontinue d’états stationnaires dans lesquels il possède une énergie bien déterminée.

Les niveaux d’énergie d’un atome forment une suite discontinue. L’atome peut passer brusquement (saut quantique) d’un état à un autre.

Pour que ce postulat soit satisfait, il faut maintenant sélectionner une suite discontinue de valeurs de \(r\). On est ainsi amené à étudier les conditions de quantification de Bohr.

2. Conditions de quantification de Bohr

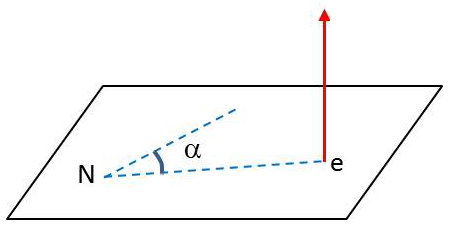Nous savons que \(W=h~\nu\) et qu’il s’agit d’une action.

Bohr a ainsi proposé une intégrale d’action \(\int m~v^2~dt\), prise sur une période de révolution, qui soit égale à un multiple entier de \(h\).

On a :

\[\begin{aligned} v&=r~\frac{d\alpha}{dt}\\ \int_C m~v^2~dt&=\int_0^{2\pi}~m~v~r~d\alpha=2\pi~m~v~r\end{aligned}\]

D’où la condition : \[2\pi~m~v~r=n~h=2\pi~m~\omega~r\]

Introduisons la condition d’équilibre des forces : \[m~\omega^2~r=\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r^2}\]

L’élimination de \(\omega\) conduit à : \[r=\frac{\varepsilon_0~n^2~h^2}{\pi~Z~e^2~m}\]

Puis : \[W=-\frac{m~Z^2~e^4}{8~\varepsilon_0^2~n^2~h^2}\]

Par ailleurs : \[W=-\frac{R~h~c}{n^2}\]

D’où : \[R=\frac{m~Z^2~e^4}{8~\varepsilon_0^2~h^3~c}\]

Le calcul de \(R\) donne une valeur extrêmement voisine de celle indiquée précédemment.

— Où ça ?

3. Phénomène d’entrainement du noyau

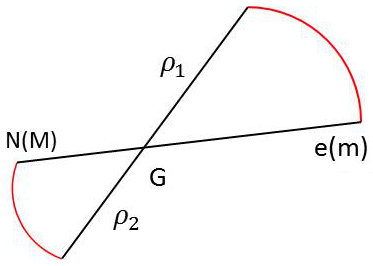Jusqu’à présent, nous avons supposé implicitement que l’électron tourne autour du noyau supposé immobile. Les lois élémentaires de la mécanique classique nous apprennent au contraire que l’ensemble tourne autour de son centre de gravité \(G\).

L’expérience montre du reste que pour deux systèmes hydrogénoïdes dont les noyaux ont des masses différentes, on trouve des valeurs différentes pour la constante \(R\). Il doit donc y avoir entraînement du noyau.

\(G\) étant le barycentre de \(M\) et \(m\) : \[\rho_1~m=\rho_2~M\]

On convient que : \[\rho_1~m=\rho_2~M=\mu~r\quad;\quad r=\rho_1+\rho_2\]

On a : \[\frac{\rho_1}{1/m}=\frac{\rho_2}{1/M}=\frac{\rho_1+\rho_2}{1/m+1/M}=\frac{r}{1/\mu}\]

Par suite : \[\frac{1}{\mu}=\frac{1}{m}+\frac{1}{M}\]

Il n’y a aucun changement pour l’énergie potentielle : \[E_p=-\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r^2}\]

Par contre, pour l’énergie cinétique (rotation autour de G) : \[E_c=\frac{1}{2}~m~\rho_1^2~\varphi'^2+\frac{1}{2}~m~\rho_2^2~\varphi'^2\]

On a donc : \[E_c=\frac{1}{2}~\mu~r^2~\varphi'^2\]

D’où l’énergie totale : \[W=-\frac{\mu~Z^2~e^4}{8~\varepsilon_0^2~n^2~h^2}\qquad\text{avec}\quad\mu=\frac{n~M}{n+M}\]

Remarque

Dans cette théorie le principe d’indétermination d’Heisenberg a été négligé, car à chaque instant on a attribué une position et une vitesse à l’électron.

L’électron et le noyau constituent un dipôle qui produit un champ électrique variable. Si l’électron tourne autour du noyau, il va produire de l’énergie. Si cette énergie est absorbée, il faut que l’électron se rapproche du noyau. La trajectoire telle qu’elle a été décrite ne peut être stable.

4. Intervention de la mécanique ondulatoire

Nous ne tiendrons pas compte de l’entraînement du noyau. Nous cherchons les solutions de l’équation de Schrödinger : \[-\frac{\hbar^2}{2m}~\Delta\Psi+V~\Psi=W~\Psi\]

• \(\Psi\) : Fonction d’onde attachée à l’électron

• \(W\): Énergie totale

• \(V\) : Énergie potentielle de l’électron plongé dans le champ du noyau

On a : \[\overrightarrow{F}=-\overrightarrow{grad(V)}=-\frac{\partial\overrightarrow{V}}{\partial r}=-\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r^2}\]

Par suite : \[V=-\frac{1}{4\pi~\varepsilon_0}\frac{Z~e^2}{r}\]

L’équation de Schrödinger s’écrit alors : \[-\frac{\hbar^2}{2m}~\Delta\Psi-\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r}~\Psi=W~\Psi\]

Pour résoudre cette équation, l’emploi des coordonnées sphériques est tout indiqué. On cherchera alors des solutions de la forme : \[\Psi(\theta,\varphi,r)=F(\theta)~G(\varphi)~H(r)\]

La fonction ainsi trouvée mesure la probabilité de trouver un électron au point de coordonnées (\(r,\theta,\varphi\)).

De manière plus rigoureuse, la probabilité de trouver un électron dans un élément de volume \(dv\) entourant ce point est \(dp=\Psi~\Psi^*~d\Psi\).

Les conditions de normalisation doivent être respectées \[\int_{-\infty}^{+\infty}\Psi~\Psi^*~dv=1\]

La fonction d’onde \(\Psi\) doit converger et ne doit pas être identiquement nulle.

\(W\) ne peut prendre qu’un certain nombre de valeurs et on trouve comme précédemment : \[W=-\frac{\mu~Z^2~e^4}{8~\varepsilon_0^2~n^2~h^2}=-\frac{R~h~c}{n^2}\]

5. Moment dipolaire

Pour étudier le rayonnement, il faut associer deux fonctions d’onde correspondant à deux niveaux différents.

Au premier correspond \(\Psi_1\), donc \(\Phi_1\), et au deuxième correspondra \(\Psi_2\), donc \(\Phi_2\).

On sait par ailleurs que : \[W=h~\nu\quad\Rightarrow\quad \nu=\frac{W}{h}\]

On a :

\[\begin{aligned} &\Phi_1=\Psi_1(r)~\exp(-j2\pi~\frac{W_1}{h}~t)\\ &\Phi_2=\Psi_2(r)~\exp(-j2\pi~\frac{W_2}{h}~t)\end{aligned}\]

On montre qu’en associant ces deux fonctions, on peut trouver la distance moyenne de l’électron au noyau : \[\overline{x}=\int\Phi_2^*(x)~\Phi_1^*~dv\]

Le moment dipolaire sera : \[\overline{e~x}=\int\Phi_2^*~(e~x)~\Phi_1^*~dv\]

D’où : \[\overline{e~x}=\int\Psi_2^*~(e~x)~\Psi_1~\exp(j2\pi~\frac{W_2-W_1}{h}~t)~dv\]

En associant deux niveaux d’énergie stable, on voit apparaître un moment dipolaire.

La condition pour qu’il y ait transition d’un niveau à un autre est que \(\Psi_2^*~(e~x)~\Psi_1\neq 0\).

6. Problème de la dégénérescence

L’équation de Schrödinger ne présente de solutions valables que pour une suite \(\{W_1,~W_2,~\dots\}\) d’énergies.

Pour une même énergie, on peut trouver plusieurs solutions indépendantes \(\{\Psi_1,~\Psi_2,~\dots\}\), donc une infinité de solutions possibles.

Si l’on ne trouve qu’une solution unique, on ne peut trouver qu’un électron décrit par la fonction d’onde ; on dit alors que \(W\) est un niveau dégénéré.

Dans le cas de la dégénérescence, \(W\) étant imposé, la fonction d’onde n’est pas complètement déterminée ; il faut alors imposer d’autres paramètres comme le moment cinétique.

6.1. Moment cinétique

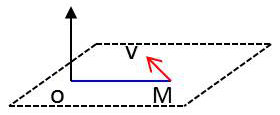Le moment cinétique est le vecteur : \[\overrightarrow{G}=\overrightarrow{OM}\wedge\overrightarrow{mV}=\overrightarrow{OM}\wedge\overrightarrow{P}\]

Avec : \[OM= \left| \begin{aligned} x\\ y\\ z \end{aligned} \right. \qquad P= \left| \begin{aligned} p_x\\ p_y\\ p_z \end{aligned} \right. \qquad G_z=x~p_y-y~p_x\]

On a déjà rencontré : \[p_x~:~\quad\frac{\hbar}{j}~\frac{\partial}{\partial x}~\Psi=p_x~\Psi\]

À \(G_z\) correspondra l’opérateur : \[[G_z]=x~\frac{\hbar}{j}~\frac{\partial}{\partial y}-y~\frac{\hbar}{j}~\frac{\partial}{\partial x}\]

On peut alors écrire : \[\Big\{x~\frac{\hbar}{j}~\frac{\partial}{\partial y}-y~\frac{\hbar}{j}~\frac{\partial}{\partial x}\Big\}~\Psi=G_z~\Psi\]

On démontre que cet opérateur commute avec l’opérateur hamiltonien.

\(\Psi\) est fonction propre des deux opérateurs définis par :

\[\begin{aligned} \Big\{-\frac{\hbar^2}{2m}~\Delta+V\Big\}~\Psi&=W~\Psi\qquad;\qquad V=-\frac{1}{4\pi~\varepsilon_0}~\frac{Z~e^2}{r}\\ \Big\{x~\frac{\hbar}{j}~\frac{\partial}{\partial y}-y~\frac{\hbar}{j}~\frac{\partial}{\partial x}\Big\}~\Psi&=G_z~\Psi\end{aligned}\]