1. Propagation de la lumière dans deux milieux. Lois de Snell-Descartes

Les milieux traversés par la lumière sont supposés homogènes et isotropes. On considère deux milieux séparés par une surface S (surface dioptrique).

Un faisceau lumineux monochromatique (incident) cheminant dans le milieu (1) vient frapper la surface de séparation S.

Deux cas peuvent se produire :

• la lumière est renvoyée en totalité dans le milieu (1) ;

• la lumière est renvoyée en partie dans le milieu (1), tandis que l’autre partie pénétrant dans le milieu (2).

Dans le milieu(1), il s’agit de réflexion du faisceau.

Dans le milieu (2), il s’agit de réfraction du faisceau.

Les lois de Snell-Descartes ont pour objet de préciser la position des rayons réfléchi et réfracté en fonction de celle du rayon incident et de la surface.

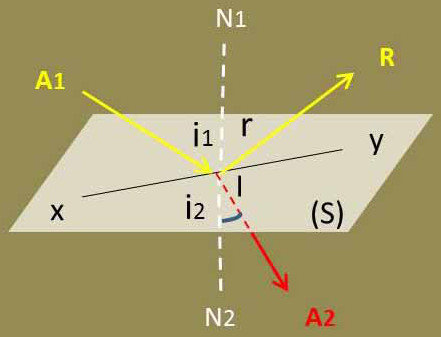Les rayons réfléchis et réfractés sont situés dans le plan d’incidence.

L’angle d’incidence et l’angle de réflexion sont égaux et de sens contraire : \[r~=~-i_1\]

Il existe un rapport constant entre les sinus des deux angles (incidence et réfraction) : \[\frac{\sin(i_1)}{\sin(i_2)}~=~n_{2/1}\]

Ce rapport constant qui, pour la radiation envisagée, dépend des deux milieux consécutifs considérés, s’appelle indice relatif du milieu (2) par rapport au milieu (1) pour cette radiation.

2. Signification physique de l’indice

Les expériences de Foucault pour comparer les vitesses de propagation de la lumière respectivement dans l’air et dans l’eau ont montré que, pour une radiation donnée : \[\frac{V_{air}}{V_{eau}}~=~n_{eau/air}\]

Cette relation, venue de l’observation, a une justification théorique que nous mettrons plus tard en évidence et en application.

2.1. Notion d’indice absolu

Pour une radiation donnée, l’indice absolu d’une substance est par définition son indice par rapport au vide. L’indice absolu \(n_1\) est le rapport des vitesses de la lumière dans le vide et dans ce milieu (1), par exemple : \[n_1~=~\frac{c}{V_1}\]

Comme c’est dans le vide que la lumière se propage le plus vite, les indices absolus sont des nombres toujours supérieurs à 1.

Il résulte de la définition de l’indice absolu que : \[n_{2/1}~=~\frac{V_1}{V_2}~=~\frac{c}{V_2}\cdot\frac{V_1}{c}~=~\frac{n_2}{n_1}\] Plus généralement : \[n_{2/1}~=~\frac{n_{2/3}}{n_{1/3}}\] L’indice relatif de deux milieux est égal au rapport de leurs indices relatifs par rapport à une même substance.

3. Principe du retour inverse de la lumière

Dans la relation de Snell-Descartes, remplaçons l’indice par son expression en fonction des vitesses de propagation. Il vient : \[\frac{\sin(i_1)}{V_1}~=~\frac{\sin(i_2)}{V_2}\]

Cette relation est symétrique.

Elle ne dépend que des deux milieux et non du sens de propagation.

Si au rayon incident \(A_1I\) correspond le rayon réfracté \(IA_2\) lorsque la lumière passe du milieu (1) au milieu (2), alors et inversement, au rayon incident \(A_2I\) dans le milieu (2) correspondra le rayon réfracté \(IA_1\) dans le milieu (1).

C’est le principe du retour inverse de la lumière.

Ce principe peut paraître trivial, mais il s’avère très utile dans certains cas de figure compliqués.

4. Système optique

Un système optique est un ensemble de milieux transparents et homogènes, disposés à la suite les uns des autres et séparés par des surfaces de forme géométrique généralement simple (plan, sphère, paraboloïde) pour qu’il soit facile de les réaliser mécaniquement par génération géométrique.

Les systèmes optiques que nous étudierons sont formés de milieux isotropes. Si, comme cela a lieu en général, les surfaces dioptriques successives sont de révolution autour d’un même axe, le système est dit centré et cet axe est l’axe du système centré.

Si le système ne comporte pas de surface réfractante, il est dit catoptique (miroirs et combinaisons de miroirs). S’il ne contient pas de surface réfléchissante, le système est dioptrique (microscope, la lunette astronomique). Il est dit catadioptrique s’il comporte à la fois des surfaces réfléchissantes et des surfaces réfractantes.

5. Image réelle. Image virtuelle

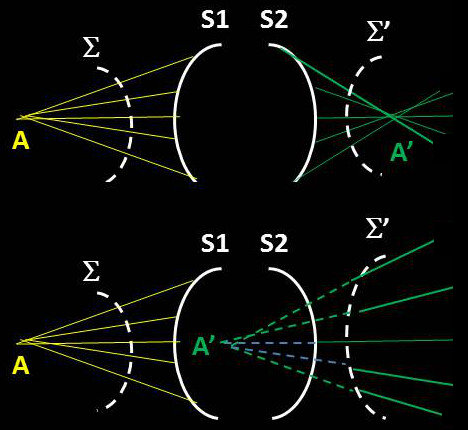Soit un système optique dans lequel ne figurent que les faces externes. La face \(S_1\) qui est du côté du point lumineux A et qui reçoit les rayons venant de ce point est la face d’entrée ; l’autre \(S_2\) est la face de sortie.

Très souvent les faces d’entrée et de sortie sont baignées par le même milieu, à savoir l’air ; il peut toutefois arriver (microscope à immersion) que les milieux qui sont en contact avec les faces d’entrée et de sortie soient différentes.

Le point lumineux A envoie sur \(S_1\) un faisceau de rayons coniques divergent. Si ce point est convenablement placé par rapport au système, certains de ses rayons traversent \(S_1\), pénètrent dans le système optique, cheminent à travers lui et sortent par \(S_2\) formant un faisceau émergent.

La forme de ce faisceau émergent dépend de la constitution du système optique et de la position de A. Si ce faisceau est conique de sommet A’, on dit que le système optique donne du point lumineux A une image A’.

Il faut distinguer deux cas, suivant le faisceau émergent :

• le faisceau conique émergent est convergent, les rayons qui le constituent passent alors réellement par A’. On dit que A’ est l’image réelle de A ;

• le faisceau conique est divergent ; le point A’ est alors situé sur le prolongement des rayons émergents, sur leur partie virtuelle. A’ est alors une image virtuelle.

Supposons l’image A’ réelle :

Plaçons notre œil au-delà de A’ et regardons dans la direction de A’. Si l’œil se trouve à l’extérieur du faisceau conique ouvert sortant, nous ne verrons pas A’ puisque aucun rayon ne venant de ce point ne tombe sur lui. Si l’œil est à l’intérieur du faisceau sortant et à une distance suffisante de A’ (supérieure à la distance de vision distincte), nous verrons le point A’ qui sera pour nous un véritable point lumineux.

Supposons l’image A’ virtuelle :

Si l’œil, regardant dans la direction de A’ est placé à l’extérieur du faisceau émergent, nous ne verrons rien. S’il est placé à l’intérieur du faisceau sortant et assez loin, nous aurons l’impression qu’il y a en A’ un véritable point lumineux.

Un observateur peut donc, à condition de placer son œil dans le faisceau sortant, au-delà de l’image et assez loin, apercevoir cette image, et pour lui rien ne distingue une image virtuelle d’une image réelle.

Dans les deux cas, il voit en A’ un point lumineux, que ce point existe réellement (image réelle) ou qu’il n’existe pas (image virtuelle).

Coupons par un écran diffusant (feuille de papier, verre dépoli, toile blanche ou aluminée tendue, écran perlé etc.) le faisceau sortant du système, puis éloignons progressivement l’écran de la face de sortie. Si l’image A’ est virtuelle, nous obtiendrons sur l’écran une tache lumineuse (section du faisceau par l’écran, rendue visible grâce à la lumière diffusée par l’écran) qui va s’agrandissant.

Si l’image A’ est réelle, la tache va au contraire en se rapetissant, et à un moment donné, lorsque l’écran passera par A’, nous verrons sur l’écran un point lumineux. Nous dirons qu’à ce moment l’écran reçoit l’image A’. Une image réelle peut donc être reçue sur un écran, ce qui permet de la rendre visible à un observateur placé n’importe où devant l’écran. Une image virtuelle ne peut être reçue sur un écran.

5.1. Étude d’un système composé

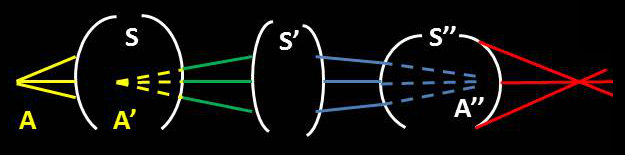Ces notions de réalité et de virtualité des points objets et images étant extrêmement importantes, nous donnons ci-dessous un exemple de système composé. Nous y rencontrons trois systèmes successifs S, S’, S" centrés sur un même axe, baignant dans le même milieu et représentés par leurs faces d’entrée et de sortie.

• A est un point réel pour le système S.

• A’ est l’image virtuelle que S donne de A.

• A’ se comporte pour S’ comme un point objet réel.

• S’ donne de A’ une image réelle A" qui joue pour S" le rôle d’objet virtuel.

• S" donne de A" une image réelle A’’’.

L’ensemble des trois systèmes optique donne du point lumineux réel A (objet) une image réelle A’’’.

6. Stigmatisme

Soit un système optique S donnant d’un point lumineux A (réel ou virtuel) une image (réelle ou virtuelle), l’application du principe du retour inverse de la lumière nous montre que si, le système travaillant en sens inverse, A’ devenait le point lumineux (réel ou virtuel), il aurait pour image à travers le système le point A (réel ou virtuel). Pour traduire cette réciprocité, on dit que les deux points A et A’ sont conjugués par rapport au système optique.

On verra qu’il est assez difficile, sauf dans des cas très particuliers, d’obtenir que tous les rayons partant du point A passent rigoureusement en A’. Lorsque cette condition est réalisée, on dit qu’il y a stigmatisme pour le couple de points A et A’, ou encore que le système est stigmatique pour les points A et A’.

6.1. Stigmatisme approché

Les systèmes centrés que nous aurons l’occasion d’étudier, exception faite pour le miroir plan, sont loin d’être stigmatiques pour tous les points de l’espace objet. Heureusement que l’œil est, lui aussi, un instrument imparfait ; sa constitution est telle que l’image d’un point, donnée par un système optique, nous paraît acceptable, même si elle n’est pas rigoureusement ponctuelle.

De même les écrans qui reçoivent les images réelles, la plaque photographique qui fixe de telles images, ont une structure discontinue. La plaque photographique par exemple est formée d’éléments sensibles (grains d’émulsion) juxtaposés : un élément frappé par la lumière est tout entier impressionné. L’image d’un point sera donc parfaite pour la plaque même, si ses dimensions atteignent sans les dépasser celles du grain sensible.

Nous dirons alors qu’un système optique est approximativement stigmatique pour un couple de points AA’, s’il transforme le faisceau conique incident de sommet A en un faisceau dont les rayons viennent passer très près d’un même point A’ (par exemple, à l’intérieur d’un petit élément de volume entourant A’).

Le système travaillant en sens inverse transformerait un faisceau conique incident de sommet A’ en un faisceau dont tous les rayons viendraient passer à l’intérieur d’un petit élément de volume entourant A.

Alors que les systèmes centrés ne sont en général rigoureusement stigmatiques que pour un couple de points de leur axe, ils sont approximativement stigmatiques pour une étendue notable de l’espace objet à laquelle ils font correspondre une certaine étendue de l’espace image.