1. Introduction aux systèmes centrés

Une association convenable de dioptres et de miroirs permet de former un système centré. Si l’on se limite aux rayons paraxiaux, chacune des surfaces fonctionnera dans l’approximation de Gauss et donnera d’un petit objet plan perpendiculaire à l’axe une petite image également perpendiculaire à l’axe.

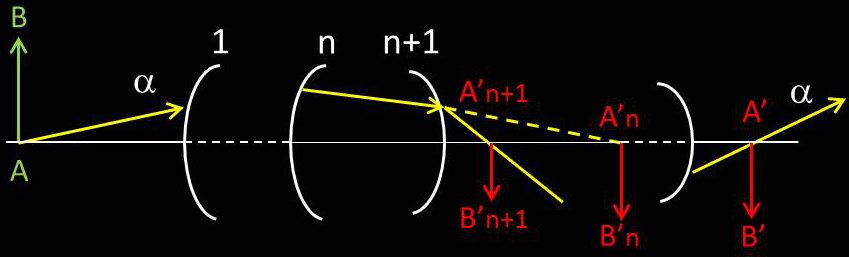L’application des formules de conjugaison et de grandissement à chacune des surfaces successives fournira la position et la grandeur de l’image définitive, l’image fournie par la N-ième surface devenant l’objet pour la (n+1)-ième. Il y a donc simplement un problème d’élimination des variables intermédiaires.

Nous devons faire deux remarques permettant d’éviter ces calculs fastidieux :

1. La relation entre les abscisses de l’objet et de l’image dans chaque surface étant une relation homographique, la relation entre la position de l’objet et celle de l’image dans l’instrument complet est encore une relation homographique.

   Il ne sera donc pas étonnant que l’on puisse caractériser géométriquement un système centré par des points singuliers de cette homographie.

2. L’invariant de Lagrange-Helmoltz étant conservé à la traversée de chaque surface, il sera conservé entre l’espace objet et l’espace image de l’instrument. On devra donc écrire (p désignant le nombre de miroirs rencontrés) :

\[n'y'\alpha'~=~(-1)^p~n~y~\alpha\]

Nous devons maintenant étudier les éléments géométriques caractéristiques des systèmes centrés que nous appellerons éléments cardinaux :

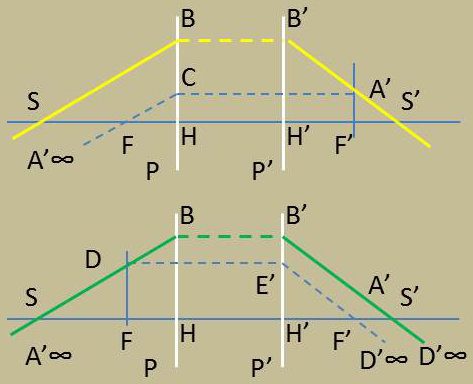
1. Tout point de l’axe a une image qui est aussi un point de l’axe, et à une position A du point objet correspond une position et une seule A’ du point image. En particulier, lorsque le point A est à l’infini, le point A’ occupe une position particulière, bien définie F’, qui est le foyer image du système.

   De même, la relation homographique objet – image définit une position F de l’objet telle que l’image A’ soit à l’infini. F est le foyer objet du système. Le système a donc un foyer objet et un seul F, un foyer image et un seul F’.

2. Tout plan objet perpendiculaire à l’axe et passant par A a pour image un plan perpendiculaire à l’axe et passant par A’.

   De tels plans sont dits conjugués. En particulier, le plan objet à l’infini a pour conjugué le plan focal image (plan mené par F’ perpendiculairement à l’axe) et le conjugué du plan focal objet (plan perpendiculaire à l’axe passant par F) est le plan normal à l’axe à l’infini.

Les plans focaux ont les propriétés suivantes :

1. Un pinceau incident isogène dont le sommet est dans le plan focal objet donne, à l’émergence, un pinceau de rayons parallèles.

2. Un pinceau de rayons incidents parallèle donne à l’émergence un pinceau isogène dont le sommet est dans le plan focal image.

NB : Un faisceau lumineux est dit isogène lorsque tous les rayons passent par un même point.

Les plans focaux sont généralement à distance finie et l’on dit que le système est un système à foyers. Cependant, de nombreux systèmes optiques (en particulier les instruments destinés à observer les objets éloignés) donnent d’un objet à l’infini une image également à l’infini ; les foyers sont alors rejetés à l’infini dans les deux espaces extrêmes et sont alors conjugués l’un de l’autre. De tels systèmes sont appelés systèmes afocaux.

2. Systèmes à foyers

2.1. Plans principaux

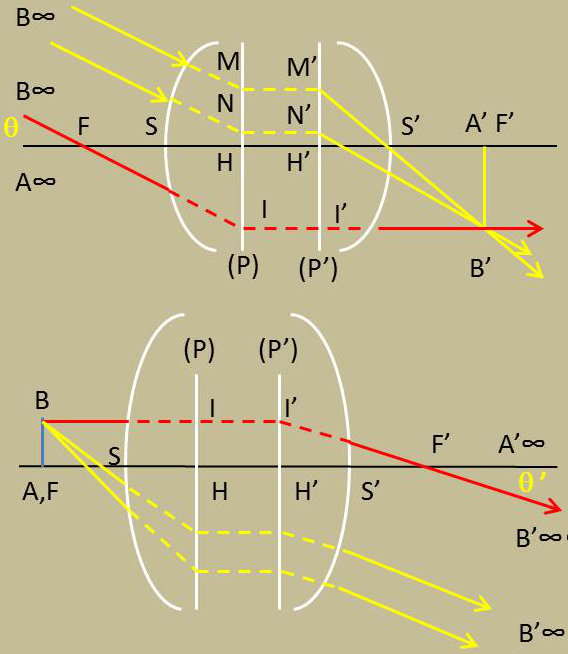
On appelle plans principaux deux plans conjugués pour lesquels le grandissement linéaire est égale à +1.

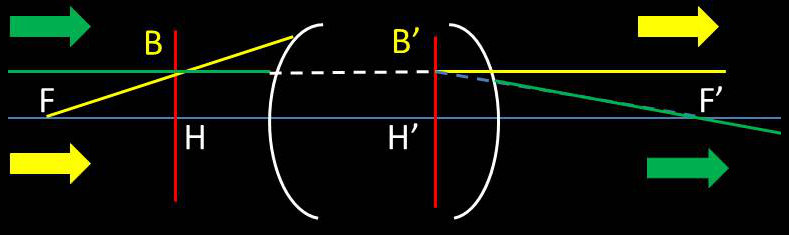Lorsqu’un objet AB est dans le plan principal objet, son image A’B’ est dans le plan principal image ; elle est droite et égale à AB.

Il n’y a qu’un seul couple de points principaux.

Avec le sens adopté pour la lumière incidente, P est le plan principal objet, P’ est le plan principal image. En faisant travailler le système en sens inverse, on permute les deux plans principaux.

L’incident MB parallèle à l’axe, qui perce en B’ le plan principal image P’ a pour émergent le rayon B’F’. B’ est un point commun à ces deux rayons.

On peut donc dire que : Le plan principal image est le lieux des points de rencontre des supports des rayons incidents parallèles à l’axe avec les supports des rayons émergents correspondants (ces derniers passant par le foyer image).

On verrait de même que : Le plan principal objet est le lieu des points de rencontre des supports des incidents qui passent par le foyer objet avec les supports des rayons émergents qui leur correspondent (ces derniers sont parallèles à l’axe).

Note

Il ne faut pas en déduire que le lieu de l’intersection d’un incident parallèle à l’axe et de l’émergent est un plan quelle que soit la distance du rayon incident à l’axe ; ce lieu est en fait une surface de révolution (souvent une sphère) qui est assimilable à son plan tangent au voisinage de son pôle (dans l’approximation de Gauss).

2.2. Distances focales

Les points H et H’ où les plans principaux coupent l’axe sont dits points principaux. Ces points sont dits conjugués : H est le point principal objet, H’ est le point principal image.

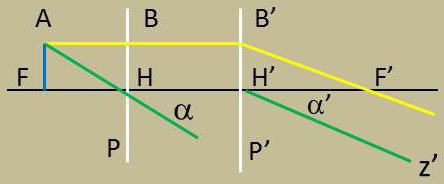On appelle distance focale objet du système l’abscisse du foyer objet par rapport au point principal objet ; c’est le segment \(\overline{HF}=f\).

On appelle distance focale image l’abscisse du foyer image par rapport au point principal image ; c’est le segment \(\overline{H'F'}=f'\).

Dans la figure ci-contre, considérons un point A du plan focal objet.

Un rayon parallèle à l’axe mené à partir de A percera les plans principaux respectivement en B et B’. Naturellement H’B’ est l’image de HB et on a : \[\overline{H'B'}~=~\overline{HB}\]

Le rayon incident AH fait avec l’axe l’angle \(\alpha\). Son émergent H’z’ passe par H’ et fait avec l’axe un angle \(\alpha'\) .

L’application de la formule de Lagrange-Helmoltz aux points conjugués H et H’ permet d’écrire : \[n~\overline{HB}~\alpha~=~n'~\overline{H'B'}~\alpha \qquad \text{ou}\qquad n~\alpha~=~n'\alpha'\]

Les deux angles sont donc de même signe. Comme \(\alpha<0\), il en est de même de \(\alpha'\). La demi droite H’z’ doit, en partant de H’ se diriger vers le bas. Tous les rayons issus de A sortant parallèlement à la direction H’z’, le rayon émergent qui correspond à l’incident AB s’obtiendra en menant par B’ la parallèle B’F’ à H’z’ ; le point F’ où elle coupe l’axe est le foyer image ; il est à droite de H’.

Nous trouvons donc ici que la distance focale image est positive ; or, la distance focale objet a été supposée négative. Si la distance focale objet avait été prise positive, nous aurions trouvé une distance focale image négative : Les distances focales d’un système dioptrique centré sont toujours de signes contraires.

Dans les triangles respectifs AHF et B’HF’ :

\[\begin{aligned} \overline{FA} &~=~\overline{HF}~\alpha\\ \overline{H'B'}&~=~-\overline{H'F'}~\alpha'\end{aligned}\]

D’où : \[f~\alpha~=~f'\alpha'\]

Comme on a vu que : \[n~\alpha~=~n'\alpha'\]

On en déduit la relation fondamentale : \[\frac{f}{f'}~=~-\frac{n}{n'}\]

Le rapport des distances focales est égal au rapport, changé de signe, des indices des milieux extrêmes.

Nous retrouvons là une propriété des distances focales déjà rencontrées dans le dioptre sphérique.

Si les milieux extrêmes sont identiques, les distances focales sont égales et opposées. Les deux foyers sont disposés symétriquement par rapport au milieu du segment HH’.

Le système optique sera dit convergent s’il transforme un faisceau cylindrique incident parallèle à l’axe en un faisceau émergent convergent. Il sera dit divergent si ce même faisceau incident sort du système en divergent.

2.3. Applications des propriétés des foyers et des plans principaux

2.3.1. Construction de l’image d’un point B situé en dehors de l’axe

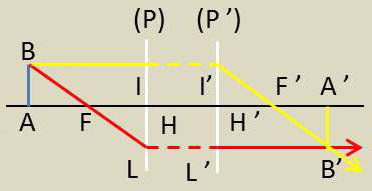
Pour avoir l’image B’ de B, il faut mener deux incidents issus de B et tracer les émergents correspondants. Nous choisissons :

• le rayon incident BI parallèle à l’axe ; il perce en I’ le plan principal image et sort suivant F’ :

• le rayon incident BF qui passe par le foyer objet F ; il perce le plan principal objet en L ; son émergent est Lx, parallèle à l’axe mené par L.

Les deux rayons émergents sz coupent en B’ qui est l’image cherchée.

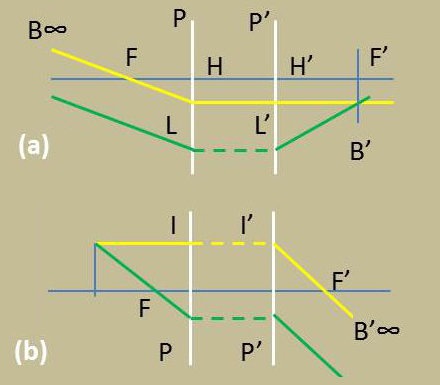Deux cas particuliers sont intéressants :

1. Le point B est à l’infini : son image B’ est dans le plan focal image.

   Un seul rayon incident suffit pour déterminer B’ ; nous prendrons le rayon BF qui perce en L le plan principal objet et sort parallèlement à l’axe suivant Lx. Le point d’intersection de L et du plan focal image est le point B’ cherché.

2. Le point B est dans le plan focal objet : son image est à l’infini, dans une direction que nous déterminerons en considérant l’incident BI parallèle à l’axe ; il perce en I’ le plan principal image et sort suivant I’F’. Le point B’ est à l’infini sur la droite I’F’

2.3.2. Construction d’un émergent correspondant à un incident donné

a) Le rayon issu de S rencontre le plan principal objet en B. On en déduit le point B’ dans le plan principal image.

C’est un point du rayon émergent. Pour en trouver un deuxième, admettons que l’incident provient du point A situé à l’infini sur son support.

L’image A’ de A est dans le plan focal image et se détermine comme il vient d’être dit : à l’incident FC venant de A (FC parallèle à SB) correspond le réfracté CA’ parallèle à l’axe qui perce en A’ le plan focal image.

L’émergent recherché est alors B’A’.

b) Nous pouvons admettre que le rayon incident SB est émis par le point D où il perce le plan focal objet. Le rayon émergent passe par l’image D’ de D.

On la détermine comme nous venons de le voir en menant par D le rayon parallèle à l’axe qui perce en E’ le plan principal image et sort suivant E’F’. Le point D’ est à l’infini sur E’F’. Le rayon cherché s’obtient en menant par B la parallèle à E’F’.

2.3.3. Construction de l’image A’B’ d’un objet plan perpendiculaire à l’axe

On construit l’image B’ du point B qui est en dehors de l’axe, puis on abaisse de B’ la perpendiculaire B’A’ sur cet axe.

a) Objet à l’infini

Diamètre apparent \(\theta\). Un faisceau de rayons est issu de B. L’image est dans le plan focal image.

On voit que : \[A'B'~=~-f~\theta\]

b) Objet dans le plan focal

L’image est à l’infini. Sa construction se fait sans difficulté.

Cette image A’B’ est vue sous un angle : \[\theta'~=~\frac{AB}{f'}\]

c) Position de l’objet quelconque

La figure explique clairement cette construction.

L’image du point A est située sur l’axe. Un rayon issu de B et parallèle à l’axe convergera vers le foyer image F’ en sortie du système. À contrario, un rayon issu de B et passant par le foyer objet F sera parallèle en sortie du système.

Les deux rayons issus de B se coupent en B’ qui est le point cherché. On en déduit la position de A’.

2.4. Formules de conjugaison et de grandissement

La construction de l’image à l’aide des rayons passant par les foyers F et F’ est strictement identique à celle que nous avons rencontrée dans l’étude du dioptre sphérique si ce n’est que les plans principaux H et H’ ne sont plus en coïncidence, mais ceci n’influe manifestement pas sur la nature des formules de conjugaison, à condition de prendre des origines H ou F dans l’espace objet, H’ ou F’ dans l’espace image.

On voit donc a priori que les formules de conjugaison sont les mêmes que dans le dioptre. Nous allons les retrouver très simplement.

2.4.1. Origines aux foyers (formules de Newton)

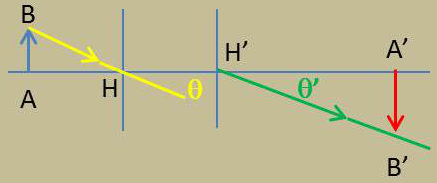
On se réfère à la figure précédente pour le cas (c).

Posons : \[\overline{HF}=f \quad;\quad \overline{FA}=\sigma \quad;\quad \overline{F'A'}=\sigma' \quad;\quad \overline{H'F'}=f'\]

Dans les triangles semblables ABF et FHL :

\[\begin{aligned} &\frac{y'}{y}=\frac{\overline{HL}}{\overline{AB}}=\frac{\overline{FH}}{\overline{FA}}=-\frac{f}{\sigma}\\ &\frac{y'}{y}=\frac{\overline{A'B'}}{\overline{H'T'}}=\frac{\overline{F'A'}}{\overline{F'H'}}=-\frac{\sigma'}{f'}\end{aligned}\]

On peut donc écrire : \[\frac{y'}{y}=-\frac{f}{\sigma}=-\frac{\sigma'}{f'} \quad\Rightarrow\quad \sigma~\sigma'=f~f'\]

Ces formules sont bien les mêmes que pour un seul dioptre.

Leur discussion conduirait à des résultats identiques. En particulier : \[\sigma=f \quad\Rightarrow\quad \sigma'=f'\quad\text{et}\quad\gamma=+1\]

Nous retrouvons les plans principaux.

2.4.2. Origines aux points principaux

Posons :

\[\begin{aligned} x~&=~\overline{HA}~=~f+\sigma \\ x'~&=~\overline{H'A'}~=~f'+\sigma'\end{aligned}\]

En revenant à la relation de Newton : \[f~x'+f'x~=~x~x'\]

En tenant compte de la relation première : \[\frac{f}{f'}=-\frac{n}{n'}\]

En utilisant le paramètre : \[D=-\frac{n}{f}=\frac{n'}{f'}\]

La relation de conjugaison s’écrit alors : \[\frac{n'}{x'}-\frac{n}{x}~=~D\]

Le grandissement se détermine en utilisant le rayon BH qui sort suivant H’B’. Nous avons déjà établi la relation : \[n'\theta'=n~\theta\]

Il vient : \[\frac{y'}{y}~=~\frac{\theta'x'}{\theta~x}~=~\frac{n}{n'}~\frac{x'}{x}\]

2.5. Notion de convergence

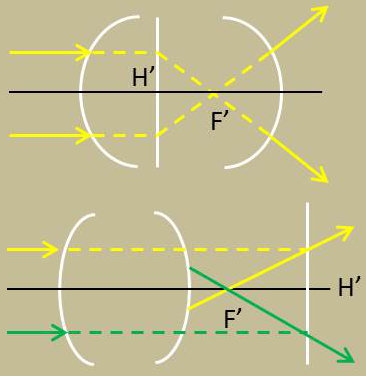Par analogie avec le cas des lentilles minces, on dira qu’un système est convergent lorsque sa distance focale image \(\overline{H'F'}=f'\) est positive.

Il est divergent dans le cas contraire. On caractérisera la convergence par le paramètre D.

Remarquons que le signe de D n’implique rien sur la nature des foyers. Par exemple, un système convergent peut avoir un foyer image virtuel et donner un faisceau divergent à partir de ce foyer.

Inversement, un système divergent peut donner un faisceau convergeant vers un foyer F’ réel.

2.6. Grandissement

On a rencontré le grandissement transversal : \[\gamma_y=\frac{y'}{y}=\frac{n}{n'}\frac{x'}{x}\]

exprimé à l’aide des paramètres \(\sigma,~\sigma'\) ou \(x,~x'\).

2.6.1. Grandissement linéaire

\[\gamma_{\alpha}=\frac{\alpha'}{\alpha}\]

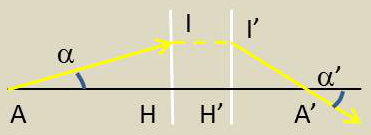D’après la relation de Lagrange : \[\frac{n'}{n}~\gamma_y~\gamma_x=1\quad\Rightarrow\quad\gamma_{\alpha}=\frac{x}{x'}\]

On aurait pu démontrer directement cette relation en écrivant : \[\alpha~x=\alpha' x'=-\overline{HI}=-\overline{H'I'}\]

2.6.2. Grandissement axial

\[\gamma_x=\frac{dx'}{dx}\]

Par différentiation des relations de conjugaison :

\[\begin{aligned} \sigma~\sigma'=f~f' &\quad\Rightarrow\quad \sigma~d\sigma'+\sigma'~d\sigma=0 \quad\Rightarrow\quad \gamma_x=\frac{d\sigma'}{d\sigma}=-\frac{\sigma'}{\sigma}\\ \frac{n'}{x'}-\frac{n}{x}=D &\quad\Rightarrow\quad \gamma_x=\frac{dx'}{dx}=\frac{n}{n'}~\frac{x'^2}{x^2}\end{aligned}\]

D’où la relation générale entre les trois agrandissements : \[\gamma_y=\gamma_{\alpha}~\gamma_x\]

2.7. Points nodaux

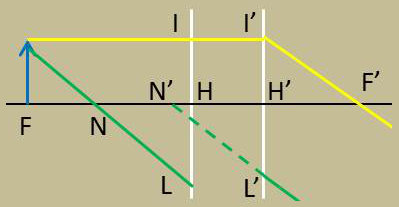Lorsqu’un incident et son émergent sont parallèles, leurs supports coupent l’axe en deux points fixes N et N’ appelés points nodaux.

Soit B un point quelconque du plan focal objet.

Tous les incidents dont les supports passent par B donnent des émergents parallèles entre eux.

Leur direction commune est donnée par le rayon BII’ qui sort du système suivant IF’.

Menons par B la parallèle BNL à IF’ ; le rayon incident dont le support est BNL sort parallèlement à lui-même suivant N’L’.

Les points N et N’ sont donc les points nodaux. Ces points sont fixes et sont en particulier indépendants du point B choisi pour les obtenir.

En effet, les triangles BFN et H’I’F’ sont égaux et semblablement orientés. On a donc : \[\overline{FN}=\overline{H'F'}=f=\text{cste}\]

Comme le point F est fixe, il en est de même de N. Le point N’, conjugué de N par rapport au système est également fixe. N est le point nodal objet. N’ est le point nodal image.

Les triangles HLN et H’L’N’ étant égaux et semblablement orientés nous avons : \[\overline{H'N'}=\overline{HN}=\overline{HF}+\overline{FN}=\overline{HF}+\overline{H'F'}=f+f'\]

Donc : \[\overline{F'N'}=\overline{H'N'}-\overline{H'F'}=f+f'-f'=f\]

Dans le parallélogramme LL’N’N : \[\overline{NN'}=\overline{LL'}=\overline{HH'}\]

La distance des points nodaux est égale à la distance des points principaux. Cette distance est appelée interstice du système.

Remarque 1

Si comme cela arrive fréquemment, les deux milieux extrêmes sont identiques (\(f'=-f\)), on a alors : \[\overline{HN}=\overline{H'N}=0\]

Les points nodaux sont confondus avec les points principaux.

Remarque 2

Dans le cas du dioptre unique, les deux points principaux sont confondus avec le sommet S du dioptre (pour ce point qui est à lui-même son image, on a \(\gamma=+1\)). Les deux points nodaux sont alors confondus et leur abscisse par rapport au sommet est :

\[\overline{SN}=\overline{SN'}=r\]

Nous retrouvons le centre C du dioptre ; ce résultat est équivalent a priori puisque tout rayon incident, dont le support contient le point C, continue sa route sans être dévié.

Applications des points nodaux à la construction de l’image d’un objet

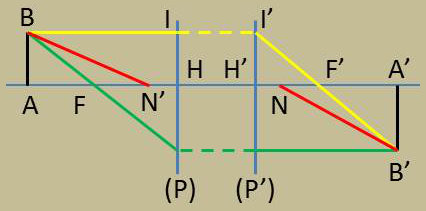Le rayon incident BN donne un émergent qui lui est parallèle et passe par N.

En lui adjoignant un second rayon, soit BI parallèle à l’axe, soit BF. Nous obtenons immédiatement B’ et par suite B’A’.

2.8. Plans antiprincipaux

Les plans antiprincipaux sont les plans de front conjugués pour lesquels le grandissement linéaire est égal à \(-1\). Les points où ils coupent l’axe sont les points antiprincipaux.

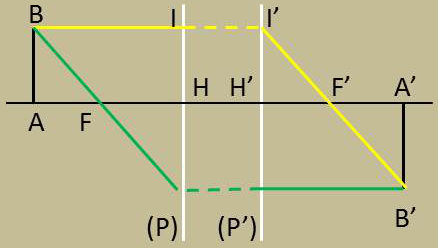Soit BI le rayon incident, parallèle à l’axe issu du point B de l’objet. Ce rayon émerge suivant I’F’ ; l’image A’B’ sera égale à l’objet et renversée si nous plaçons le point A’ de manière que : \[\overline{F'A'}=-\overline{H'F'}=+f'\]

De la position de A’B’, nous déduisons immédiatement la position de AB. Nous voyons que : \[\overline{FA}=\overline{HF}=f\]

Les plans antiprincipaux objet et image sont respectivement symétriques des plans principaux objet et image par rapport aux foyers correspondants.

Remarque

En faisant \(\gamma=-1\) dans les formules de Newton, nous retrouvons immédiatement les abscisses des plans antiprincipaux par rapport aux foyers correspondants \(\overline{FA}=f\) et \(\overline{FA'}=f'\).

2.9. Système centré dont les milieux extrêmes sont identiques

Du point de vue mathématique, le système centré dont les milieux extrêmes sont identiques n’est qu’un cas particulier, mais du point de vue pratique c’est, de beaucoup, le cas le plus fréquent, puisque les instruments d’optique sont le plus souvent en contact avec l’air aux deux extrémités (quelques instruments seulement font exception comme le microscope à immersion).

Rassemblons ici les résultats relatifs à ce cas particulier.

2.9.1. Distances focales égales et opposées

On suppose donc \(f'~=~-f\).

Nous appellerons distance focale (sans qualificatif) du système sa distance focale image. Les formules deviennent : \[\frac{1}{x}-\frac{1}{x'}=\frac{1}{f}\] \[\gamma=\frac{x'}{x}\] \[\sigma~\sigma'=f'^2\] \[\gamma=-\frac{f'}{\sigma}=-\frac{\sigma'}{f}\]

2.9.2. Points nodaux respectivement confondus avec les points principaux

Écriture de la relation de Lagrange-Helmoltz : \[y~\alpha=y'\alpha' \quad \text{ou} \quad \gamma_y=\frac{1}{\lambda_{\alpha}}\]

Grossissement angulaire et grandissement linéaire pour tout couple de points conjugués sont l’inverse l’un de l’autre

Pour tout couple de points conjugués, la relation du grandissement axial au grandissement linéaire est : \[\gamma_x=\gamma_y^2\]

2.10. Système centré catadioptrique

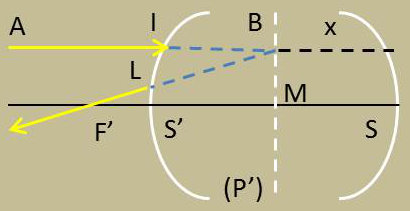Si le système centré contient une surface réfléchissante, il est dit catadioptrique. Cette surface réfléchissante qui sera soit un miroir sphérique centré sur l’axe du système, soit un miroir plan perpendiculaire à cet axe le limite nécessairement d’un côté.

La surface dioptrique S’ qui le limite de l’autre côté est à la fois face d’entrée et face de sortie.

Soit Ax un incident parallèle à l’axe ; ce rayon pénètre en I, se réfracte un certain nombre de fois, se réfléchit, puis se réfracte à nouveau en cheminant en sens inverse et sort en L, sans avoir quitté le plan de la figure.

Le point F’ où le rayon émergent coupe l’axe est le foyer image.

Appliquons au rayon lumineux AI...LF le principe du retour inverse. Nous voyons que l’incident F’L donnera l’émergent IA, F’ est donc aussi le foyer objet. Le système a ses deux foyers confondus.

Prenons le point d’intersection B’ du rayon incident AI parallèle à l’axe et de son émergent LF’. Le front d’onde P’ passant par B’ est le plan principal image. L’application du principe du retour inverse de la lumière nous montre que P’ est aussi le plan principal objet.

Le système catadioptrique qui a ses deux foyers confondus et ses deux plans principaux également confondus est donc équivalent à un miroir sphérique qui aurait son foyer en F’ et son sommet au point M où le plan P’ coupe l’axe.

2.10.1. Sommet du miroir équivalent

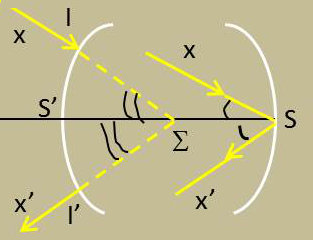Soit un incident XI auquel correspond, dans le milieu en contact avec le miroir sphérique le rayon xS.

Le rayon réfléchi Sx’ est symétrique du précédent et il émerge selon le rayon I’X’ symétrique du rayon entrant.

Le point de rencontre \(\Sigma\) de l’incident XI et de l’émergent I’X’ est à lui-même son image dans le système catadioptrique : c’est un point fixe, et comme tout incident passant par ce point donne un émergent symétrique par rapport à l’axe, \(\Sigma\) est le sommet du miroir équivalent au système catadioptrique.

Si nous remarquons que tout rayon émanant de S sort du système en passant par \(\Sigma\), nous voyons que \(\Sigma\) est l’image de S à travers tout le système antérieur. Pour trouver \(\Sigma\), nous chercherons donc l’image de S fournie par le système dioptrique précédant le miroir en supposant qu’il travaille dans le sens de la lumière réfléchie.

2.10.2. Centre du miroir équivalent

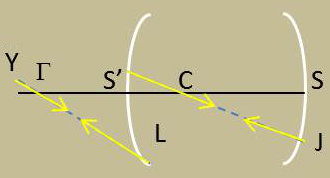Soit YL un incident donnant un rayon CJ qui dans le dernier milieu passe par C centre de la surface réfléchissante. Le rayon CJ se réfléchit sur lui-même et le trajet de retour de la lumière se superpose au trajet aller. L’incident YL donne l’émergent \(L\Gamma\).

Le point \(\Gamma\) où ce rayon coupe l’axe est à lui-même son image dans le système catadioptrique. De plus, à tout incident passant par ce point correspond un émergent ayant même support. \(\Gamma\) est donc le centre du miroir équivalent.

Si nous remarquons que tout rayon émanant de C sort du système en passant par \(\Gamma\), nous voyons que \(\Gamma\) est l’image de C à travers tout le système antérieur. Pour trouver ce point \(\Gamma\), nous chercherons l’image de C donnée par le système dioptrique qui précède le miroir en supposant qu’il travaille dans le sens de la lumière réfléchie.

Exemple

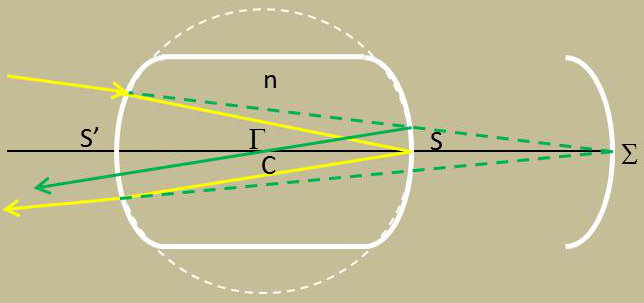Dans une sphère en verre d’indice n découpons un cylindre de révolution dont l’axe coïncide avec un diamètre de la sphère et argentons l’une des faces terminales S.

Proposons-nous de déterminer le miroir équivalent au système catadioptrique ainsi formé.

Le sommet de ce miroir est l’image de S dans le dioptre sphérique S’, celui-ci travaillant dans le sens SS’. Appliquons l’équation de conjugaison rapportée par exemple au sommet S’ du dioptre, nous avons : \[\frac{n}{\overline{S'S}}-\frac{1}{S'\Sigma}~=~\frac{n-1}{r}\]

Remarquant que : \[\overline{S'S}~=~2r\]

Il vient : \[\overline{S'\Sigma}~=~\frac{2r}{2-n}\]

Pour \(n=3/2\), on trouvera \(\overline{S'\Sigma}=4r\).

Le centre \(\Sigma\) est l’image de C dans le dioptre S’, c’est ce point lui-même. Tout problème sur le système proposé se ramène à un problème sur un miroir sphérique placé dans l’air, de sommet \(\Sigma\) et de centre \(\Gamma\). Ce miroir équivalent est un miroir sphérique concave.

3. Systèmes afocaux

Un système est afocal quand les deux foyers sont à l’infini. Il en est ainsi d’un système formé de n dioptres lorsque le foyer image du premier dioptre coïncide avec le foyer objet du système partiel formé par les (n – 1) dioptres suivants ou, plus généralement, lorsque le foyer image du système partiel formé par les p premiers dioptres coïncide avec le foyer objet du système partiel formé par l’ensemble des (n – p) dioptres suivants.

En effet, le foyer image du système est à l’infini, tout incident parallèle à l’axe donne donc un émergent parallèle à l’axe et le foyer objet est aussi à l’infini.

Les systèmes afocaux ont des propriétés très simples :

• Ils donnent d’un objet à l’infini une image à l’infini ; pour cette raison, on les utilisera pour observer les objets éloignés. L’image fournie étant également à l’infini pourra être observée sans accommoder pour un observateur ayant une vue normale.

• Ils n’ont pas de plans principaux.

• Les grandissements sont constants (ils ne dépendent pas de la position de l’objet). C’est évident sur le dessin (parallélisme en entrée et en sortie).

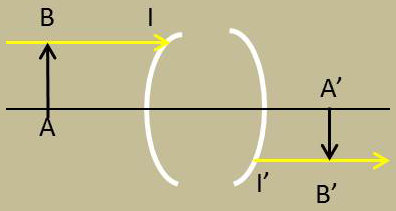On a donc : \[\gamma_y=\frac{A'B'}{AB}=\text{cste}\]

Le grandissement angulaire a pour expression, compte tenu de la relation de Helmoltz-Lagrange : \[\gamma_{\alpha}~\gamma_y=\frac{n}{n'}\]

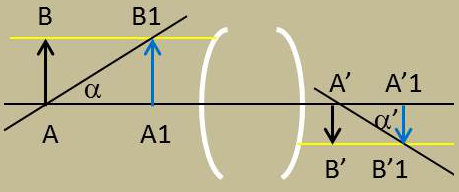Le grandissement axial est constant. Soit en effet AB et \(A_1B_1\) deux positions de l’objet et \(A'B'\) et \(A'_1B'_1\) leurs images.

Soit \(\alpha\) l’angle que fait \(AB_1\) avec l’axe, \(\alpha'\) l’angle correspondant dans l’espace image. La relation de Lagrange s’écrit : \[n~y~\frac{\overline{A_1B_1}}{AA_1}~=~n'y'~\frac{\overline{A'_1B'_1}}{A'A'_1}\]

D’où le grandissement axial : \[\gamma_x=\frac{\overline{A'A'_1}}{\overline{AA_1}}=\frac{n'}{n}\gamma_y^2\]

Il est constant comme \(\gamma_y\).

Cas particulier

Supposons les deux milieux extrêmes identiques (\(n'=n\)). On a alors :

\[\begin{aligned} &\gamma_{\alpha}=\frac{1}{\gamma_y}\\ &\frac{x'}{x}=\gamma_x=\gamma_y^2\end{aligned}\]

Exemples

La lame à faces parallèles est un système afocal. Pour ce système, \(\gamma_y=1\).

Si les milieux qui baignent la lame sur ses deux faces ont des indices différents, on a : \[\gamma_{\alpha}=\frac{n}{n'}\quad;\quad \gamma_x=\frac{n'}{n}\]

Si les deux faces sont baignées dans un même milieu :

\[\begin{aligned} &\gamma_{\alpha}=1 \qquad \text{la lame ne dévie pas les rayons}\\ &\gamma_x=1 \qquad \text{objet et image se déplacent toujours de la même quantité}\end{aligned}\]

Nous retrouvons la constance de la distance de l’objet à son image.

Les lunettes et les télescopes, mis au point sur l’infini pour un œil normal forment des systèmes afocaux.

En conclusion, les propriétés des systèmes afocaux sont simples : les grandissements y sont constants et la relation de conjugaison est linéaire.

4. Association de systèmes centrés

Considérons deux systèmes centrés dont on connaît les éléments cardinaux \(H_1H'_1\), \(H_2H'_2\), \(F_1F'_1\), \(F_2F'_2\) que l’on associe en faisant coïncider leurs axes.

L’ensemble forme un système global dont on peut se proposer de déterminer les éléments cardinaux.

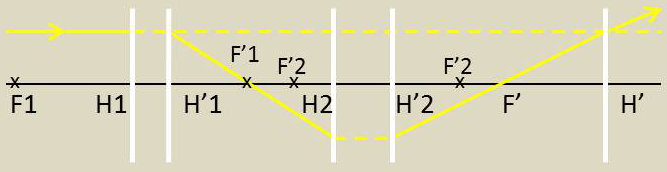Traçons pour cela un rayon incident parallèle à l’axe passant par \(F'_1\) et, après traversée du deuxième système, par le foyer définitif image \(F\).

F sera le conjugué de \(F'_1\) dans le deuxième système, ce que l’on traduira par la relation : \[\overline{F'_2F'}~=~\frac{f_2~f'_2}{\overline{F_2F'_1}}\]

On écrirait de même pour le foyer objet : \[\overline{F_1F}~=~\frac{f_1~f'_1}{\overline{F'_1F_2}}\]

Il reste à déterminer la position des points principaux. La position de H’ peut être déterminée en écrivant des relations de similitude (figure précédente). Mais nous préférons déterminer directement la convergence du système global en utilisant la relation entre la grandeur angulaire d’un objet situé à l’infini et la dimension linéaire de son image.

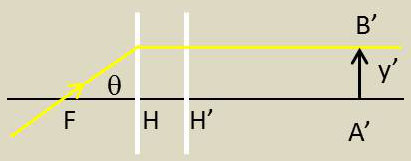Dans un système centré à foyers, on aura : \[y'=A'B'=-f~\theta\]

L’image intermédiaire fournie par le premier système sera : \[y'_1=-f_1~\theta\]

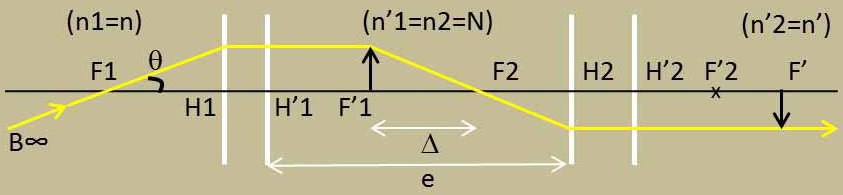Si l’on pose maintenant \(\overline{F'_1F_2}=\Delta\), le grandissement du deuxième système est égal d’après les formules de Newton à \(f_2/{\Delta}\).

L’image définitive F’B’ aura donc comme dimension : \[y'=-\frac{f_1~f_2~\theta}{\Delta}\]

On doit donc avoir : \[f=-\frac{f_1~f_2}{\Delta}\quad~;\quad f'=-\frac{f'_1~f'_2}{\Delta}\]

On peut donc exprimer la convergence du système en fonction de l’intervalle \(H'_1H'_2~=~e\).

On aura : \[\Delta=f_2-f'_1+e\]

Et si l’on fait apparaître les convergences des systèmes : \[D_1=-\frac{n_1}{f_1}\quad;\quad D_2=-\frac{n_2}{f_2}\]

On aura, en calculant D :

\[\begin{aligned} &D=-\frac{n}{f}=D_1+D_2-\frac{e}{N}D_1D_2\\ &N=n'_1=n_2\end{aligned}\]

Cette relation est relation de Gulstrand. Une relation très utile par la suite.