1. Une observation première
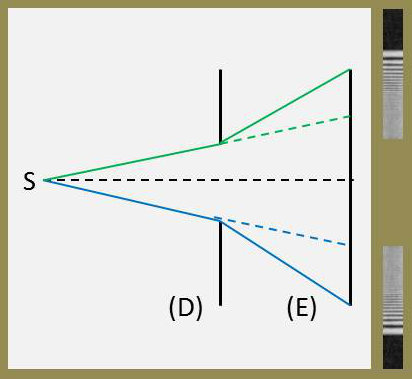Lorsque la lumière, issue d’une source \(S\), arrive sur un diaphragme \(D\), la zone éclairée n’est pas limitée au seul cône d’ombre géométrique. Il n’existe pas non plus de zone immédiatement dans le noir absolu. Il s’opère une sorte d’assombrissement en dégradé.
C’est la manifestation première du phénomène de diffraction que l’on peut considérer comme le comportement des ondes lorsqu’elles rencontrent un obstacle.
Tout se passe comme si la densité de l’onde n’était pas conservée, contrairement aux loi de l’optique géométrique.
2. Types de diffraction
Il existe trois types de diffraction :
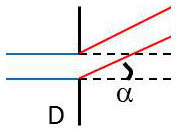
1) La diffraction de Fraunhoffer ou diffraction à l’infini :
La source est située à l’infini et on examine la lumière envoyée à l’infini dans les directions faisant un angle avec la direction rectiligne.
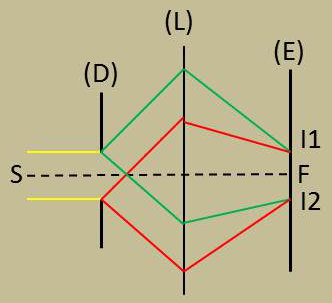
2) La diffraction au voisinage d’un foyer :
Elle nécessite l’utilisation d’une lentille \(L\). Du fait de la diffraction, on observe deux images de \(S\) dans le plan focal de \(L\).
3) La diffraction de Fresnel :
La source et le plan d’observation sont à distance finie. Aucun système optique n’est intercalé entre la source \(S\) et le plan d’observation \(P\).
3. Principe de Huyghens
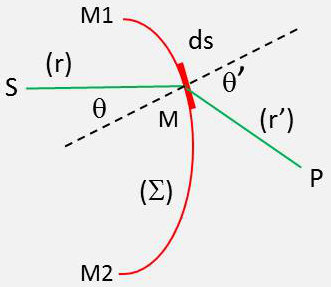Les vibrations se propageant à l’extérieur d’une surface \(\Sigma\) fermée, à l’intérieur de laquelle se trouve une source \(S\) sont identiques à celles que l’on obtiendrait en supprimant cette source et en la remplaçant par des sources convenablement réparties sur \(\Sigma\).
Si la lumière se propage à travers une ouverture \(M_1M_2\) percée dans un écran opaque, pour calculer l’état vibratoire en \(P\), on applique ce principe à une surface \(\Sigma\) limitée par le contour de l’ouverture.
Soit \(A_0\) l’amplitude de la source \(S\) qui envoie sur l’élément de surface \(ds\) la vibration : \[\frac{A_0}{r}~\exp\big(-j~2\pi~\frac{r}{\lambda}\big)\]
À son tour, \(ds\) envoie sur P la vibration : \[K~\Big\{\frac{A_0}{r}~\exp\big(-j~2\pi~\frac{r}{\lambda})~ds\cdot\frac{1}{r'}~\exp\big(-j~2\pi~\frac{r'}{\lambda}\big)\Big\}\]
\(K\) est un facteur qui dépend de \(\lambda,~\theta,~\theta'\). Nous ferons l’hypothèse que \(K\) est constante pour le point de départ des exposés suivants.
