1. Position du problème

Le problème de diffraction le plus simple à étudier est quand le plan d’observation et la source sont situés tous deux à l’infini sans que soit interposé de système optique. L’application du principe de Huyghens est simplifiée : les sources secondaires réparties sur la portion d’onde découverte reçoivent toutes leurs vibrations sous le même angle et émettent également toutes sous le même angle vers le point P.

Le calcul d’interférences fera intervenir les différences de phase des vibrations envoyées au point P par tous les points de l’ouverture. Dans la direction de propagation rectiligne, toutes les différences de phase sont nulles et l’interférence est totalement constructive, mais quand on s’écarte de cette direction, les différences de phase augmentent, l’interférence devient de moins en moins constructive et la résultante devient rapidement négligeable.

Nous exprimerons d’abord les différences de phase, nous écrirons la somme des vibrations (intégration) et nous étudierons ensuite les variations de l’intensité résultante en fonction de l’écart à la direction de propagation rectiligne.

2. Formules générales

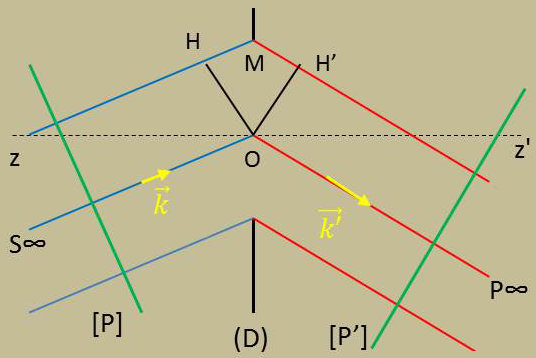La pupille ou diaphragme \((D)\) est représentée en coupe, perpendiculairement à la direction de propagation \(z'z\).

On fixe une origine \(O\) dans l’ouverture que l’on peut rapporter à deux axes \(Ox,Oy\) du plan de \((D)\).

Les deux milieux séparés par \((D)\) sont identiques de sorte que la longueur d’onde est la même des deux côtés.

\((P)\) et \((P')\) sont les plans d’onde, \(\vec{k}\) et \(\vec{k'}\) sont les vecteurs d’onde incidente et réfractée. Les normales aux plans d’onde sont désignés par \(\vec{n}\) et \(\vec{n'}\).

On sait que : \[\overrightarrow{k}=\frac{2\pi}{\lambda}~\overrightarrow{n}\qquad;\qquad \overrightarrow{k'}=\frac{2\pi}{\lambda}~\overrightarrow{n'}\]

Comme origine des phases pour le point \(P\) situé à l’infini, nous prenons celle envoyée par le point \(O\). Celle envoyée par \(M\) aura un retard de marche :

\[\begin{aligned} &\delta=\overline{HM}+\overline{MH'}=\overrightarrow{n}\cdot\overline{OM}+\overrightarrow{n'}\cdot\overline{MO}\\ &\delta=\overline{OM}\cdot(\overrightarrow{n}-\overrightarrow{n'}) =\vec{r}\cdot(\overrightarrow{n}-\overrightarrow{n'})\end{aligned}\]

D’où le déphasage entre vibrations : \[\varphi=\frac{2\pi}{\lambda}~\delta=\overrightarrow{r}\cdot(\overrightarrow{k}-\overrightarrow{k'})\]

2.1. Calcul de l’amplitude

En désignant par \(K.A_0\) l’amplitude diffractée par le point \(O\), celle diffractée par le point \(M\) sera \(K.A_0\exp(-j\varphi)\).

Celle diffractée par un élément de surface \(ds\) entourant le point \(M\) sera : \[K~A_0\exp(-j\varphi)~ds=K~A_0~\exp\{j~\overrightarrow{r}\cdot(\vec{k'}-\overrightarrow{k})\}\]

Et l’amplitude diffractée par l’ouverture sera : \[A(\overrightarrow{k'})=\iint\limits_SK~A_0~\exp\{j~(\overrightarrow{k'}-\overrightarrow{k})\cdot\overrightarrow{r}\}~ds\]

Remarque

Si on place dans l’ouverture une lentille mince, on introduit un déphasage supplémentaire. Si on introduit un milieu absorbant, on modifie à la fois le module et l’argument de A.

On introduit alors dans l’expression un coefficient \(t(\vec{r})\) complexe : c’est le coefficient de transmission de l’amplitude au point M : \[A(\vec{k'})=\iint\limits_S t(\overrightarrow{r})~K~A_0~\exp\{j~(\overrightarrow{k'}-\overrightarrow{k})\cdot\overrightarrow{r}\}~ds\]

De façon à l’exprimer sous forme analytique, on posera : \[\overrightarrow{n} \left\{ \begin{aligned} \alpha\\ \beta\\ \gamma \end{aligned} \right. \qquad \overrightarrow{k} \left\{ \begin{aligned} (2\pi/\lambda)~\alpha\\ (2\pi/\lambda)~\beta\\ (2\pi/\lambda)~\gamma \end{aligned} \right. \qquad \overrightarrow{n'} \left\{ \begin{aligned} \alpha'\\ \beta'\\ \gamma' \end{aligned} \right. \qquad \overrightarrow{k'} \left\{ \begin{aligned} (2\pi/\lambda)~\alpha'\\ (2\pi/\lambda)~\beta'\\ (2\pi/\lambda)~\gamma' \end{aligned} \right. \qquad \overrightarrow{r} \left\{ \begin{aligned} x\\ y\\ 0 \end{aligned} \right.\]

Et l’amplitude aura pour expression : \[A(\alpha',~\beta')=\iint\limits_S K~A_0~\exp\Big\{j~\frac{2\pi}{\lambda}~\big[(\alpha'-\alpha)~x+(\beta'-\beta)~y\big]\Big\}\]

2.2. Calcul de l’intensité

L’amplitude étant connue, on écrit que \(I=A.A^*\) dans le cas le plus général. Si l’expression de l’amplitude est réelle, alors \(I=A^2\).

Enfin si la vibration s’écrit sous la forme d’une somme de deux vibrations en quadrature : \[s(t)=a~\cos(\omega~t)+b~\sin(\omega~t)\]

on a alors : \(I=a^2+b^2\).