1. Objet de phase. Définition

Considérons un objet non lumineux par lui-même. Du point de vue optique, son existence est due à l’action qu’il a sur la lumière : cette action se traduit par le fait que chaque point de l’objet transmet (ou réfléchit) une plus ou moins grande fraction de la lumière incidente, ou par le fait que chaque point introduit une plus ou moins grande différence de phase dans la vibration transmise (ou réfléchie) ou encore par les deux à la fois.

Dans le premier cas, on dit qu’il s’agit d’un objet d’amplitude et dans le deuxième d’un objet de phase. Par exemple, une lame dont l’épaisseur ou dont l’indice de réfraction ne sont pas uniformes et un objet de phase par transmission ; une surface réfléchissante imparfaitement plane est un objet de phase par réflexion.

Les objets d’amplitude sont facilement perceptibles, mais il n’en est pas de même pour les objets de phase alors que c’est le cas le plus important, notamment en biologie où l’on étudie l’homogénéité des tissus.

Si un objet de phase reçoit une onde plane, celle qu’il renvoie n’est plus plane à cause des accidents locaux.

2. Strioscopie

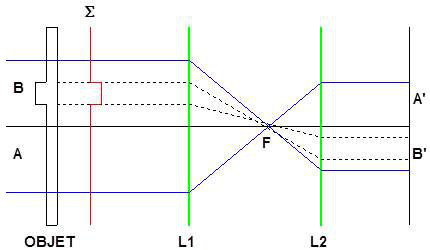Nous supposerons que la lame de verre présente une protubérance \(B\) d’épaisseur \(e\).

En \(B'\), il y aura un retard de phase par rapport à \(A'\) :

– Amplitude reçue en \(A'\) : \(A_0\)

– Amplitude en \(B'\) : \(A_0~\exp(-j\varphi)\) \[\varphi=\frac{2\pi\delta}{\lambda}=\frac{2\pi}{\lambda}~(n-1)~e\]

\(\varphi\) étant supposé très petit, on peut faire l’approximation : \[\exp(-j\varphi)\approx 1-j\varphi=1+\varphi~\exp(-j\pi/2)\]

Si la vibration reçue en \(A'\) est : \[V_1=A_0\cos(\omega t)\]

celle reçue en \(B'\) sera : \[V_2=A_0\cos(\omega t)+\varphi A_0\cos(\omega t-\pi/2)\]

Comme on peut le constater, le terme d’amplitude supplémentaire est proportionnel au défaut de phase.

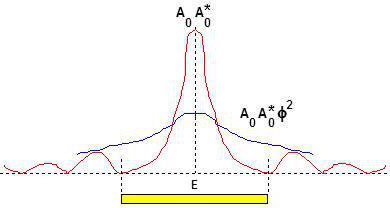L’effet de la protubérance \(B\) sur l’onde est donc d’ajouter à la figure de diffraction en \(F\) due à l’onde \(\Sigma\) non perturbée une autre figure de diffraction due à la protubérance elle-même.

On sait d’ailleurs que ce sont les lentilles qui provoquent des diffractions.

On le voit sur les courbes ci-contre : \[I_1=A_0A_0^*\qquad;\qquad I_2=A_0A_0^*~(1+\varphi^2)\]

La seconde figure de diffraction sera beaucoup plus large que la première parce que nous supposons que la protubérance n’occupe qu’une faible fraction de la surface de la zone. Donc, si on place un petit écran opaque \(E\) ayant pour dimension celle de la tache centrale de diffraction non perturbée, on peut arrêter pratiquement toute la vibration \(A\) en laissant passer la plus grande partie de la vibration \(\varphi A\).

Ainsi, en plaçant en \(F\) un écran \(E\) de dimension convenable, on n’observera plus aucune lumière dans le plan, sauf au point \(B'\) conjugué de \(B\). Ce point \(B'\) apparaît donc brillant sur un fond sombre.

Cette méthode, très utilisée pour étudier les défauts de verre dans les instruments d’optique, présente certains inconvénients :

• Comme on étudie un éclairement proportionnel à \(\varphi^2\), on ne connaît pas le signe de \(\varphi\) et on ne sait pas s’il s’agit d’une bosse ou d’une cavité.

• La méthode est peu sensible pour les faibles valeurs de \(\varphi\), car cette sensibilité \(\sigma=dI/d\varphi\) est proportionnelle à \(\varphi\) et s’annule quand \(\varphi\rightarrow 0\).

• Si la largeur du défaut est trop grande, sa figure de diffraction n’est pas beaucoup plus large que la première, l’écran en prend la majeure partie.

• Si le défaut est trop petit, alors la lumière déborde de la lentille \(L_2\) et une partie de la lumière due au défaut est perdue. L’écran intercepte la tache centrale de la figure de diffraction due à \(\Sigma\) non perturbée ; cependant, les anneaux de diffraction entourant la tache centrale subsistent. Il y a donc un voile diffus dans un plan qui n’est pas complètement obscur.

Remarque

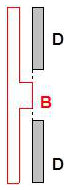Soit \(B\) le domaine de la bosse et \(D\) le domaine total du diaphragme. On a deux vibrations : \(s=s_1+s'_1\) : \[s_1=A_0~\exp(j\omega t)\quad;\quad s'_1=A_0~\exp\{j(\omega t+\varphi)\}\]

\(\varphi\) désignant le déphasage classique obtenu après le calcul de la différence de marche dans les diffractions habituelles.

La vibration totale sera (théorème de Babinet) :

\[\begin{aligned} &s=\int\limits_{D-B}s_1~\exp(j\varphi)+\int\limits_B(s_1+s'_1)~\exp(j\varphi)\\ &s=\int\limits_Ds_1~\exp(j\varphi)+\int\limits_Bs'_1~\exp(j\varphi)\end{aligned}\]

C’est cette dernière formule qui permet de conclure à la superposition des deux figures de diffraction : celle de \(D\) seul et celle de \(B\) seul, cette dernière beaucoup plus plate parce que son amplitude \(\varphi A_0\) est très petite.

3. Contraste de phase. Méthode de Zernike

Au lieu de supprimer la vibration \(A\) par l’écran \(E\), on la déphase de \(\pi/2\) en remplaçant \(E\) par un écran de mêmes dimensions mais transparent et introduisant un retard de marche (en supposant que le défaut est une bosse qui retarde la vibration) de \(\lambda/4\)  : \[(n-1)~e=\frac{\lambda}{4}\quad;\quad e~:\text{ épaisseur de l'écran}\]

En \(B'\), les vibrations \(V_1\) et \(V_2\) sont alors en phase et l’amplitude en \(B'\) et l’intensité deviennent :

\[\begin{aligned} A&=A_0~(1+\varphi)\\ I&=I_0~(1+\varphi)^2\approx I_0~(1+2\varphi)\end{aligned}\]

Ainsi, dans le plan d’observation (\(\pi\)), on verra un éclairement uniforme en absence de l’objet et les défauts de phase se traduisent par des variations de cet éclairement. Un avantage immédiat : \(\varphi\) apparaît avec son signe dans l’expression de l’intensité.

La sensibilité de la méthode dépend des variations relatives d’éclairement que produit l’introduction de \(\varphi\).

D’une façon plus précise, un défaut de phase sera perçu si le contraste \(\gamma\) auquel il donne lieu est supérieur à une certaine limite, liée aux propriétés de l’œil. Il est de l’ordre de 0,1 pour les valeurs de l’éclairement normalement utilisé.

On a ici : \[\gamma=\frac{I-I_0}{I_0}\approx 2\varphi\]

Méthode de Foucault-Zernike

La méthode de Foucault-Zernike consiste à affaiblir et déphaser de \(\pi/2\) l’onde principale.

Le déphasage est dû à la lame de verre L et l’affaiblissement à la couverture métallique M (absorbante) : \[A'=\pm j(kA'_0)-j(\varphi~A'_0)\]

On alors :

\[\begin{aligned} &A'A'^*=A'_0{A'_0}^*~(\pm k-\varphi)^2\\ &A'A'^*=A'_0{A'_0}^*~(k^2 \pm 2k\varphi+\varphi^2)\end{aligned}\]