1. Expérience idéale

1.1. Franges d’interférences rectilignes

Considérons deux sources monochromatiques, de même fréquence mais d’amplitudes différentes.

Supposons en outre que ces sources sont cohérentes entre elles, c’est-à-dire qu’elles sont secondaires dérivées d’une même source primaire.

Supposons également ces deux sources ponctuelles et désignons par \(A_0\) l’amplitude émise par la source primaire \(S\) vers les sources secondaires \(S_1\) et \(S_2\).

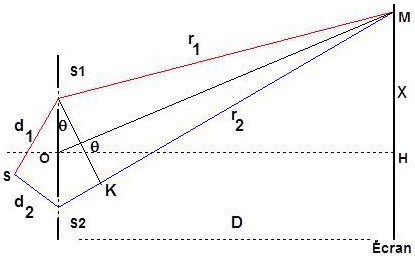
Observons ce qui se passe en un point \(M\) du plan écran, parallèle à \(S_1S_2\) et situé à une distance \(D\) du plan des deux sources.

L’amplitude reçue en \(M\) est la somme des amplitudes émises en \(M\) par les sources \(S1\) et \(S2\) :

\[\begin{aligned} &S_1~:\qquad\frac{A_0}{d_1}~\exp\big(-j~2\pi\frac{d_1}{\lambda}\big)\times\frac{1}{r_1}~\exp\big(-j~2\pi\frac{r_1}{\lambda}\big)\\ &S_2~:\qquad\frac{A_0}{d_2}~\exp\big(-j~2\pi\frac{d_2}{\lambda}\big)\times\frac{1}{r_2}~\exp\big(-j~2\pi\frac{r_2}{\lambda}\big)\end{aligned}\]

Ces deux résultats sont les conséquences directes des théorèmes sur la propagation des vibrations sphériques :

• Amplitude divisée par la distance du point à la source d’émission,

• Déphasage fonction de cette même distance et de la longueur d’onde émise.

Nous poserons pour alléger les écritures (en supposant les grandeurs \(a_i\) réelles) :

\[\begin{aligned} \varphi_1&=\frac{2\pi}{\lambda}~(d_1+r_1) &&\varphi_2=\frac{2\pi}{\lambda}~(d_2+r_2)\\ a_1&=\frac{A_0}{d_1r_1} &&a_2=\frac{A_0}{d_2r_2}\end{aligned}\]

L’amplitude reçue en \(A\) sera: \[A=a_1 \exp(-j\varphi_1)+a_2\exp(-j\varphi_2)\]

D’où l’expression de l’intensité :

\[\begin{aligned} &AA^*=\{a_1\exp(-j\varphi_1)+a_2\exp(-j\varphi_2)\}~\{a_1\exp(j\varphi_1)+a_2\exp(j\varphi_2)\}\\ &AA^*=a_1^2+a_2^2+2~a_1a_2\cos(\varphi_2-\varphi_1)\end{aligned}\]

Elle sera maximale pour : \[\cos(\varphi_2-\varphi_1)=1\qquad\Rightarrow\qquad\Delta\varphi=\varphi_2-\varphi_1=2k\pi\]

C’est-à-dire que :

\[\begin{aligned} \frac{2\pi}{\lambda}~\big\{(d_2-d_1)+(r_2-r_1)\big\}&=2k\pi\\ (d_2-d_1)+(r_2-r_1)&=k\lambda\end{aligned}\]

Les distances \(d\) sont constante,s mais les distances \(r\) ne le sont pas : elles dépendent de \(x\), c’est-à-dire du point \(M\) du plan d’observation (écran).

On désigne par \(l\) la distance entre les deux sources secondaires et par \(D\) la distance du plan des sources à l’écran. Le calcul à effectuer s’appuie sur des considérations de géométrie et des approximations (infiniment petits) :

\[\begin{aligned} &r_2-r_1\approx S_2K=S_1S_2\sin\theta=l\sin\theta\approx\theta\\ &\frac{HM}{OH}=\frac{x}{D}=\tan\theta\approx\theta\\ &\delta=r_2-r_1\approx\frac{l~x}{D}\end{aligned}\]

Par suite, les points \(M\) où l’on observe le maximum d’intensité ont pour cote \(x\) telle que : \[\frac{l~x}{D}=k\lambda+(d_2-d_1) \qquad\Rightarrow\qquad x=\frac{k\lambda D}{l}+\frac{D}{l}(d_2-d_1)\]

Entre ces franges brillantes se situent les franges sombres, correspondant donc à un minimum d’intensité, c’est-à-dire : \[\cos(\varphi_2-\varphi_1)=-1\qquad\Rightarrow\qquad\Delta\varphi=(\varphi_2-\varphi_1)=(2k+1)\pi\]

On appelle interfrange la distance séparant deux franges de même nature, mesure faite de centre de frange à centre de frange : \[i = x_{k+1}-x_k=\frac{\lambda~D}{l}\]

Remarques

a) Les franges ne sont pas rigoureusement rectilignes car la relation : \[\delta=r_2-r_1\approx\frac{l~x}{D}\]

n’est qu’une approximation pour \(\theta\) petit. En fait, pour \(k\) donné, en écrivant que \(r_2-r_1=cte\), on voit que le lieu des points \(M\) est un hyperboloïde de révolution d’axe \(S_1S_2\).

Les franges sont en réalité des branches d’hyperboles assimilables à des segments de droite pour \(\theta\) très petit, donc pour \(HM = x\) petit.

b) En général, on prend la source primaire \(S\) sur l’axe du système, c’est-à-dire équidistante de \(S_1\) et \(S_2\), ce qui simplifie les équations avec \(d_2-d_1=0\).

c) Considérons maintenant le centre des interférences : \[k=0~:\quad\cos(\varphi_2-\varphi_1)=1\quad;\quad x=\frac{D}{l}(x_2-x_1)\]

On voit que la frange centrale est brillante et que cette frange et la source \(S\) sont situées de part et d’autre de l’axe du système. Il est évident que si \(S\) est située sur l’axe, la frange centrale sera elle aussi située sur l’axe, exactement au point \(H\).

1.2. Observation d’anneaux

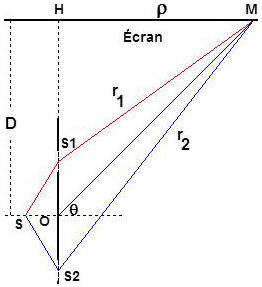Le plan d’observation est maintenant perpendiculaire à \(S_1S_2\). Son intersection avec les hyperboloïdes donnera donc des franges circulaires appelées anneaux.

Pour simplifier, nous supposerons \(d_1=d_2\). Cette fois, nous trouverons : \[r_2-r_1=l\cos(\theta)\]

Les anneaux seront brillants pour : \[r_2-r_1=k\lambda\]

En ayant recours aux approximations classiques : \[\cos\theta=\sqrt{1-\sin^2\theta}\approx\sqrt{1-\frac{\rho^2}{D^2}}\approx 1-\frac{\rho^2}{2D^2}\]

On aura donc : \[l\cos(\theta)=k\lambda\qquad\Rightarrow\qquad l~(l-\frac{\rho^2}{D^2})=k\lambda\] \[\rho^2=\frac{2D^2}{l^2}(l-k\lambda)\]

Le rayon de l’anneau d’ordre \(k\) a alors pour expression : \[\rho_k\approx D\sqrt{2}~\sqrt{1-\frac{k\lambda}{l}}\]

Remarque

Très souvent, on fait intervenir \(k_0\) appelé ordre d’interférence au centre. On l’obtient en faisant \(\theta=0\) : \[l\cos\theta=k\lambda\qquad\Rightarrow\qquad l=k_0\lambda\quad;\quad k_0=\frac{l}{\lambda}\]

Si cet ordre est un nombre entier, le premier anneau (central) est brillant. Si c’est un demi-entier alors cet anneau est sombre.

Noter que l’on peut écrire : \[\rho_k=D\sqrt{2}~\sqrt{1-\frac{k}{k_0}}\]

2. Emploi d’une fente source

Les franges engendrées par une source ponctuelle sont peu lumineuses. Pour augmenter leur éclat, on peut utiliser une fente source, mais sous certaines réserves. On sait que si l’on déplace la source primaire \(S\) suivant un mouvement de translation, le système de franges supposées rectilignes effectue un déplacement parallèle à celui de la source, mais de sens contraire. Par contre, si le déplacement de cette source s’effectue perpendiculairement au plan de la figure, il y a superposition des franges brillantes entre elles, car elles ne font que glisser sur elles-mêmes et il n’y a pas de brouillage.

Une source linéaire extrêmement fine, perpendiculaire au plan de la figure correspond à une infinité de positions de cette source \(S\) et le problème est matérialisé. Comme sources secondaires, on pourra alors prendre deux fentes fines parallèles à la première.

Il y a évidemment incohérence entre tous les points de \(S\), mais, pour chaque point, il y a cohérence entre les vibrations de \(S_1\) et de \(S_2\), de sorte que les systèmes de franges coïncident.

Influence de la largeur de la source linéaire

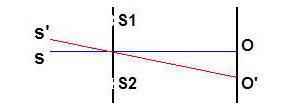Considérons deux sources ponctuelles \(S\) et \(S'\). Pour la première, la frange centrale est en \(O\) et pour la seconde en \(O'\). On sait que la valeur de l’interfrange reste la même :

• Superpositions de franges constructives : \(OO'=k~i\)

• Superpositions de frange destructives : \(OO'=k~i+\cfrac{i}{2}\)

Et il en est de même suivant les mêmes valeurs de \(SS'\). Ainsi, en écartant \(S\) et \(S'\), on voit apparaître et disparaître périodiquement le système de franges.

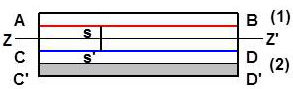Considérons à présent une source primaire qui soit une fente \(ABCD\) de largeur \(AD=i\). Partageons-la en deux parties égales par la médiane \(ZZ'\).

À tout point \(S\) de la partie (1) correspond un point \(S'\) de la partie (2) tel que \(SS'=i/2\). Leurs effets s’annulent comme nous venons de le voir et il y a alors extinction complète.

Si on élargit la fente, le système d’interfranges revient. Il est alors dû à la partie \(CDD'C'\) de la fente. Puis il disparaît pour une largeur \(2~i\) .

D’une façon générale, les franges disparaissent complètement chaque fois que la fente a une largeur \(e=k~i\). Ces disparitions successives sont séparées par des réapparitions de moins en moins visibles à mesure que l’éclairement uniforme augmente.

3. Dispositifs interférentiels

L’étude complète des dispositifs interférentiels ne présente pas ici d’intérêt particulier. Nous les rappelons pour mémoire, certains étant cependant étudiés :

– Trous de Young ou fentes de Young, précédemment étudiées

– Miroirs de Fresnel : La fente \(S\) est parallèle à l’arête de deux miroirs \(M_1\) et \(M_2\). Les sources secondaires sont les images respectives \(S_1\) et \(S_2\) de \(S\) par rapport à chacun des miroirs. Les interfranges s’observent dans la partie commune aux faisceaux issus de \(S_1\) et \(S_2\).

– Miroir de Lloyd : L’image \(S'\) interférant directement avec \(S\). Comme les ondes sont déphasées de \(\pi\) au moment de la réflexion, la frange centrale est noire.

– Bilentilles de Billet

– Biprisme de Fresnel

– Lames minces

– Interféromètres de Michelson, Jamin, Mach-Zender, Fabry-Perrot, etc.