1. Le rayonnement du corps noir. Formule de Planck
 Le rayonnement thermique est le rayonnement de lumière par des corps auxquels l’énergie est fournie exclusivement sous forme de chaleur.
Le rayonnement thermique est le rayonnement de lumière par des corps auxquels l’énergie est fournie exclusivement sous forme de chaleur.
Le corps noir est un corps idéal qui absorberait totalement toutes les radiations qu’il reçoit.
Ceci est réalisé en plaçant un corps dans une enceinte étanche au rayonnement et percée d’un petit trou ; le corps émet et absorbe continuellement du rayonnement et on aboutit à un état d’équilibre.
La densité d’énergie spectrale est donnée par la formule de Planck : \[u_{\lambda}=\frac{8\pi h~\nu^3}{c^3}\cdot\frac{1}{\exp(h\nu/kT)-1}\]
-
\(\nu\) : Fréquence du rayonnement
-
\(c\) : Vitesse de la lumière
-
\(h\) : Constante de Planck
-
\(k\) : Constante de Boltzman
-
\(T\) : Température absolue (en kelvins)
2. Émission et absorption de la lumière
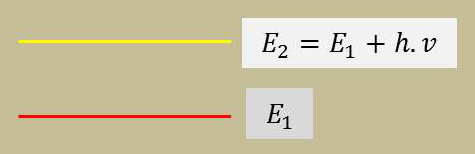 Pour simplifier, nous allons considérer un système à deux niveaux d’énergie \(N_1\) et \(N_2\), atomes dans les états respectifs \(E_1\) (état fondamental) et \(E_2\).
Pour simplifier, nous allons considérer un système à deux niveaux d’énergie \(N_1\) et \(N_2\), atomes dans les états respectifs \(E_1\) (état fondamental) et \(E_2\).
D’après la statistique de Boltzman : \[\frac{N_2}{N_1}=\exp\Big(-\frac{h~\nu}{k~T}\Big)\]
En envoyant de la lumière sur le système, on crée une densité d’énergie. Des atomes vont passer de l’état \(E_1\) à l’état \(E_2\) et le système sera excité.
\(B\) étant un coefficient de probabilité d’absorption, pendant un temps élémentaire \(dt\), le nombre \(N2\) s’accroît de : \[\delta N_2=B~u~N_1~dt\]
Pendant ce même temps, des atomes vont passer de l’état \(E_2\) à l’état \(E_1\) par émission spontanée. Ce nombre est évidemment proportionnel à \(N2\) : \[\delta'N_2=-A~N_2~dt\]
On est tenté de penser que les deux effets se compensent et on a alors : \[u=\frac{A}{B}~\exp\Big(-\frac{h~\nu}{k~T}\Big)\]
Ce résultat n’est compatible avec la formule de Planck que si l’on se place dans l’hypothèse où l’on écrit que: \[h~\nu\gg k~T\qquad\Rightarrow\qquad\frac{A}{B}=\frac{8\pi~h~\nu^3}{c^3}\]
Devant ce bilan incomplet, Einstein a été amené à considérer une autre émission dite émission induite (ou stimulée) : \[\delta''N_2=-B'~u~N_2~dt\]
Et Einstein postule l’égalité des probabilités de transitions \(E_1\leftrightarrow E_2\). On est ainsi conduit à la relation différentielle : \[\delta N_2+\delta'N_2+\delta''N_2=dN_2=0\]
Compte tenu de l’expression de \(A/B\), on retrouve exactement la formule de Planck.
3. Coefficient d’absorption
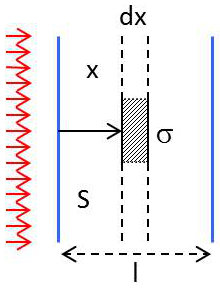 Soit un flux de photons de même vitesse et même direction contenus dans une section \(S\). Une molécule a pour section de capture \(\sigma\). Le photon a donc la probabilité \(\sigma/S\) d’être absorbé.
Soit un flux de photons de même vitesse et même direction contenus dans une section \(S\). Une molécule a pour section de capture \(\sigma\). Le photon a donc la probabilité \(\sigma/S\) d’être absorbé.
Supposons qu’il y ait \(N\) molécules par unité de volume et que \(\Phi\) soit le nombre de photons qui se présentent par unité de surface.
\(\Phi S\) photons ont la probabilité \(\sigma/S\) d’être absorbés par \(NS~dx\) molécules.
La probabilité pour un photon d’être absorbé par une molécule est : \[N~S~dx~\frac{\sigma}{S}=N~\sigma~dx\]
Il apparaitra \(\Phi~S~N~\sigma~dx\) photons donc \(d\Phi=-N~\Phi~\sigma~dx\) par unité de surface. \[\frac{d\Phi}{\Phi}=-N~\sigma~dx\qquad\Rightarrow\qquad\Phi=\Phi_0~\exp(-N~\sigma~x)\]
Le flux d’énergie est : \[c~[\varepsilon.E^2]=c~[\varepsilon~E_0^2]~\exp(-N~\sigma~x)\]
C’est-à-dire : \[E=E_0~\exp(-N~\sigma~x/2)\]
On sait que dans un milieu absorbant l’équation de propagation est : \[E=E_0\exp\big\{-j~\frac{2\pi}{\lambda}~(\nu-j\chi)~x\big\}\]
En identifiant, il vient : \[\frac{2\pi}{\lambda}=\frac{N~\sigma}{2}\]
Considérons le flux de photons traversant le milieu absorbant :
Des atomes en état [2] émettent un photon dans une direction quelconque (émission spontanée).
Il y a également émission induite ; le photon émis garde la même direction de propagation que le photon incident.
Dans le faisceau sortant, il y aura un photon de plus et la lumière induite émise est cohérente avec la lumière incidente.
On a alors, avec \(\sigma_{21}\) : section efficace pour l’émission induite : \[\frac{d\Phi}{\Phi}=-N_1~\sigma_{12}~dx+N_2~\sigma_{21}~dx\]
On a alors : \[|E|=|E_0|~\exp[(N_2~\sigma_{21}-N_1~\sigma_{12})~\frac{x}{2}]\]
Et compte tenu de l’équation de propagation : \[\frac{2\pi}{\lambda}~\chi=\frac{N_1}{2}-\frac{N_2}{2}~\sigma_{21}\]
4. Masers optiques ou lasers
La signification du sigle laser est : Light Amplification by Stimulated Emission of Radiation. Cette amplification est réalisée lorsque \(\chi<0\), ce qui entraine \(N_2>N_1\).
On y parvient par plusieurs moyens :
-
Le pompage optique
On réalise un faisceau de lumière intense : il y a alors un grand nombre de molécules excitées, le niveau [2] devenant plus « habité » que le niveau [1]. On a alors \(\chi<0\), mais ceci ne dure qu’un très court instant.
-
Le phénomène de plasma
Les décharges électriques dans les gaz donnent un milieu actif. Par ce procédé, on peut obtenir \(\chi<0\) aussi longtemps que l’on veut.
4.1. Interféromètre de Fabry–Perrot
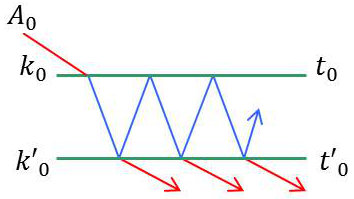 On se place dans les conditions de l’incidence normale, c’est-à-dire : \(\delta=2n~e\)
On se place dans les conditions de l’incidence normale, c’est-à-dire : \(\delta=2n~e\)
Rappelons l’expression de l’indice complexe : \(n=\nu-j\chi\)
Amplitude de la première onde transmise : \[A_0~t_0~\exp\big(-j~2\pi~\frac{n~e}{\lambda}\big)~t'_0\]
Amplitude de la deuxième onde transmise (après deux réflexions) \[A_0~t_0\exp\big(-j~2\pi~\frac{n~e}{\lambda}\big)~k'_0~k_0~\exp\big(-j~2\pi~\frac{n~e}{\lambda}\big)~t'_0\]
Amplitude de la nième onde transmise (après réflexions multiples) \[A_0~t_0\exp\big(-j~2\pi~\frac{n~e}{\lambda}\big)~\{~~\}^{n-1}~t'_0\]
Et en utilisant la relation : \[1+q+q^2+\dots+q^n=\frac{1}{1-q}\]
L’expression de l’amplitude totale devient : : \[A=A_0~t_0~t'0~\exp\big(-j~2\pi~\frac{n~e}{\lambda}\big)~\frac{1}{1-k_0~k'_0~\exp(-j~4\pi~n~e~/\lambda)}\]
Or, on a posé : \(n=\nu-j\chi\). Il vient donc : \[A=\frac{A_0~t_0~t'_0~\exp(-j~2\pi~\nu~e/\lambda)~\exp(-2\pi~\chi~e/\lambda)}{1-k_0~k'_0~\exp(-j~4\pi~\nu~e/\lambda)~\exp(-4\pi~\chi~e/\lambda)}\]
On pose :
\[\begin{aligned} |t_0~t'_0|=T_0\quad&;\quad|k_0~k'_0|=K_0\\ \varphi=\frac{4\pi~\nu~e}{\lambda}\quad&;\quad k=\frac{4\pi~\chi}{\lambda}\end{aligned}\]
Le coefficient de transmission en énergie est donc :
\[\begin{aligned} T&=\frac{AA^*}{A_0A_0^*} \\ T&=\frac{T_0^2}{(1-K_0~e^{-j\varphi}~e^{-ke})~(1-K_0~e^{+j\varphi}~e^{-ke})} \\ T&=\frac{T_0^2}{(1-K_0~e^{-ke})^2+4~K_0~\sin^2(\varphi/2)}\end{aligned}\]
Supposons pour simplifier que \(K_0\in \mathbb R\), que \(K_0<1\) et que le Fabry-Perrot soit accordé, c’est-à-dire que \(\varphi=m~\pi\). On a alors : \[T=\frac{T_0^2}{(1-K_0~e^{-ke})^2}\]
Comme \(e^{-ke}<1\), on voit que \(T>1\) avec \(k=\dfrac{4\pi~\chi}{\lambda}\).
Donc, si \(k\) augmente, il arrivera que \(e^{-ke}=\dfrac{1}{K_0}\), c’est’à-dire que \(T\rightarrow\infty\).
L’effet laser est ainsi la réalisation de deux phénomènes :
-
le laser est une source de lumière cohérente ;
-
l’onde est focalisable en un point où l’on peut trouver toute l’énergie produite dans un volume aussi grand que l’on voudra.
