1. Avertissement

Un tel chapitre devrait être normalement présenté en deux grandes parties : celle correspondants aux filtres électriques et celle correspondant aux filtres mécaniques. D’autant qu’il y a de nombreuses analogies d’une technologie à l’autre.

Nous ne traiterons cependant que de la deuxième, les filtres mécaniques, les filtres électriques étant classés dans la catégorie électricité-électronique (voir pour cela la rubrique Réseaux linéaires.

2. Filtres mécaniques. Généralités

Comme en électricité on peut rencontrer en mécanique :

1. des filtres passe-bas ne laissant passer que les pulsations \(\omega\) telles que \(\omega<\omega_1\) ;

2. des filtres passe-bande ne laissant passer que les pulsations \(\omega\) telles que \(\omega_1<\omega<\omega_2\) ;

3. des filtres passe-haut ne laissant passer que les pulsations \(\omega\) telles que \(\omega>\omega_2\).

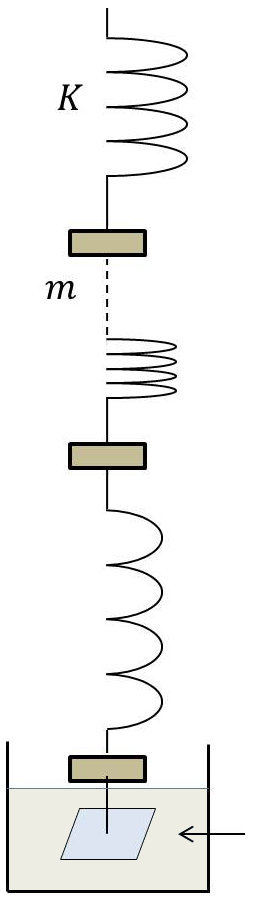
Considérons l’exemple ci-contre dans lequel la force oscillante est verticale et dans lequel un frottement visqueux est imposé par la palette. Il est clair que les oscillations lentes passeront facilement ; par contre les oscillations rapides ne passeront pas.

Dans ce qui suit, nous étudierons en détail le cas d’un filtre passe-bande, les deux autres cas pouvant s’étudier d’une façon encore plus simple.

On rappelle les propositions suivantes (analogies mécanique – électricité) : \[m\leftrightarrow L\quad;\quad k\leftrightarrow\frac{1}{C}\quad;\quad f\leftrightarrow R\]

Pour deux ressorts en série, équivalence ressort unique : \[\text{Raideur :}\qquad \frac{1}{k}=\frac{1}{k_1}+\frac{1}{k_2}\]

Pour deux ressorts en parallèle, équivalence ressort unique : \[k=k_1+k_2\]

Résultats qui se généralise au cas de plusieurs ressorts.

3. Constitution d’un filtre mécanique passe-bande

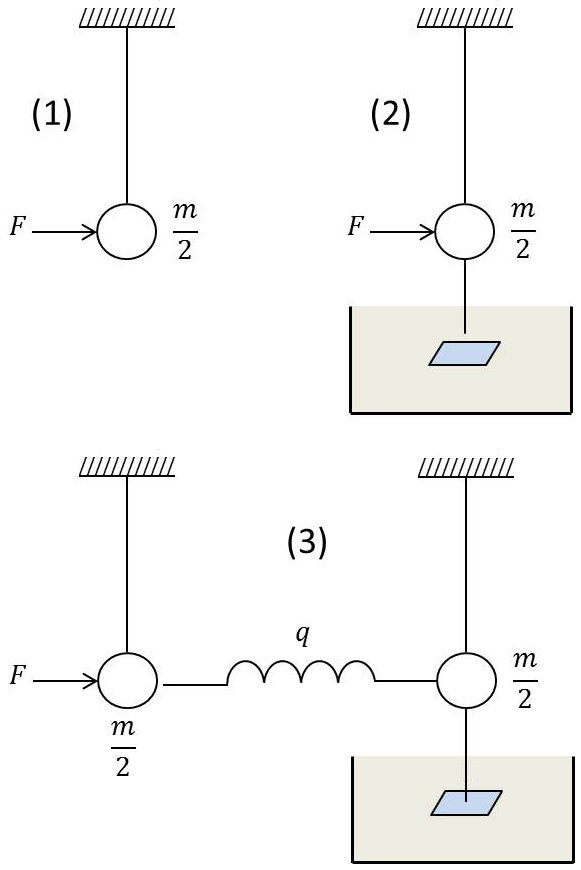1) Considérons le pendule (1) de longueur de fil très grande \(l\) et de masse \(m/2\) attaqué par une force oscillante \(F\). Son impédance, que nous désignerons par \(s/2\), est donnée par : \[\frac{s}{2}=\frac{j~m~\omega}{2}+\frac{k}{2~j~\omega}\quad;\quad k=\frac{m~g}{l}\]

La notation \(s/2\) est une notation consacrée pour une branche série de filtre électrique en échelle (cellules symétriques).

2) Considérons maintenant le pendule (2) identique mais amorti par le frottement visqueux \(f\). Son impédance est : \[\frac{s}{2}+f\]

3) Couplons ces deux pendules par un ressort de raideur \(q\) (impédance du ressort isolé : \(d=q/j~\omega\)) pour former le système couplé.

L’impédance du primaire non couplé est : \[\frac{s}{2}+d\]

Celle du secondaire non couplé est : \[\frac{s}{2}+d +f\]

L’impédance d’entrée \(Z\) du système est donc : \[Z=\frac{s}{2}+d+\frac{q^2}{\omega^2~\Big(\cfrac{s}{2}+d+f\Big)}=\frac{s}{2}+d-\frac{d^2}{\cfrac{s}{2}+d+f}\]

Cherchons à régler \(f\) de telle sorte que \(Z\) se réduise à la résistance visqueuse \(f\).

Il faut : \[\frac{s}{2}+d-f=\frac{d^2}{\cfrac{s}{2}+d+f}\quad\Rightarrow\quad f^2=s~d+\frac{s^2}{4}=f_0^2\]

Pour pouvoir faire l’expérience, il faut que \(f_0\) existe, c’est-à-dire : \[s~d+\frac{s^2}{4}>0\]

En remplaçant s et d par leurs expressions, on trouve que l’on doit avoir :

\[\begin{aligned} &\omega_1<\omega<\omega_2\\ &\omega_1=\sqrt{\frac{k}{m}}=\sqrt{\frac{k/2}{m/2}}\quad;\quad \omega_2=\sqrt{\frac{k+4~q}{m}}=\sqrt{\frac{(k/2)+2~q}{m/2}}\end{aligned}\]

Ce sont précisément les pulsations principales du système couplé constitué par les deux pendules \(m/2\) sans amortissement.

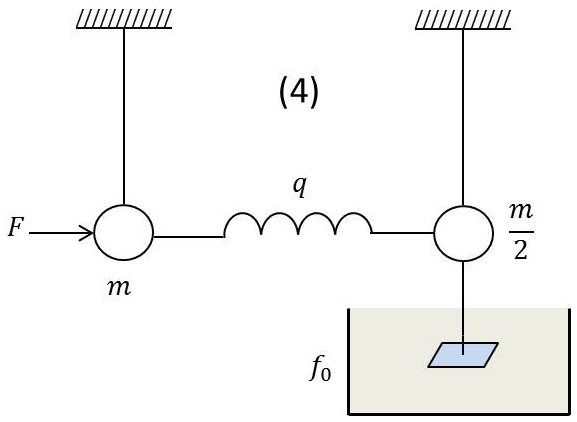Supposons donc \(\omega\) compris dans ces limites et réglons \(f=f_0\).

Remarquons alors que le système couplé ci-contre (4) a une impédance d’entrée \[\frac{s}{2}+f_0\]

et donc équivalent au pendule (2).

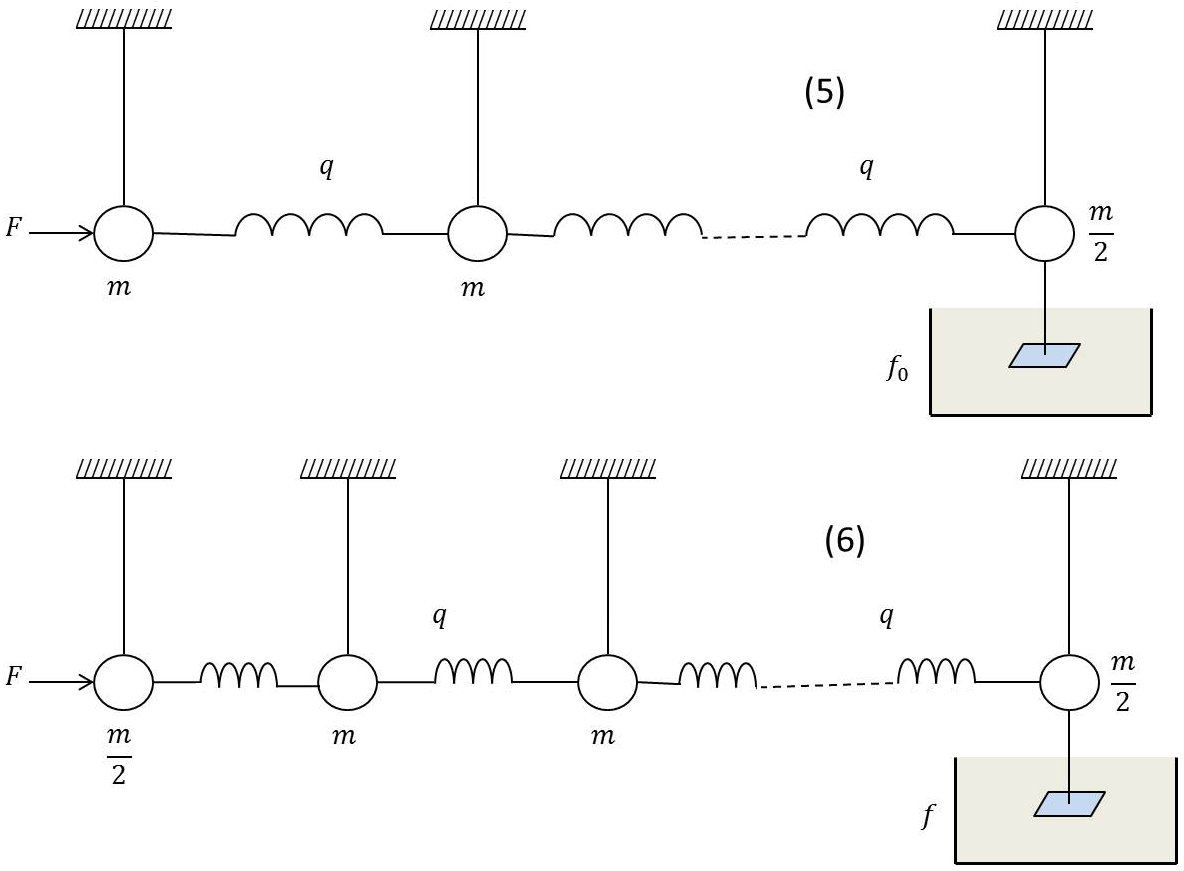Il en est de même du système (5) formé d’un grand nombre de pendules, comme on le verrait immédiatement par récurrence.

Formons alors le système (6) en couplant à (5), en avant, un pendule de masse \(m/2\). Il est équivalent (on le voit par récurrence) au système (3) et il a par suite a une impédance d’entrée \(f_0\).

Attaquons (6) par la force oscillante \(F\) :

Le pendule (1) prend une vitesse en phase avec \(F\) (puisque l’impédance d’entrée est réelle et positive). Le pendule (2) prend le même mouvement que celui du secondaire du système (3) lorsqu’on applique la force \(F\) à ce système.

Or, dans le système (3), le secondaire prend un mouvement de même amplitude que le primaire (puisque la dissipation d’énergie sur \(f_0\) doit être la même que si \(F\) était directement appliquée à \(f_0\) seule) et simplement déphasé par rapport au mouvement du primaire d’un certain angle \(\alpha\). Il en est donc de même du pendule 2 du système (6).

Quant au pendule 3, il est soumis à la même action de ressort sur sa gauche que le pendule 2 et il présente la même impédance d’entrée. Il prendra donc le même mouvement, avec un déphasage sur le pendule 2, et par suite sur la force \(F\), et ainsi de suite ; les pendules prennent des mouvements de même amplitude et dont les phases varient en progression arithmétique.

Le système (6) a donc les caractéristiques d’un filtre. C’est un filtre passe-bande, car l’existence de \(f_0\) exige que \(\omega\) soit compris entre les pulsations de coupure (\(\omega_1,~\omega_2\)).

Retrouvons ces résultats par une théorie calquée sur celle des filtres électriques :

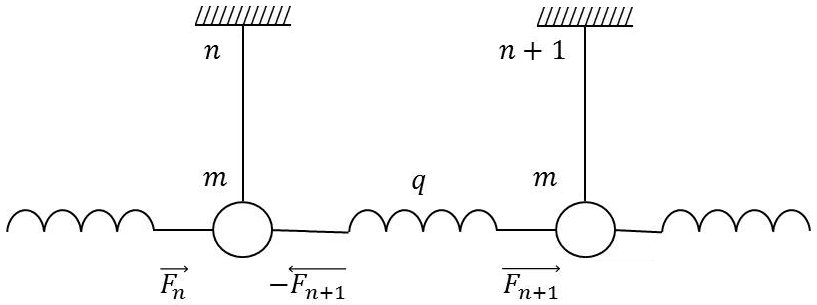Soient \([X_n,~V_n]\), en régime permanent, les amplitudes complexes de l’élongation et de la vitesse du pendule \(n\) (de masse \(m\)) et \([X_{n+1},~V_{n+1}]\) celles du pendule \(n+1\).

Ces pendules sont soumis, respectivement, de la part des ressorts situés à leur gauche, à des forces d’amplitudes complexes \([F_n,~F_{n+1}]\).

L’impédance constituée par le pendule \(n\) et tout ce qui est à droite est \((s/2)+f\). Il en est de même de l’impédance constituée par le pendule \(n+1\) et tout ce qui est à droite.

On a donc : \[\begin{aligned} &F_n=\Big(\frac{s}{2}+f\Big)~V_n\\ &F_{n+1}=\Big(\frac{s}{2}+f\Big)~V_{n+1}\\ \end{aligned} \quad\Rightarrow \qquad\frac{F_{n+1}}{F_n}=\frac{V_{n+1}}{V_n}\]

Le ressort \(q\) dessiné sur la figure exerce à sa gauche sur le pendule \(n\) la force [\(-F_{n+1}\)]. Ce pendule \(n\) de masse \(m\) et par suite d’impédance \(s\) est donc soumis à la force totale [\(F_n-F_{n+1}\)].

On a donc : \[F_n-F_{n+1}=s~V_n\]

Enfin, la tension du ressort \(q\) est fournie par la compression [\(X_n-X_{n+1}\)].

On a donc : \[F_{n+1}=q~(X_n-X_{n+1})=\frac{q}{j~\omega}~(V_n-V_{n+1})=d~(V_n-V_{n+1})\]

On en tire : \[\frac{F_{n+1}-F_n}{F_{n+1}}=\frac{V_{n+1}-V_n}{V_{n+1}}=\frac{-s~V_n}{-d~(V_{n+1}-V_n)}\]

Et, tous calculs faits : \[\Big(\frac{V_{n+1}}{V_n}\Big)^2-2~\Big(1+\frac{s}{2~d}\Big)~\frac{V_{n+1}}{V_n}+1=0\]

Équation identique à celle obtenue pour les filtres électriques et que l’on pourrait traiter de la même façon.

Remarque

Dans tout ce qui précède, qu’il s’agisse de filtres électriques ou filtres mécaniques, nous avons établi que l’équation de récurrence liant les amplitudes d’oscillation dans deux cellules successives en partant d’une équation initiale qui exprime l’impédance vue à droite par un élément quelconque du filtre est toujours la même, quel que soit le numéro d’ordre de cet élément.

Or, nous avons obtenu cette équation en admettant que le filtre est fermé sur son impédance caractéristique. On peut se demander quelle est a valeur de ces calculs lorsque le filtre est fermé sur une impédance quelconque. Il semble à première vue que l’on puisse aisément lever la difficulté en se plaçant dans le cas d’un filtre infiniment long, c’est-à-dire comprenant un nombre infiniment grand de cellules.

Il suffit alors de remarquer que quelle que soit la cellule que l’on considère, elle est toujours suivie vers la droite par un nombre de cellules infiniment grand et voit toujours vers la droite la même impédance, quelle que soit la valeur de l’impédance terminale qui se trouve infiniment éloignée.

Toutefois, il ne faut pas oublier qu’en raisonnant sur des impédances, nous supposons essentiellement que nous nous trouvons en régime permanent et que nous avons donc attendu assez longtemps pour que toutes les cellules du filtre aient été intéressées par l’oscillation. On ne pourra donc lever la difficulté que par un raisonnement ne faisant pas entrer en ligne de compte la notion d’impédance et qui sera valable aussi bien pour le régime transitoire que pour le régime permanent.

Relation de récurrence

Reprenons alors le problème du filtre mécanique que nous venons d’étudier et essayons d’obtenir directement une relation de récurrence entre les mouvements des pendules successifs, sans faire intervenir le fait que le filtre est fermé à l’extrémité sur une impédance particulière.

Dans ce but, considérons le filtre mécanique formé par une succession indéfinie de pendules de masse \(m\), tous identiques, rappelés vers le repos par des forces et soumis à l’action des pendules voisins.

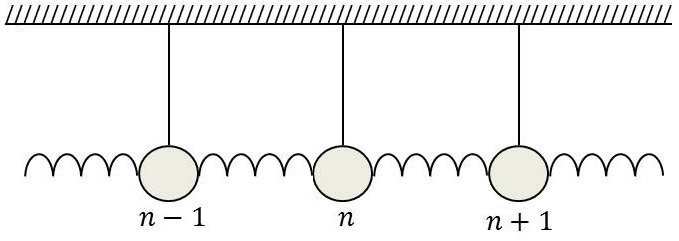Nous écrirons que la force totale qui s’exerce sur la masse \(n\) comprend :

• la force de rappel \(-k~x_n\) ;

• la force \(q~(x_{n+1}-x_n)\) exercée par le ressort de droite ;

• la force \(q~(x_{n-1}-x_n)\) exercée par le ressort de gauche.

Nous obtenons l’équation différentielle : \[m~\frac{d^2x_n}{dt^2}+(k+2~q)~x_n-q~(x_{n+1}+x_{n-1})=0\]

Cherchons une solution de cette équation qui puisse se représenter par un ensemble de mouvements de pulsation \(\omega\), de même amplitude, et dont les phases varient en progression arithmétique, soit, en notation complexe : \[x_n=a~\exp~j(\omega~t-n~\alpha)\]

La substitution conduit à : \[-m~\omega^2+(k+2~q)-q~\{\exp(j~\alpha)+\exp(-j~\alpha)\}\]

Soit encore: \[\cos\alpha=1+\frac{k-m~\omega^2}{2~q}=1+\frac{s}{2~d}\]

\(s\) et \(d\) désignant les mêmes quantités que pour le calcul précédent.

Nous retrouvons donc la condition \(-1~\leq~\frac{s}{4~d}~\leq~0\) de la bande passante (voir les filtres électriques), condition nécessaire pour que la solution soit acceptable et qui se traduit par la condition : \[\sqrt{\frac{k}{m}}~\leq~\omega~\leq~\sqrt{\frac{k+2~q}{m}}\]

Les deux pulsations limites correspondent à un déphasage nul ou égal à \(\pi\) entre deux pendules successifs.

Pour une telle valeur de \(\omega\), la file illimitée de pendules peut être le siège de deux ondes sinusoïdales se propageant en sens inverse et pour lesquelles le déphasage \(\alpha\) entre le pendule \(n\) et le pendule \(n+1\) est égal, soit à \(\alpha\), soit à \(-\alpha\), \(\alpha\) étant donné par l’équation obtenue plus haut : \[\cos\alpha=1+\frac{k-m~\omega^2}{2~q}\]

Le mouvement le plus général de pulsation est alors obtenu par superposition de ces deux ondes et s’écrit : \[x_n=a~\exp~j~(\omega~t-n~\alpha)+b~\exp~j~(\omega~t+n~\alpha)\]

La pulsation \(\omega\) et les amplitudes complexes \(a\) et \(b\) peuvent être choisies de façon que le mouvement satisfasse à n’importe quel type de conditions imposées à deux pendules déterminés.

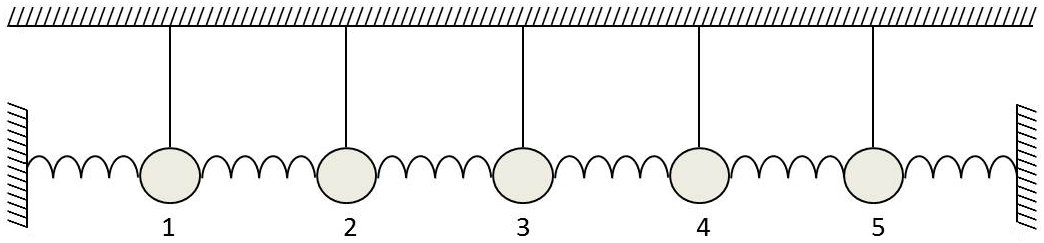On peut par exemple supposer que l’on immobilise de façon permanente les modules de numéro \(1\) et \(p+1\), ce qui revient à étudier le mouvement d’une file de p pendules fixés par des ressorts de raideur \(q\) à des armatures rigides (dans le cas de la figure : p = 5), ce qui conduit aux limites : \[a~\exp(-j~n~\alpha)+b~\exp(j~n~\alpha)=0\qquad\text{pour :}\quad n=0~;~n=p\]

Soit : \[a+b=0\quad\text{et}\quad\sin p~\alpha=0\qquad\text{donc :}\quad\alpha=\frac{K~\pi}{p}\quad (K~\text{entier})\]

On trouve ainsi \(p\) mouvements principaux distincts en faisant successivement \(K=1,~2,~\dots,~p\). Le mouvement général est obtenu par superposition de ces \(p\) mouvements principaux.

On pourrait poursuivre en introduisant la notion de vitesse de propagation \(\omega\).

Nous n’insisterons pas sur ce sujet et passerons directement à l’étude des systèmes linéaires, comportant une infinité de degrés de liberté, où se présente une situation tout à fait analogue à ceci près que la vitesse de propagation de la phase est indépendante de la fréquence.

Il en résulte que le système linéaire est capable de transporter sans déformation un signal de forme quelconque, puisqu’il transporte à la même vitesse toutes les composantes de sa décomposition en intégrale de Fourier.