1. Mouvement dans un champ central symétrique

En mécanique quantique, le problème du mouvement de deux particules en interaction peut être réduit à celui d’une seule particule.

Considérons deux particules de masses respectives \(m_1,~m_2\), interagissant suivant la loi \(U\) (potentiel). Le hamiltonien du système peut être partitionné : \[\widehat{H}~=~-\frac{\hbar^2}{2-m_1}~\Delta_1~-~\frac{\hbar^2}{2-m_2}~\Delta_2~+~U\qquad(1)\]

Introduisons deux nouvelles coordonnées \[r~=~r_2-r_1\quad;\quad R~=~\frac{m_1-r_1+m_2-r_2}{m_1+m_2}\qquad(2)\]

• \(r\) : distance entre les particules

• \(R\) : rayon vecteur du centre d’inertie des particules

\[\widehat{H}~=~-\frac{\hbar^2}{2~(m_1+m_2)}~\Delta_R~-~\frac{\hbar^2}{2~m}~\Delta_r~+~U(r)\qquad(3)\]

• \(m_1+m_2\) : masse totale du système

• \(m~=~\cfrac{m_1~m_2}{m_1+m_2}\) : masse réduite du système

Le hamiltonien étant décomposé en deux parties indépendantes, on posera à priori : \[\Psi(r_1,~r_2)~=~\varphi(R)~\psi(r)\]

• \(\varphi(R)\) : mouvement libre du centre d’inertie (masse \(m_1+m_2\))

• \(\psi(r)\) : mouvement relatif des particules (masse \(m\) dans \(U=U(r)\))

L’équation de Schrödinger d’une particule a pour expression : \[\Delta\Psi~+~\frac{2~m}{\hbar^2}~\{E-U(r)\}~\Psi~=~0\qquad(4)\]

Introduisant l’expression du laplacien \(\Delta\Psi\) en coordonnées sphériques : \[\begin{aligned} \frac{1}{r^2}~\frac{\partial}{\partial r}\Big(r^2~\frac{\partial\Psi}{\partial r}\Big) ~+~&\frac{1}{r^2}~\Big\{\frac{1}{\sin\theta}~\frac{\partial}{\partial\theta}\Big(\sin\theta~\frac{\partial\Psi}{\partial\theta}\Big) ~+~\frac{1}{\sin^2\theta}\frac{\partial^2\Psi}{\partial\varphi^2}\Big\} \\ ~+~&\frac{2~m}{\hbar^2}~\Big\{E-U(r)\Big\}~\Psi=0 \end{aligned}\qquad(5)\]

Introduisant l’opérateur du carré du moment de la particule : \[\widehat{\vec{l}}^2~=~-\Big\{\frac{1}{\sin^2\theta}~\frac{\partial^2}{\partial\varphi^2} ~+~\frac{1}{\sin\theta}~\frac{\partial}{\partial\theta}\Big(\sin\theta~\frac{\partial}{\partial\theta}\Big)\Big\}\]

On peut donc écrire : \[\frac{\hbar^2}{2~m}~\Big\{-\frac{1}{r^2}~\frac{\partial}{\partial r}\Big(r^2~\frac{\partial\Psi}{\partial r}\Big) ~+~\frac{\widehat{l}^2}{r^2}~\Psi\Big\}~+~U(r)~\Psi~=~E~\Psi\qquad(6)\]

Nous chercherons des solutions sous la forme d’un produit : \[\Psi~=~R(r)~Y_{lm}(\theta,~\varphi)\qquad(7)\]

Comme on doit avoir : \[\widehat{l}^2~Y_{lm}~=~l~(l+1)~Y_{lm}\]

On obtient pour la fonction radiale \(R(r)\) l’équation : \[\frac{1}{r^2}~\frac{\partial}{\partial r}\Big(r^2~\frac{dR}{dr}\Big) ~-~\frac{l~(l+1)}{r^2}~R~+\frac{2~m}{\hbar^2}~\{E-U(r)\}~R~=~0\qquad(8)\]

En effectuant la substitution : \[R(r)~=~\frac{\chi(r)}{r}\qquad(9)\]

l’équation (8) se ramène à la forme : \[\frac{d^2\chi}{dr^2}~+~\Big\{\frac{2~m}{\hbar^2}~(E-U)~-~\frac{l~(l+1)}{r^2}\Big\}~\chi~=~0\qquad(10)\]

Si \(U(r)\) est partout finie, il en sera de même de \(\Psi\) et donc de sa partie réelle \(R(r)\).

\(\chi(r)\) doit donc s’annuler pour \(r=0\) : \[\chi(0)~=~0\qquad(11)\]

Cette condition se conserve en fait pour un champ devenant infini lorsque \(r~\rightarrow~\infty\).

La condition de normalisation se conserve pour les deux fonctions : \[\int_0^{+\infty}|R|^2~r^2~dr\qquad;\qquad \int_0^{+\infty}|\chi|^2~dr\]

L’équation (10) coïncide formellement avec l’équation de Schrödinger pour un mouvement à une dimension dans un champ d’énergie potentielle : \[U_l(r)~=~U(r)~+~\frac{\hbar^2}{2~m}~\frac{l~(l+1)}{r^2}\qquad(12)\]

\(U_l(r)\) est souvent appelé potentiel effectif.

Dans un champ central symétrique, le mouvement revient à celui d’un mouvement à une dimension dans une région limitée d’un côté (condition à la limite pour \(r=0\)).

Dans un tel mouvement les niveaux d’énergie sont non dégénérés. La donnée de l’énergie détermine donc complètement la solution de l’équation (10), c’est-à-dire la partie radiale de la fonction d’onde.

La partie angulaire de la fonction d’onde étant complètement déterminée par les valeurs de (\(l,~m\)), nous en concluons que, lors du mouvement dans un champ central symétrique, la fonction d’onde est complètement déterminée par les valeurs de {\(E,~l,~m\)}.

Énergie, carré du moment et composante sur l’axe des \(z\) du moment forment un ensemble complet de grandeurs physiques pour caractériser un tel mouvement.

Symbolisme adopté pour désigner les états correspondant à différentes valeurs de \(l\) : \[\begin{matrix} &l=&0&1&2&3&4&5\\ & &s&p&d&f&g&h \end{matrix}\]

L’état normal pour le mouvement d’une particule est toujours l’état \(s\).

En effet, pour \(l\neq0\), la partie angulaire de la fonction d’onde a toujours des nœuds alors que la fonction d’onde de l’état normal ne doit nullement en avoir.

Pour \(l\) donné, la plus petite valeur propre possible de l’énergie croît avec \(l\). Ceci résulte déjà du fait que la présence du moment se traduit par l’adjonction à l’hamiltonien du terme essentiellement positif (relation 12) : \[\frac{\hbar^2~l~(l+1)}{2~m~r^2}\qquad(\text{croissant avec } l)\]

Allure de la fonction radiale au voisinage de l’origine des coordonnées. Hypothèse : \[lim_{~r~\rightarrow~0}~U(r)~r^2~=~0\]

Solution retenue : au voisinage de l’origine les fonctions d’onde des états correspondants à \(l\) donné sont proportionnelles à \(r^l\) : \[R_l~\approx~\text{cte}~r^l\]

La probabilité qu’une particule se trouve à la distance du centre comprise entre \(r\) et (\(r+dr\)) est déterminée par : \[r^2~|R|^2\qquad\text{donc proportionnelle à :}\quad r^{2(l+1)}\]

On voit qu’elle s’annule d’autant plus vite à l’origine que \(l\) est grand.

2. Mouvement dans un champ coulombien

Un cas extrêmement important est celui du champ coulombien : \[U~=~\pm~\frac{\alpha}{r}\qquad\alpha>0 \text{, constante}\]

Nous envisagerons d’abord le cas de l’attraction : \[U~=~-~\frac{\alpha}{r}\]

2.1. Équation des fonctions radiales

Il résulte de considérations générales que :

• le spectre des valeurs propres négatives de l’énergie estdiscret (infinité de niveaux) ;

• le spectre des énergies positives est continu.

L’équation (8) des fonctions radiales s’écrit : \[\frac{d^2R}{dr^2}~+~\frac{2}{r}~\frac{dR}{dr}-~~\frac{l~(l+1)}{r^2}~R ~+~\frac{2~m}{\hbar^2}~\Big(E+\frac{\alpha}{r}\Big)~R~=~0\qquad(13)\]

Dans le cas du mouvement relatif de deux particules attractives, \(m\) est la masse réduite.

2.2. Ordres de grandeur

\(m~=~9,11\times 10^{-28}~\rm g\)

\(\alpha~=~e^2\qquad\) (\(e\) : charge de l’électron)

Unité atomique de longueur : \[(1~{\rm ua})_l~=~\frac{\hbar^2}{m~e^2}~=~0,529\times 10^{-8}~\rm cm\quad(\text{rayon de Bohr})\]

Unité d’énergie atomique : \[(1~{\rm ua})_e~=~\frac{m~e^4}{\hbar^2}~=~27,21~\rm eV\]

2.3. Représentation du potentiel

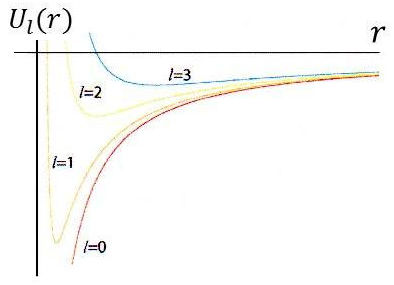La figure ci-contre représente un exemple de potentiels effectifs en \(\alpha/r\).

Elle correspond à une énergie électrostatique pour \(\alpha=1\) et \(l=0,~1,~2,~3\).

Tous ces potentiels forment un puits, mais celui-ci est d’autant moins profond que \(l\) est grand.

Le potentiel effectif a un minimum en : \[r_{min}~=~\frac{l~(l+1)~\hbar^2}{m~\alpha}\]

3. États liés et états libres

Le potentiel de l’exemple montre qu’il n’existe de puits que pour des particules dont l’énergie est \(E<E_q\) (valeur donnée).

Une particule telle que \(E>Eq\) sera libre, car la probabilité de la trouver loin de la position {\(r = 0\)} est non nulle.

Au contraire, une particule d’énergie inférieure à \(Eq\) restera confinée au voisinage du fond de puits de potentiel.

• Les niveaux d’énergie \(E>Eq\) correspondent à des états libres : les énergies ne seront pas quantifiées.

• Les niveaux d’énergie \(E<Eq\) correspondent à des états liés : les énergies seront quantifiées.

Seuls sont intéressants les états liés.

Remarques

1. Passer d’un état lié à un état libre correspond à l’ionisation de l’atome.

2. Plus \(l\) est grand, plus les niveaux d’énergie sont proches du seuil d’ionisation.