1. Système à deux particules

Raisonnons comme s’il s’agissait d’un couple de particules quelconques :

• de masses respectives \(m_1\) et \(m_2\) ;

• de coordonnées respectives \(r_1\) et \(r_2\) ;

• en interaction mutuelle \(U(r_1-r_2)\).

Ce potentiel ne dépend que de la position relative des deux particules.

Le système est également décrit par ses fonctions d’onde \(\Psi(r_1,~r_2)\).

Le hamiltonien a pour expression (\(\widehat{p}_i\) : opérateur impulsion d’une particule \(i\)) : \[\widehat{H}~=~\frac{\widehat{p}_1^2}{2~m_1}~+~\frac{\widehat{p}_2^2}{~2m_2}~+~U(\widehat{r}_1-\widehat{r}_2)\qquad(1)\]

Position et impulsion du centre de masse : \[\overrightarrow{R}~=~\frac{m_1~\overrightarrow{r_1}+m_2~\overrightarrow{r_2}}{m_1+m_2}\qquad;\qquad\overrightarrow{P}~=~\overrightarrow{p_1}+\overrightarrow{p_2}\qquad(2)\]

Position et impulsion relatives : \[\widehat{r}~=~\widehat{r}_1-\widehat{r}_2\qquad;\qquad\widehat{p}~=~\frac{m_2~\widehat{p}_1-m_1~\widehat{p}_2}{m_1+m_2}\qquad(3)\]

Expression développée du hamiltonien : \[\widehat{H}~=~\widehat{H}_{cm}~+~\widehat{H}_{rel}\qquad(4)\]

Avec :

\[\begin{aligned} \widehat{H}_{cm}~&=~\frac{\widehat{P}^2}{2~M} &&M~=~m_1+m_2\quad(\text{masse totale}) &&(5)\\ \widehat{H}_{rel}~&=~\frac{\widehat{p}^2}{2~\mu}+U(\overrightarrow{r}) &&\mu~=~\frac{m_1m_2}{m_1+m_2}\quad(\text{masse réduite}) &&(6)\end{aligned}\]

(5) caractérise le mouvement libre du centre de masse du système.

(6) caractérise le mouvement relatif des particules (interaction ou potentiel).

2. Atome d’hydrogène (électron + proton)

2.1. Équation radiale

Deux hypothèses simplificatrices :

1. effets dus au spin de l’électron négligés ;

2. masse du proton \(m_p\) infiniment lourde par rapport à \(m_e\), celle de l’électron.

Champ coulombien pour l’électron (charge élémentaire \(q\)) : \[U(r)=-\frac{e^2}{r}\qquad;\qquad e^2=\frac{q^2}{4\pi~\varepsilon_0}\]

Équation radiale : \[\Big(-\frac{e^2}{r}~\frac{d^2}{dr^2}r+\frac{l~(l+1)}{2~m_e~r^2}-\frac{e^2}{r}~\Big)~R_l(r)~=~E~R(r)\qquad(7)\]

2.2. Équation radiale sans dimension

Introduisons les quantités (sans dimension) : \[\rho=\frac{r}{a_0}\quad\text{et}\quad\varepsilon=-\frac{E}{E_1}\qquad;\qquad(a_0=0,53~\rm\text{Å}=53~pm)\]

Nous obtenons l’équation sans dimension : \[\Big(\frac{1}{\rho}~\frac{d^2}{dr^2}~\rho~-~\frac{l~(l+1)}{\rho^2}~+~\frac{2}{\rho}~-~\varepsilon\Big)~R_l(\rho)~=~0\]

1) Pour chaque valeur de \(l\), nous obtenons un nombre infini de relations normalisables :

\[\begin{aligned} R_l~&=~\exp(-\sqrt{\varepsilon})~\rho^l~\mathcal{L}_{n',l}~(\rho)\quad;\quad n'=0,~1,~\dots\\ \mathcal{L}_{n',l}~(\rho)~&=~L_0~+~L_1~\rho~+~....~+~L_{n'}~\rho^{n'}\end{aligned}\]

• \(\mathcal{L}\) : polynôme de Laguerre de degré \(n'\) (\(n'\) zéros réels entre \(p=0\) et \(p=+\infty\))

• \(n'\) : nombre de noeuds de la fonction d’onde radiale (nombre quantique radial).

• \(n=n'+n+l\) : nombre quantique principal

Chaque solution de l’équation de Schrödinger en coordonnées sphériques correspond à un état lié du problème coulombien. Elle est repérée par les trois nombres quantiques : \[n=1,~2,~\dots\quad;\quad l=0,~1,~2,~\dots,~(n-1)\quad;\quad m=-l,~\dots,~+l\]

L’énergie d’une solution dépend seulement du nombre quantique principal \(n\) : \[E_n=-\frac{E_1}{n^2}\qquad\text{avec~:}~~E_l=\frac{m_e~e^4}{2~\hbar^2}\approx 13,6~\rm eV\]

À chaque niveau d’énergie correspondent plusieurs valeurs possibles du moment cinétique.

La dégénérescence totale (en \(l\) et \(m\)) d’un niveau de \(n\) donné est : \[\sum_{l=0}^{n-1}~(2~l+1)~=n^2~\]

La fonction d’onde correspondant à un triplet donné (\(n,~l~,m\)) est unique (à la phase près) et s’exprime au moyen des coefficients des polynômes de Laguerre) :

\[\begin{aligned} \Psi_{n,l,m}(r)~&=~Y_{l,m}(\theta,\varphi)~\exp\Big(-\frac{r}{n~a_1}\Big)~\Big(\frac{r}{a_1}\Big)^l~\Big\{L_0+L_1\frac{r}{a_1}+\dots+L_{n-p-1}~\Big(\frac{r}{a_1}\Big)^{n-p-1}\Big\}\\ k~&=~0,~1,~\dots,~n-l-1\end{aligned}\]

3. Spectres de l’hydrogène

3.1. Représentation des énergies \(E_n\) (transitions d’états)

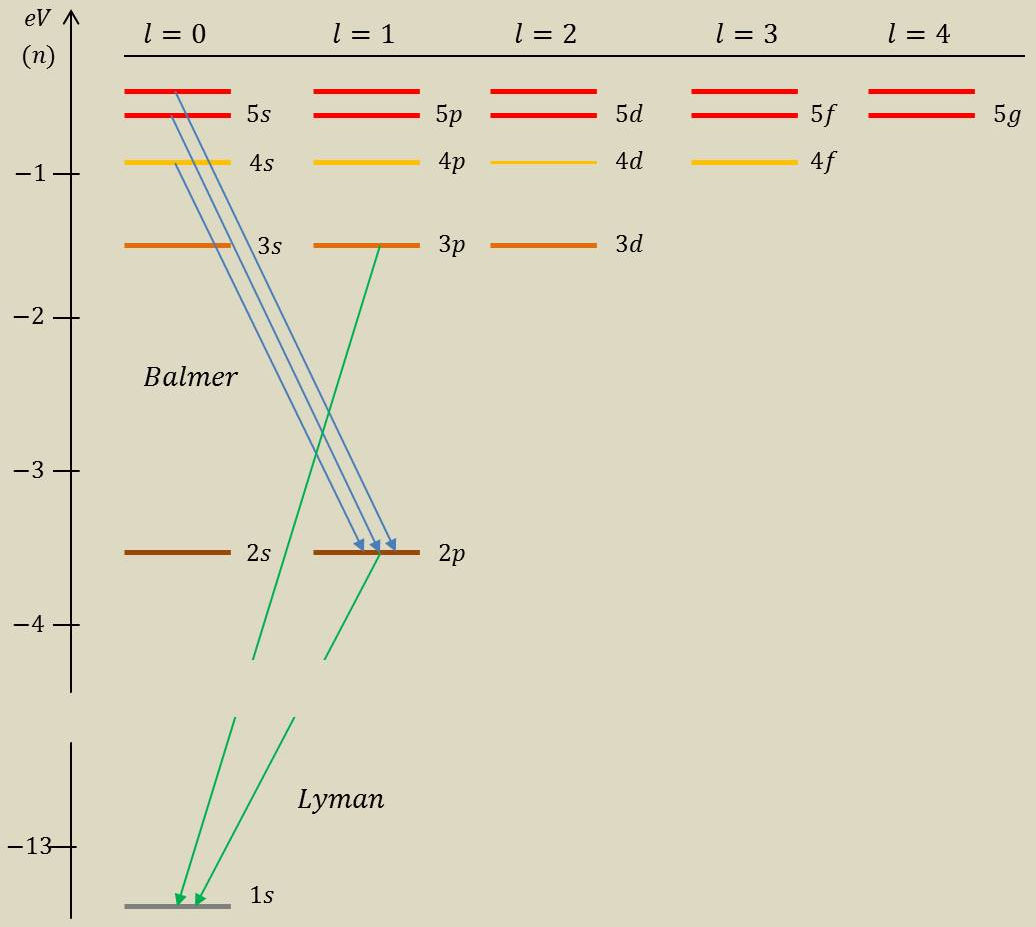Série de raies de Balmer : états \((ns)~\rightarrow (p)\)

\[\begin{aligned} \hbar~\omega&=E_n-E_2\\ &=13,6~\frac{n^2-4}{4~n^2}~\rm eV\end{aligned}\]

Premières raies (visible) :

\[\begin{aligned} \hbar~\omega&\approx 2~\text{à}~3~\rm eV\\ \lambda&\approx 0,5~\rm\mu m\end{aligned}\]

Série de raies de Lyman : transitions vers l’état fondamental (domaine UV) \[\lambda~\leq 121,5~\rm nm\]

 

3.2. États stationnaires de l’atome d’hydrogène

L’état fondamental (\(1s\) en spectroscopie) correspond à : \[n=1,~l=0,~m=0\]

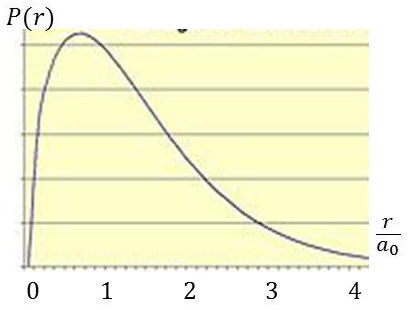
La figure ci-contre représente la densité de probabilité radiale \(P(r)\).

C’est la probabilité de trouver l’électron entre \(r\) et \(r+dr\) pour un atome d’hydrogène dans son état fondamental.

L’harmonique sphérique \(Y_{00}(\theta,~\varphi)\) étant constante et égale \(\cfrac{1}{\sqrt{4\pi}}\) , la fonction d’onde normalisée correspondant à cet état est : \[\Psi_{1,0,0}(r)~=~\frac{\exp(-\cfrac{r}{a_0})}{\sqrt{\pi~a_0^3}}\]

À titre documentaire, voici deux autres états (\(2s\) et \(2p\)) avec leurs fonction d’onde :

\[\begin{aligned} \text{niveau}~~2s~:~\Psi_{2,0,0}&=\frac{1}{\sqrt{8\pi~a_0^3}}~\Big(1-\frac{r}{2~a_0}\Big)~\exp\Big(-\frac{r}{2~a_0}\Big)\\ \text{niveau}~~2p~:~\Psi_{2,1,0}&=\frac{1}{\sqrt{32\pi~a_0^3}}~\frac{r}{a_0}~\cos\theta~\exp\Big(-\frac{r}{2~a_0}\Big)\\ \Psi_{2,1,\pm 1}&=\mp\frac{1}{64\pi~a_0^3}~\frac{r}{a_0}~\sin\theta~\exp\Big(-\frac{r}{2~a_0}\Big)~\exp(\pm~i~\varphi)\end{aligned}\]

La probabilité de trouver l’électron sur une coquille sphérique d’épaisseur \(dr\) sera : \[P(r)~dr~=~|\Psi_{1,0,0}(r)|^2~(4\pi~r^2)~dr\]

3.3. Autres états

Pour un niveau {\(n,l\)} la fonction : \[P(r)~=~|R_{n,l}(r)|~r^2\]

comporte un nombre \(n'=n-l-1\) de zéros (\(n'\) étant le degré du polynôme de Laguerre).

Pour \(l=n-1\), \(P(r)\) présente un maximum unique situé à une distance \(r=n^2~a_0\).

3.4. Dimension et ordre de grandeur

Considérons un atome d’hydrogène dans un état (\(n,~l,~m\)).

On peut montrer que la relation classique énergie cinétique – énergie potentielle reste valable pour les valeurs moyennes de ces quantités :

\[\begin{aligned} &E_n^{cin}~=~\Big\langle\frac{p^2}{2~m_e}\Big\rangle~=~-E_n~=~\frac{E_1}{n^2}\\ &E_n^{pot}~=~\Big\langle\frac{-e^2}{r}\Big\rangle~=~2~E_n~=~-\frac{2~E_1}{n^2}\end{aligned}\]

Pour les variations du rayon moyen avec \(n\) et \(l\) :

\[\begin{aligned} \langle r \rangle~&=~\frac{a_0}{2}~\{3~n^2-l(l+1)\}\\ \Big\langle\frac{1}{r}\Big\rangle~&=~\frac{1}{n^2~a_0}\\ \Big\langle\frac{1}{r^2}\Big\rangle~&=~\frac{2}{n^3~(2~l+1)~a_0^2}\\ \langle r^2 \rangle~&=~\frac{n^2~a_0^2}{2}~\{5~n^2+1-3~l~(l+1)\}\end{aligned}\]

Tous calculs faits :

\[\begin{aligned} &E_n^{cin}+E_n^{pot}=\frac{p+1}{n^2}~\langle \rho^l \rangle -(2~p+1)~\langle \rho^{l-1} \rangle +\frac{p}{4}~\{(2~l+1)^2-p^2\}~\langle \rho^{l-2} \rangle\\ &p>-2~l-1\qquad;\qquad\rho=\frac{r}{a_1}\end{aligned}\]

4. Atomes hydrogénoïdes

Un atome hydrogénoïde est un ion monoatomique ne possédant qu’un seul électron.

Les états d’un atome de rang \(Z\), ionisé (\(Z-1\)) fois, se déduisent des résultats précédents par la substitution : \[U(r)=-\frac{e^2}{r}\qquad\rightarrow\qquad U(r)=-\frac{Z~e^2}{r}\]

On retrouve la même forme que l’équation aux valeurs propres pour l’hydrogène mais les échelles des distances et d’énergie sont modifiées.

Les atomes hydrogénoïdes ont les mêmes fonctions d’onde que l’atome d’hydrogène, mais les dimensions sont réduites d’un facteur \(Z\) et les énergies sont multipliées par un facteur \(Z^2\) : \[a_1^{(Z)}=\frac{\hbar^2}{Z~m_e~e^2}\qquad;\qquad E_n^{(Z)}=-\frac{Z^2~m_e~e^4}{2~n^2~\hbar^2}\]

5. Appendice. Polynômes de Laguerre

Les polynômes de Laguerre sont les solutions de l’équation : \[xy''+(1-x)~y'+n~y=0\]

Équation différentielle linéaire et homogène d’ordre 2 pouvant s’écrire également : \[-\frac{d}{dx}\Big(x~e^{-x}~\frac{dy}{dx}\Big)=n~e^{-x}~y\]

Cette équation n’admet de solutions non singulières que si \(n\) est un entier positif.

Les solutions \(L_n\) forment une suite de polynômes orthogonaux dans \(\mathcal{L}^2(R^+,~e^{-x}~dx)\) formant une base orthonormale.

Cette suite de polynômes peut encore être définie par la formule de Rodrigues : \[L_n(x)~=~\frac{e^x}{n!}~\frac{d^n}{dx^n}~(e^{-x}~x^n)\]

Premiers polynômes de la suite des polynômes :

\[\begin{aligned} &n=0~: &&1\\ &n=1~: &&-x+1\\ &n=2~: &&\frac{1}{2}~(x^2-4~x+2)\\ &n=3~: &&\frac{1}{6}~(-x^3+9~x^2-18~x+6)\\ &n=4~: &&\frac{1}{24}~(x^4-16~x^3+72~x^2-96~x+24)\\ &n=5~: &&\frac{1}{120}~(-x^5+25~x^4-200~x^3+600~x^2-600~x+120)\\ &n=6~: &&\frac{1}{720}(x^6-36~x^5+450~x^4-2400~x^3+5400~x^2-4320~x+720)\end{aligned}\]