1. Notion d’activité radioactive
1.1. Expression de l’activité radioactive
L’activité \(A\), à une date donnée \(t\), d’un échantillon contenant \(N\) noyaux radioactifs est définie comme le nombre de noyaux qui se désintègrent par unité de temps (la seconde) : \[A(t)~=~-\frac{dN(t)}{dt}~=~\lambda~N(t)~=~\lambda~N_0~\exp(-\lambda~t)\]
Cette expression peut encore s’écrire :
\[\begin{aligned} A(t)~&=~A_0~\exp(-\lambda~t)~=~A_0~\exp(-t/\tau)\\ A_0~&=~\lambda~N_0\end{aligned}\]
Cette activité peut être exprimée en becquerels (Bq) (du nom du savant Becquerel). Elle est proportionnelle au nombre de noyaux radioactifs présents au même instant.
Une autre expression de \(A\) est intéressante en considérant deux relations :
– l’expression de la demi-vie : \[T_0~=~\frac{\ln(2)}{\lambda}~=~\frac{0,693}{\lambda}\]
– celle du nombre \(N_0\) d’atomes pour une masse \(m\) d’échantillon de masse molaire \(M\) : \[N_0~=~\frac{m~N}{M}\qquad;\qquad N = 6,02\times~10^{23}~:~\text{nombre d'Avogadro}\]
D’où cette deuxième expression dite équation d’activité \(A\) : \[A~=~\lambda~N_0~=~\ln(2)~\frac{N_0}{T_0}~=~0,693~\frac{N_0}{T_0}\]
On peut en conclure que cette activité est :
-
proportionnelle à ce nombre d’atomes ;
-
inversement proportionnelle à la demi-vie de l’isotope.
1.2. Exemple
Considérons un échantillon d’un gramme de radon. Le nombre correspondant d’atomes est : \[N_0~=~\frac{1\times 6,02\times~10^{23}}{222}~=~2,71\times 10^{21}~\rm atomes\]
La durée de demi-vie étant \(T_0\) = 3,824 jours. On obtient pour l’activité : \[A~=~\lambda~N_0~=~0,693~\frac{2,71\times~10^{21}}{3,824 \times 86~400}~=~5,75~\times~10^{15}~\rm Bq\]
1.3. Une autre unité d’activité radioactive : le curie
Le curie (Ci) correspond à l’activité de 1 g de radium Ra (du nom de Marie Curie). Cette unité première a un caractère historique et mérite d’être conservée.
On a pu établir que la constante de conversion de l’activité exprimée en nombre de désintégrations par seconde (becquerels) a pour valeur : \[1~\rm Ci~=~3,7\times 10^{10}~Bq\]
Voir son application dans les exercices proposés.
2. Datation au carbone 14
Le \(^{14}\)C disparaît progressivement de la matière organique à partir de sa mort. Exemple connu : fragments de tissu de lin trouvés dans un habitat préhistorique.
Par combustion, on a obtenu du CO\(_2\) une activité de 241 désintégrations par heure et par litre. Avec un tissu similaire, fabriqué de nos jours, l’activité est de 492. On sait que le \(^{14}C\) a une période de 5730 ans.
On applique la loi de désintégration :
\[\begin{aligned} N~&=~N_0~\exp(-\lambda~t)~=~N_0~\exp\Big(-\frac{t}{T}~\ln 2\Big)\\ \ln\Big(\frac{N_0}{N}\Big)~&=~\frac{t}{T}~\ln 2\end{aligned}\]
En tenant compte que l’activité d’un échantillon est proportionnelle au nombre d’atomes qu’il contient :
\[\begin{aligned} \frac{A_0}{A}~&=~\frac{N_0}{N} \\ t~&=~T~\frac{\ln(A_0/A)}{\ln~2}~=~5730~\frac{\ln(492/241)}{\ln(2)}~=~5900~\text{ans}\end{aligned}\]
Remarque
Le carbone naturel est composé de deux isotopes stables : le \(^{12}\)C pour 98,892 % et le \(^{13}\)C pour 1,108 %.
Le carbone\(~^{14}\)C n’existe pas à l’état naturel. Il est en fait produit en haute atmosphère par capture neutronique (action de neutrons cosmiques sur le \(~^{13}\)C) : \[~^{13}{\rm C} + n + \rm rayon~\gamma\quad\rightarrow\quad^{14}C\]
Du \(^{14}\)C est produit continument en haute atmosphère. Il se désintègre ensuite sur une période de 5730 ans.
La concentration en \(^{14}\)C s’équilibre lorsque le taux de production est égal au taux de disparition (désintégration). Autrement, on ne trouverait que du \(^{14}\)C. Il se forme environ 2,5 atomes de \(^{14}\)C par seconde et par cm² de surface terrestre.
3. Âge des roches anciennes
Le thorium 232 (période T de 14 milliards d’années) est l’élément père d’une famille radioactive dont le dernier terme est le plomb 208. Les éléments intermédiaires sont tous de période négligeable.
Dans les roches les plus anciennes de la Terre où le thorium et le plomb sont associés, on trouve un rapport moyen de 7 grammes de thorium pour 1 gramme de plomb.
En admettant que tout le plomb provienne de la désintégration du thorium, on se propose de calculer l’âge de ces roches.
Le nombre initial d’atomes de thorium au moment de la formation des roches est \(N_0\). Le nombre d’atomes restant à l’instant \(t\) est : \[N~=~N_0~\exp~(\lambda~t)\]
Le nombre d’atomes de plomb formés (\(N_0~-~N\)) est égal au nombre d’atomes de thorium désintégrés. D’où le rapport de masse : \[\frac{\rm Th}{\rm Pb}~=~\frac{232~N}{208~(N_0-N)}\]
En divisant haut et bas par \(N\), il vient : \[\frac{\rm Th}{\rm Pb}~=~\frac{232}{208~\{\exp(\lambda~t)-1\}}~=~7\]
On obtient : \[\exp(\lambda~t)~=~1,159\quad\Rightarrow\quad\lambda~t~=~\ln(1,159)~=~0,1479\]
Sachant que : \[\lambda~=~\frac{\ln 2}{T}\]
On obtient, tous calculs faits : \[t~=~\frac{0,1479\times 14}{0,693}~=~2,99~\text{milliards d'années}\]
La méthode ne donne pas l’âge de la Terre, mais la date de formation des roches (moment où la Terre s’est refroidie et où la croûte terrestre est apparue).
4. Âge du système solaire
Une méthode consiste à utiliser la teneur relative des roches terrestres et des météorites en \(^{86}\)Sr, \(^{87}\)Sr et \(^{87}\)Rb de durée de vie \(t~=~6,8~\times 10^{10}\) ans et qui se désintègre en \(^{87}\)Sr.
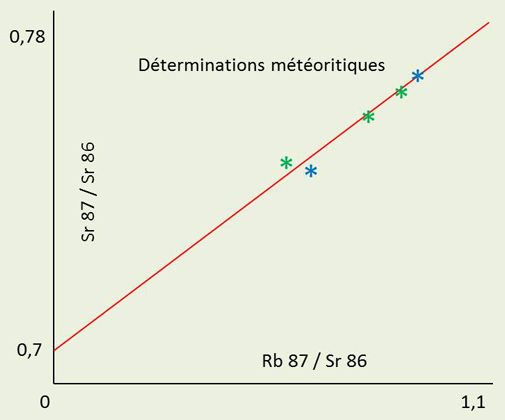La figure ci-contre montre le diagramme \(\rm ^{87}Sr / ^{86}Sr\) en fonction de \(\rm ^{87}Rb / ^{86}Sr\), déterminé dans différents échantillons terrestres ou météorites.
Ces valeurs (expérimentales) sont disposées suivant une droite. Sa pente a pour expression : \[\exp\{(t_s/\tau)-1\}\]
-
\(t_s\) : âge du système solaire
-
\(\tau\) : durée de vie du noyau radioactif \(^{87}\)Rb
Connaissant \(\tau\), on détermine de façon très précise l’âge du système solaire :
\[t_s~=~4,54\times 10^9~\rm ans\]
Résultat en accord avec celui obtenu par la théorie de l’évolution stellaire.
