1. Établissement de l’équation

L’équation des cordes vibrantes est l’équation fondamentale pour tout phénomène physique de propagation.

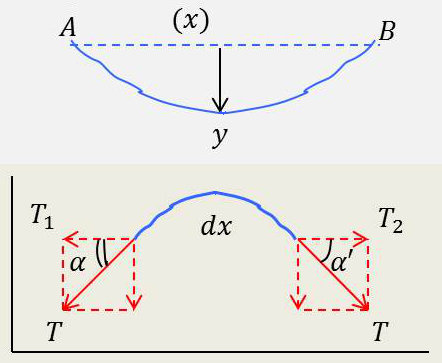– Le poids de la corde est négligé, mais pas sa masse.

– On suppose que la corde est sans raideur, c’est-à-dire que le module de la tension est constant le long de la corde.

– On suppose petite l’amplitude des mouvements (donc les angles).

– On désigne par \(m\) la masse par unité de longueur.

On a donc :

\[\begin{aligned} &y(x,~t)\quad;\quad\gamma=\frac{\partial^2y}{\partial t^2}\\ &m~\gamma=\mu~dx~\frac{\partial y}{\partial t^2}=T_1-T_2\approx T~(\alpha'-\alpha)\end{aligned}\]

Les deux angles, associés aux tangentes représentent des pentes et en appliquant le théorème des accroissements finis : \[y~\alpha=\frac{\partial y}{\partial x}\quad;\quad\alpha'=\alpha+\frac{\partial}{\partial x}\Big(\frac{\partial y}{\partial x}\Big)~dx\]

Par suite : \[\mu~dx~\frac{\partial^2y}{\partial t^2}=T~\frac{\partial^2y}{\partial x^2}\quad\Rightarrow\quad\frac{\partial^2y}{\partial t^2}=\frac{T}{\mu}~\frac{\partial^2y}{\partial x^2}\]

Ce qui peut encore s’écrire : \[\frac{\partial^2y}{\partial t^2}=\frac{T}{\mu}~\frac{\partial^2y}{\partial x^2}=\frac{1}{a^2}~\frac{\partial^2y}{\partial x^2}\quad;\quad a=\sqrt{\frac{\mu}{T}}\]

En considérant le paramètre \(r=\pm(1/a)\), solution de l’équation caractéristique, on aboutit à la solution superposition de deux ondes aller - retour : \[y(x,~t)=\varphi(x+a~t)+\psi(x-a~t)\]

Il faut adapter cette solution générale aux conditions initiales et aux conditions aux limites :

• initiales : forme de la corde, état des vitesses à l’instant \(t=0\) ;

• limites : points \(A\) et \(B\) au repos quelque soit \(t\).

2. Problème des conditions initiales

Pour \(t=0\), on se donne :

• la forme de la corde : \(~y(x,~0)=g(x)\)

• les vitesses : \(\quad\qquad\cfrac{\partial y}{\partial t}(x,~0)=h(x)\)

On doit donc écrire que :

\[\begin{aligned} \varphi(x)+\psi(x)&=g(x)\\ a~\varphi'(x)-a~\psi'(x)&=h(x)\quad\Rightarrow\quad a~\{\varphi(x)-\psi(x)\}=\int_0^x h(s)~ds\end{aligned}\]

En faisant la somme et la différence des deux expressions, il vient :

\[\begin{aligned} &\varphi(x)=\frac{1}{2}~\{g(x)+\frac{1}{a}\int_0^x h(s)~ds\}\\ &\psi(x)=\frac{1}{2}~\{g(x)-\frac{1}{a}\int_0^x h(s)~ds\}\end{aligned}\]

Dans l’hypothèse où la corde initialement au repos est abandonnée sans vitesse initiale : \[\varphi(x)=\psi(x)=\frac{1}{2}~g(x)\]

3. Propagation d’un ébranlement

La solution pour la propagation d’un ébranlement est du type : \[y(x,~t)=\varphi(x+c~t)+\psi(x-c~t)\]

Elle convient à la propagation du son, de la lumière, etc., le terme \(c\) étant la vitesse de propagation. L’onde \(\varphi\) se déplace vers la droite et l’onde \(\psi\) vers la gauche.

Étudions à présent le problème de la réflexion pour une onde se déplaçant entre les points d’abscisse \(0\) et \(l\). Nous allons mettre en évidence la périodicité et le changement de signe à la réflexion.

On suppose que (conditions aux limites) : \[y(0,~t)=0\quad;\quad y(l,~t)=0\]

Adoptant la solution générale :

\[\begin{aligned} &\varphi(a~t)+\psi(-a~t)=0\\ &\varphi(l+a~t)+\psi(l-a~t)=0\end{aligned}\]

Posons : \[a~t=u\quad;\quad l-a~t=v\]

On a alors :

\[\begin{aligned} &\varphi(u)+\psi(-u)=0\\ &\varphi(2~l+v)+\psi(-v)=0\end{aligned}\]

Faisant \(u=v\) : \[\varphi(u)=\varphi(2~l+u)\quad\Rightarrow\quad\varphi~\text{périodique }~2~l\]

On démontrerait de même que : \[\psi(u)=\psi(2~l+u)\quad\Rightarrow\quad\psi~\text{périodique }~2~l\]

Partant maintenant de la forme générale : \[\varphi(a~t)+\psi(-a~t)=0\qquad\text{soit~:}\quad\varphi(x)+\psi(-x)=0\]

Sachant que : \[\varphi(x)=\psi(x)=\frac{1}{2}~g(x)\]

on en déduit que : \[\varphi(x)=-\psi(-x)=0\]

ce qui montre bien qu’il y a changement de signe à la réflexion.

4. Méthode de Bernouilli

La méthode de Bernouilli est beaucoup plus physique. On part donc de l’équation de propagation : \[\frac{\partial^2y}{\partial t^2}=\frac{1}{c^2}~\frac{\partial^2y}{\partial x^2}\]

avec les conditions initiales : \[y(x,~0)=g(x)\quad;\quad\frac{\partial y}{\partial t}(x,~0)=h(x)\]

et les conditions aux limites : \[y(0,~t)=0\quad;\quad y(l,~t)=0\]

La recherche des solutions élémentaires se fait par séparation des variables. C’est à dire que l’on pose : \[y(x,~t)=X(x)~T(t)\]

On obtient alors : \[\frac{\partial^2y}{\partial t^2}=X~T''\quad\text{et}\quad\frac{\partial^2x}{\partial t^2}=T~X''\]

Et en revenant à l’équation de départ : \[\frac{X''}{X}=\frac{1}{c^2}~\frac{T''}{T}\]

Cette relation doit être vraie quelque soient \(x\) et \(t\) . C’est une constante que l’on posera égale à \((-\beta^2)\). Il y a séparation des variables :

\[\begin{aligned} X''+\beta^2~X=0 &\quad\Rightarrow\quad X= \begin{Bmatrix} sin\\ cos \end{Bmatrix} \beta~x \\ T''+c^2~\beta^2~T=0 &\quad\Rightarrow\quad T= \begin{Bmatrix} sin\\ cos \end{Bmatrix} c~\beta~t\end{aligned}\]

D’où la solution très particulière : \[y(x,~t)= \begin{Bmatrix} sin\\ cos \end{Bmatrix} \beta~x~~ \begin{Bmatrix} sin\\ cos \end{Bmatrix} c~\beta~t\]

4.1. Adaptation aux conditions aux limites

Nous avons aux limites :

\[\begin{aligned} y(0,~t)=0\quad&\Rightarrow\quad\sin\beta~x~~ \begin{Bmatrix} sin\\ cos \end{Bmatrix} c~\beta~t \\ y(l,~t)=0\quad&\Rightarrow\quad\sin\beta~l=0\quad;\quad\beta=\frac{k~\pi}{l}\end{aligned}\]

Les solutions particulières sont alors : \[y(x,~t)=\sin\frac{k~\pi}{l}~x~~ \begin{Bmatrix} sin\\ cos \end{Bmatrix} k~\frac{c~\pi}{l}~t\]

Quelle est la signification physique de \(\beta\) ?

Quand une corde vibre, elle peut présenter 1, 2..., \(k\) fuseaux (si elle est attachée aux deux bouts). La distance entre deux nœuds est \(l=k~\lambda/2\), or \(\beta=k~\pi/l\), c’est-à-dire \(\beta=2~\pi/\lambda\) et on reconnaît le nombre d’onde.

4.2. Adaptation aux conditions initiales

Une somme de combinaisons linéaires de solutions particulières doit satisfaire aux conditions initiales.

On écrit :

\[\begin{aligned} y(x,~t)=\sum_{k=l}^{\infty}B_k~\sin\frac{k~\pi}{l}~x~~\sin\frac{k~c\pi}{l}~t\\ +\sum_{k=l}^{\infty}C_k~\sin\frac{k~\pi}{l}~x~~\cos\frac{k~c~\pi}{l}~t\end{aligned}\]

et il faut déterminer les constantes \(B\) et \(C\).

Si l’on fait \(t=0\), il vient : \[g(x)=\sum_{k=1}^{\infty}C_k~\sin\frac{k~\pi}{l}~x\]

On reconnaît immédiatement les coefficients de série de Fourier et comme \(g(x)\) est connue : \[C_k=\frac{2}{l}\int_0^lg(x)~\sin\frac{k~\pi~x}{c}~dx\]

On a alors :

\[\begin{aligned} h(x)=\Big(\frac{\partial y}{\partial t}\Big)_{x,~0}=\sum_{k=1}^{\infty}B_k~\frac{kc\pi}{l}~\sin\frac{k~\pi}{l}~x =\frac{c~\pi}{l}~\sum_{k=1}^{\infty}k~B_k~\sin\frac{k~\pi}{l}~x\end{aligned}\]

Et en fin de compte : \[h~B_k=\frac{2}{l}~\int_0^l h(x)~\sin\frac{k~\pi}{l}~x~dx\]

\(C_k\) et \(B_k\) sont les coefficients de l’harmonique de rang \(k\), sachant que la valeur \(k=1\) correspond à la fondamentale.