1. Propagation des déformations transversales
Nous avons déjà étudié les déformations longitudinales des verges ; passons maintenant à l’étude des déformations transversales (ce sera, par exemple, le type de vibration des branches d’un diapason).
1.1. Relations de base
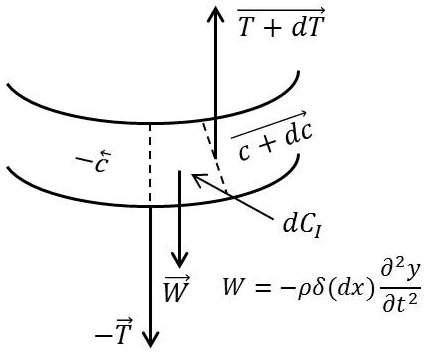Écrivons les équations d’équilibre d’un élément \(dx\) de la verge sous l’action des forces appliquées et des forces d’inertie et examinons, dans ce but, le déplacement, à l’instant \(t\) de l’élément \(dx\).
Ce déplacement comprend :
– un déplacement vertical du centre de gravité, d’où apparition d’une force d’inertie : \[-\rho~S~dx~\frac{\partial^2y}{\partial t^2}\]
– une rotation d’un angle \(\alpha\) qui est le même que celui des génératrices (pratiquement), car la déformation des sections droites est faible et elles coupent normalement les génératrices à la surface de la barre.
D’où apparition d’un couple d’inertie : \[dC_I=-\rho~I~dx~\frac{\partial^2\alpha}{\partial t^2}\]
L’existence de ce couple nous oblige à modifier les relations établies plus haut entre les efforts tranchants et le moment fléchissant. Nous devons maintenant écrire : \[T~dx+dC=-dC_I=+\rho~I~dx~\frac{\partial^2\alpha}{\partial t^2}\]
et non plus égale à 0, comme c’était le cas dans la flexion statique où aucun couple n’était directement appliqué aux diverses sections par le champ de forces extérieur.
Il en résulte : \[T=\rho~I~\frac{\partial^2\alpha}{\partial t^2}-E~I~\frac{\partial^2\alpha}{\partial t^2}\qquad \text{car :}\quad C=E~I~\frac{\partial\alpha}{\partial x}\]
Écrivons maintenant que la résultante des forces appliquées est égale à l’opposé de la force d’inertie : \[\rho~S~dx~\frac{\partial^2\alpha}{\partial t^2}=dT=\frac{\partial T}{\partial x}~dx\]
Soit, en simplifiant par \(dx\) : \[\rho~S~\frac{\partial^2\alpha}{\partial t^2}=-E~I~\frac{\partial^3\alpha}{\partial x^3}+\rho~I~\frac{\partial^3\alpha}{\partial t^2~\partial x}\]
Et en remplaçant \(\alpha\) par \(\cfrac{\partial y}{\partial x}\) (l’angle dont a tourné la section est le même que celui dont a tourné la fibre neutre ou une génératrice quelconque) : \[\rho~S~\frac{\partial^2y}{\partial t^2}=-E~I~\frac{\partial^4y}{\partial x^4}+\rho~I~\frac{\partial^4y}{\partial t^2~\partial x^2}\]
Montrons que ce dernier terme est négligeable dans le cas d’une oscillation sinusoïdale de longueur d’onde \(\lambda\) grande devant le diamètre de la barre. Cela revient à montrer que ce dernier terme est négligeable devant le premier membre de l’équation, ou encore qu’il en est de même des quantités obtenues en intégrant deux fois par rapport à \(t\) (il s’agit en effet, de termes oscillants à la même fréquence).
Il suffit donc de montrer que : \[\frac{I}{S}~\frac{1}{y}~\frac{\partial^2y}{\partial x^2}~\ll~1\]
Or, la quantité \(\cfrac{1}{y}~\cfrac{\partial^2y}{\partial x^2}\) est de l’ordre de \(\cfrac{1}{\lambda^2}\) et la quantité \(\cfrac{I}{S}\) est de l’ordre du carré du diamètre de la barre puisqu’elle est égale au carré de son rayon de giration.
Nous pouvons donc négliger ce second terme tant que \(\lambda\) est très supérieur au diamètre de la barre et écrire simplement l’équation : \[\rho~S~\frac{\partial^2y}{\partial t^2}=-E~I~\frac{\partial^4y}{\partial x^4}\]
Ce que nous aurions obtenu directement en négligeant d’emblée le couple d’inertie de rotation, écrivant que l’accélération verticale de l’élément \(dx\) est fournie par la force \(dT\) et utilisant l’expression de \(T\) obtenue plus haut dans le cas de la flexion statique (pas de couples extérieurs appliqués directement à l élément \(dx\)).
1.2. Vitesse de phase
L’équation de propagation des mouvements de la barre s’écrit dès lors : \[\frac{\partial^2y}{\partial t^2}=-\frac{E~I}{\rho~S}~\frac{\partial^4y}{\partial x^4}\]
Elle est donc d’un type que nous n’avons pas rencontré jusqu’ici. Décrivons-la sous une forme plus simple, en introduisant le rayon de giration \(r=\sqrt{I/S}\) de la section droite et la vitesse de propagation \(c_0=\sqrt{E/\rho}\) des ondes longitudinales. Il vient : \[\frac{\partial^2y}{\partial t^2}=-c_0^2~r^2~\frac{\partial^4y}{\partial x^4}\]
Cherchons la vitesse de phase \(c\) d’une onde transversale de pulsation \(\omega\) et d’équation : \[y=a~\exp j~\omega~(t-x/c)\]
Nous obtenons : \[\frac{\partial^2y}{\partial t^2}=-\omega^2~y\quad;\quad\frac{\partial^4y}{\partial x^4}=y~\frac{\omega^4}{c^4}\]
L’équation aux dérivées partielles exige donc la relation : \[\frac{c^4}{\omega^4}=c_0^2~r^2\]
Soit en introduisant la longueur d’onde \(\lambda=\cfrac{2~\pi~c}{\omega}\) : \[c^2~\frac{\lambda^2}{4}~\pi^2=c_0^2~r^2\qquad\text{ou}\qquad c=c_0~\frac{2~\pi~r}{\lambda}\]
La vitesse de propagation de la phase varie donc en raison inverse de la longueur d’onde ; de plus, comme \(\cfrac{r}{\lambda}\ll 1\) (hypothèse simplificatrice initiale), cette vitesse \(c\) de propagation de la phase dans les vibrations transversales est très inférieure à la vitesse de propagation des ondes longitudinales \(c_0\) .
1.3. Vitesse de groupe
Nous venons de rencontrer un exemple de propagation d’ondes où la vitesse de phase varie avec la fréquence, ou, ce qui revient au même, avec la longueur d’onde. La dispersion n’est pas ici liée à un phénomène d’absorption, comme c’était le cas, dans un certain domaine de fréquences, pour les ondes planes ultrasonores dans les gaz polyatomiques ; elle résulte de la forme particulière de l’équation de propagation.
La conséquence de cette dispersion est l’apparition d’une vitesse de groupe différente de la vitesse de phase \(c\). L’expression de la vitesse de groupe : \[U=c-\lambda~\frac{dc}{d\lambda}\quad;\quad c=c_0~\frac{2~\pi~r}{\lambda}\]
nous conduit ici (en admettant, bien entendu, qu’il n’y a pas dispersion pour la vitesse de phase \(c_0\) des ondes planes longitudinales dans le milieu indéfini) à : \[\frac{dc}{d\lambda}=-\frac{c}{\lambda}\qquad\text{ou plus simplement~:}\quad U=2~c\]
2. Vibrations propres d’une verge de longueur finie
Soit \(l\) la longueur de la verge ; nous allons chercher si elle peut être le siège de vibrations stationnaires, chacune de ses sections subissant un mouvement sinusoïdal d’amplitude variable d’une section à l’autre, mais de phase identique pour toutes les sections.
Ceci revient à chercher une solution de l’équation aux dérivées partielles : \[\frac{\partial^2y}{\partial t^2}=-c_0^2~r^2~\frac{\partial^4y}{\partial x^4}\]
qui soit de la forme, l’origine des temps étant convenablement choisie : \[y(x,~t)=f(x)~\cos\omega~t\]
On montrerait d’ailleurs immédiatement, comme dans le cas des vibrations propres de fluides enfermés dans les cavités, que le simple fait d’écrire le déplacement \(y(x,~t)\) sous la forme \(y(x,~t)=f(x)~\cos\omega~t\) exige que la fonction \(g(t)\) soit une fonction sinusoïdale si le mouvement doit persister au cours du temps.
La substitution donne immédiatement : \[-\omega^2~f(x)~\cos\omega~t=-c_0^2~r^2~\frac{d^4f}{dx^4}~\cos\omega~t\]
En posant \(m^2=\cfrac{\omega}{c~r}\) , elle s’écrira : \[\frac{d^4f}{dx^4}=m^4~f\qquad\text{équation aux amplitudes}\]
La solution est une combinaison de quatre solutions linéairement indépendantes que nous obtenons immédiatement sous forme exponentielle : \[e^{m~x}~;~e^{-m~x}~;~e^{j~m~x}~;~e^{-j~m~x}\]
Quatre autres solutions indépendantes peuvent aussi être représentées par des combinaisons linéaires de ces quatre exponentielles : \[\cosh(m~x)~;~\sinh(m~x)~;~\cos(m~x)~;~\sin(m~x)\]
La solution générale pour la fonction \(f(x)\) représentant la distribution des amplitudes le long de la verge vibrante est donc de la forme : \[f(x)=A~\cosh(m~x)+B~\sinh(m~x)+C~\cos(m~x)+D~\sin(m~x)\]
et pour y, avec \(\omega=c_0~r~m^2\) : \[y(x,~t)=\{A~\cosh(m~x)+B~\sinh(m~x)+C~\cos(m~x)+D~\sin(m~x)\}~\cos\omega~t\]
Les constantes \(A,~B,~C,~D\) sont à ajuster d’après les conditions imposées à la barre ; nous entendons par là les conditions imposées de façon permanente aux amplitudes vibratoires et non pas à l’instant \(t=0\).
Nous allons trouver un certain nombre de mouvements sinusoïdaux possibles ; le mouvement le plus général sera donc une superposition de ces mouvements sinusoïdaux avec des phases respectives et des amplitudes qu’il conviendrait ensuite d’ajuster pour satisfaire aux conditions initiales (forme de la verge et vitesse de ses divers éléments à l’instant \(t=0\) comme nous l’avons fait pour les cordes vibrantes (corde pincée ou corde frappée).
Nous envisagerons un seul cas (simple) de conditions imposées de façon permanente à la verge ; nous choisirons le cas où la verge est encastrée en \(x=0\) et libre en \(x=l\).
L’encastrement en \(O\) impose : \[y=0~~;~~y'=0\qquad\text{pour :}\quad x=0~~~\forall~t\]
Nous avons vu plus haut que les efforts tranchants n’imposent aucun glissement d’ensemble des sections droites.
Soit : \[f(0)=f'(0)=0\quad\Rightarrow\quad A+C=0~~~\text{et}~~~m~(B+D)=0\]
Donc : \[C=-A~~~\text{et}~~~D=-B\]
Par suite : \[f(x)=A~\{\cosh(m~x)-\cos(m~x)\}+B~\{\sinh(m~x)-\sin(m~x)\}\]
du seul fait de l’encastrement en \(O\) (section droite en \(x=0\) soudée à une surface indéformable).
La verge est libre en \(x=l\), ce qui entraîne un moment fléchissant et un effort tranchant nuls en ce point. Cela exige : \[\frac{\partial^2y}{\partial x^2}=0~~~\text{et}~~~\frac{\partial^3y}{\partial x^3}=0\qquad\forall~t~~\text{pour}~~x=l\]
Soit : \[f''(l)=f'''(l)=0\]
Par suite :
\[\begin{aligned} m^2A~\{\cosh(m~l)+\cos(m~l)]+m^2~B~\{\sinh(m~l)+\sin(m~l)\}=0\\ m^3A~\{\sinh(m~l)-\sin(m~l)]+m^3~B~\{\cosh(m~l)+\cos(m~l)\}=0\end{aligned}\]
Ce système d’équations linéaires et homogènes en \(A\) et \(B\) n’a de solutions non nulles que si pour le déterminant : \[\{\cosh(m~l)+\cos(m~l)\}^2-\{\sinh^2(m~l)-\sin^2(m~l)\}=0\]
En remarquant que : \[\cosh^2-\sinh^2=\cos^2+\sin^2=1\]
il vient : \[2+2~\cosh(m~l)~\cos(m~l)=0\quad\Rightarrow\quad\cosh(m~l)=-\frac{1}{\cos(m~l)}\]
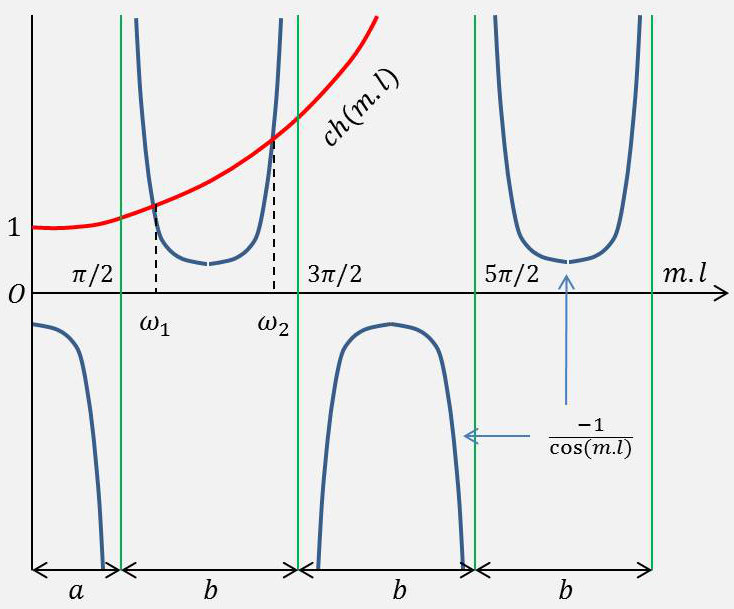Les solutions de cette équation ne peuvent être obtenues que par résolution graphique (voir figure ci-contre).
À chacune des intersections des deux courbes correspond une valeur possible de la quantité \((ml)\), c’est à dire de la pulsation \(\omega\) qui est donnée par la relation : \[\omega=\frac{c_0~r}{l^2}~(m~l)^2\]
Les valeurs acceptables de \((m~l)\) sont sensiblement de la forme : \[(2~k+1)~\frac{\pi}{2}\]
sauf la première qui est nettement supérieure à \(\cfrac{\pi}{2}\).
Il s’ensuit que les vibrations partielles successives ne constituent pas les harmoniques d’un même fondamental ; leurs fréquences varient sensiblement comme les inverses des carrés des nombres impairs successifs, sauf en ce qui concerne les toutes premières.
Un diapason accordé sur une fréquence déterminée et fixé à une caisse de résonance oscillera, en principe, sur tous les modes de vibration qui ne présentent pas de nœuds au point d’attaque (analogie avec le calcul fait pour les cordes vibrantes). Toutefois, la caisse de résonance ne renforcera pas le fondamental, les partiels du diapason n’entrant pas dans la série de ceux de la caisse.
