1. Rappel mathématique sur les tenseurs

1.1. Composantes contravariantes d’un tenseur

Soit un espace vectoriel \(E_n\) et deux bases \(\vec{e}_\alpha\) et \(\vec{e}_\alpha'\). Un vecteur \(\overrightarrow{V}\in E_n\) possède deux composantes contravariantes, \(v^{\alpha}\) dans \(\overrightarrow{e}_\alpha\) et \(v^{\alpha'}\) dans \(\overrightarrow{e}_\alpha'\) : \[\vec{V}=v^{\alpha}~\overrightarrow{e}_\alpha=v^{\alpha'}~\overrightarrow{e}_{\alpha'}\]

Les vecteurs \(\overrightarrow{e}_\alpha\) et \(\overrightarrow{e}_{\alpha'}\) sont des vecteurs libres dans leurs bases respectives. Il existe une transformation linéaire régulière \(A\) telle que : \[\overrightarrow{e}_{\alpha'} = A^\beta _{\alpha'}~\overrightarrow{e}_{\beta}\quad;\quad \overrightarrow{e}_{\beta'} = A^\alpha _{\beta'}~\overrightarrow{e}_{\alpha}\] \[A^{\alpha} _{\beta}= \frac{\min(A^{\alpha} _{\beta'})}{|\det\ A|}\]

Il s’ensuit que : \[v^{\alpha'}=A^{\alpha'} _{\beta}~v^{\beta}\quad;\quad v^{\beta'}=A^{\beta'} _{\alpha}~v^{\alpha}\]

1.2. Produit scalaire

Un espace vectoriel \(E_n\) est euclidien si on définit sur cet espace \(E_n\) un produit scalaire : \[\overrightarrow{x}=x^{\alpha}~\overrightarrow{e}_{\alpha}\quad;\quad \overrightarrow{y}= y^{\beta}~\overrightarrow{e}_{\beta}\] \[\overrightarrow{x}\cdot\overrightarrow{y}=x^{\alpha}~y^{\beta}~(\overrightarrow{e}_{\alpha}\cdot\overrightarrow{e}_{\beta})=x^{\alpha}~y^{\beta}~g_{\alpha\beta} \qquad\text{avec :}\quad g_{\alpha\beta}\neq 0\]

1.3. Composantes covariantes d’un tenseur

On sait les composantes covariantes d’un tenseur définir dès lors que l’on a su définir un produit scalaire : \[v_{\alpha}=\overrightarrow{V}\cdot\overrightarrow{e}_{\alpha}= (v^{\beta}~\overrightarrow{e}_{\alpha})\cdot\overrightarrow{e}_{\alpha}= v^{\beta}~(\vec{e}_{\beta}\cdot\overrightarrow{e}_{\alpha})=g_{\alpha \beta}~v^\beta\]

Cette formule est inversible, car \(g_{\alpha \beta}\) est non dégénérée : \[v^{\beta}=\frac{\min (g_{\alpha \beta})}{g}.v_\alpha \ \ \ \ avec\ \ g\neq 0\]

Par définition : \[g^{\beta \alpha }=\frac{1}{g}~g_{\alpha \beta}\quad\Rightarrow\quad v^{\beta}=g^{\beta \alpha}~v_{\alpha}\]

1.4. Espace affine \(E^{(a)}_n\) associé à l’espace vectoriel \(E_n\)

Un espace affine \(E^{(a)}_n\) est un espace constitué de points ; \(E^{(a)}_n\) est associé à \(E_n\) si les axiomes suivants sont respectés :

• Au couple \((A,B)\in E^{(a)}_n\), on associe \( \overrightarrow{AB}=-\overrightarrow{BA}\quad\Rightarrow\quad\overrightarrow{AB}=\vec{AC}+ \overrightarrow{CB} \).

• Il existe un point \(O\) tel que, au point \(A\), on associe \(\overrightarrow{OA}\).

On peut alors définir un repère en espace affine. Il est constitué par le point \(O\) et la base de l’espace vectoriel associé.

1.5. Changement de repère en espace affine

Les coordonnées de \(A\) par rapport à \(O\) sont les composantes de \(\overrightarrow{OA}\) dans le repère d’origine \(O\). On recherche celles de \(A\) par rapport à \(O'\) : \[\overrightarrow{OA}=A^{\alpha}~\overrightarrow{e}_{\alpha}\quad;\quad \overrightarrow{OO'}=B^{\alpha}~\overrightarrow{e}_{\alpha}\]

Le changement de base est défini par une matrice \(M\): \[\overrightarrow{e}_{\alpha'}=M^{\beta}_{\alpha '}~\overrightarrow{e}_{\beta}\]

On peut écrire \(\overrightarrow{O'A}=\overrightarrow{OA}-\overrightarrow{OO'}\), soit : \[A^{\alpha'}~\overrightarrow{e}_{\alpha'}=A^{\alpha}~\overrightarrow{e}_{\alpha}-B^{\alpha}~\overrightarrow{e}_{\alpha}\] \[A^{\alpha'}~M^{\beta}_{\alpha'}~\overrightarrow{e}_{\beta}=A^{\beta}~\overrightarrow{e}_{\beta}-B^{\beta}~\overrightarrow{e}_{\beta}\]

d’où : \[A^{\beta}=B^{\beta}+M^{\beta}_{\alpha'}~A^{\alpha'}\]

2. Espace ponctuel euclidien

C’est un espace affine associé à un espace vectoriel euclidien. On peut y définir un produit scalaire. Étant donné deux points \(M\) et \(N\), on sait définir : \[\overrightarrow{MN}~~\text{et}~~s^2=\overrightarrow{MN}\cdot\overrightarrow{MN}\]

Dans un repère \((\overrightarrow{e}_{\alpha},~O)\) on a : \[M:~x^{\alpha},~y^{\alpha}\quad;\quad N:~x^{\beta},~y^{\beta}\] \[S^2=g_{\alpha\beta}~(y^{\alpha}-x^{\alpha})~(y^{\alpha}-x^{\alpha})\]

On peut également écrire : \[ds^2=dx^{\alpha}~dx_{\beta}=g_{\alpha\beta}~dx^{\alpha}~dx^{\beta}\] On distingue deux types d’espaces euclidiens : l’espace proprement euclidien et l’espace improprement euclidien. La matrice \(g\) est symétrique, donc toujours diagonalisable et ses valeurs propres sont toujours réelles.

Si toutes les valeurs propres sont positives, l’espace est alors proprement euclidien. Tel est le cas des coordonnées cartésiennes et telles que : \[ds^2=(dx^1)^2+(dx^2)^2+\dots+(dx^n)^2\]

S’il y a des valeurs propres positives et des valeurs propres négatives, l’espace est improprement euclidien. On obtient par exemple pour les coordonnées :

\[ds^2=(dx^1)^2-(dx^2)^2+\dots+(dx^n)^2\]

Le symbole [+ + – – + – + + +] indique le nombre respectif de valeurs propres positives et négatives. C’est la signature de l’espace. Dans le cas de l’espace \(E_4\) à signature hyperbolique [+ – – –] : \[g_{\alpha\beta}= \begin{pmatrix} 1& & & \\ &-1& & \\ & &-1& \\ & & &-1 \end{pmatrix}\] \[ds^2=(dx^1)^2-(dx^2)^2-(dx^3)^2-(dx^4)^2\] \[\overrightarrow{OM^2}=(dx^1)^2-(dx^2)^2-(dx^3)^2-(dx^4)^2\]

Le théorème de Pythagore n’a donc plus de sens dans un tel espace.

Soit alors le vecteur \(\overrightarrow{V}=(v^0,~v^1,~v^2,~v^3)\). On sait que \( v_{\alpha}=g_{\alpha\beta}~v^{\beta} \).

D’où : \[v_0=g_{0\beta}~v^{\beta}=g_{00}~v^0\quad;\quad v_1=g_{1\beta}~v^{\beta}=-v^1\]

En résumé : \[v_0=v^0\quad;\quad v_i=-v^i\qquad\text{ avec :}\quad i=1,~2,~3\]

Dans un espace ordinaire, on aurait \(v_i=v^i\).

Il existe dans ce nouvel espace trois vecteurs \(\overrightarrow{L}\ (\overrightarrow{L}\neq 0)\) tels que :

\[\begin{aligned} &L^2>0~:\quad(x^0)^2>\sum_{i}(x^i)^2 &&\text{Vecteur temporel} \\ &L^2<0~:\quad(x^0)^2<\sum_{i}(x^i)^2 &&\text{Vecteur spatial} \\ &L^2=0~:\quad(x^0)^2=\sum_{i}(x^i)^2 &&\text{Vecteur isotrope (ou lumière)}\end{aligned}\]

3. Espace temps de Minkowski

On considère un espace euclidien affine à quatre dimensions (trois spatiales et une temporelle). Tout point y est appelé événement : cette variété est appelée espace-temps de Minkowski. On suppose, en relativité restreinte, que l’on peut rapporter au moins un morceau de cet espace à des coordonnées galiléennes.

Les variables \([x,~y,~z]\) représentent les coordonnées dans un repère galiléen ordinaire auquel on associe un temps : toutes les horloges peuvent être mises à la même heure. Les coordonnées galiléennes d’un événement de l’espace-temps seront \([x,~y,~z,~t]\).

On peut changer de repère galiléen : \[M(x,~y,~z,~t)\quad\rightarrow\quad M'(x',~y',~z',~t')\]

mais la transformation devra être telle que : \[c^2~t^2-x^2-y^2-z^2=c^2~t'^2-x'^2-y'^2-z'^2\]

On pose : \[x^0=c~t\quad;\quad x^1=x\quad;\quad x^2=y\quad;\quad x^3=z\]

La signature est hyperbolique : \[s^2=(x^0)^2-(x^1)^2-(x^2)^2-(x^3)^2\]

3.1. La géométrie de l’espace-temps

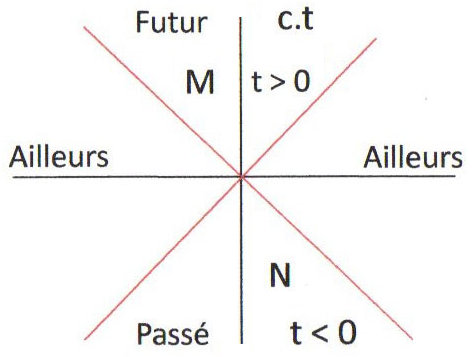Trois notions sont introduites : le passé, le futur et l’ailleurs d’un événement.

Par \(O\in E_4\), on fait passer la surface (cône de lumière) : \[c^2~t^2-x^2-y^2-z^2=0\]

Soit \(M\) un point du futur, l’événement se passant après \(O\) : \[c^2~t^2 > x^2 + y^2 + z^2\]

Examinons plusieurs possibilités :

1. Un courrier partant de \(O\) à l’instant \(t = 0\) arrive en \(M\) à l’instant \(t\) (il parcourt \(\sqrt{x^2+y^2+z^2}\)). Or, \(c^2~t^2>x^2+y^2+z^2\). Il faut donc que \(v<c\). \(M\) peut donc être informé de \(O\) : \(O\) est la cause, \(M\) en est l’effet.

   Futur de \(O\) : ensemble des événements sur lesquels \(O\) ne peut exercer d’influence.

2. \(N\) est un point du passé. Ce point peut être l’une des causes de \(O\).

3. Un point de l’ailleurs n’est jamais informé de \(O\) (il faudrait avoir \(v>c\)).

4. Les points situés exactement sur le cône sont les trajectoires des photons émis par \(O\).

3.2. La ligne d’univers d’une particule

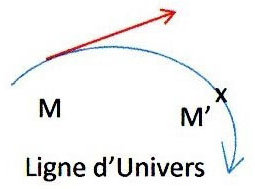La ligne d’univers est la trajectoire correspondant à l’ensemble des événements que vit une particule. On peut considérer également un vecteur tangent \(\vec{u}\) à cette trajectoire. Au repos par rapport à un repère, cette ligne d’univers est une droite.

En mouvement rectiligne uniforme, la ligne d’univers est encore une droite : \[x=v_x~t\quad;\quad y=v_y~t\quad;\quad z=v_z~t\quad;\quad t=t\]

On reconnaît l’équation paramétrique d’une droite à 4 dimensions : la ligne d’univers est quelque chose d’intrinsèque.

3.3. Remarque sur les vecteurs spatiaux et temporels

Deux vecteurs \(\overrightarrow{V}\) et \(\overrightarrow{W}\) sont orthogonaux quand \(\overrightarrow{V}\cdot\overrightarrow{W}=0\), soit \(v^{\alpha}~w_{\alpha}=0\) : \[v^0~w_0+v^1~w_1+v^2~w_2+v^3~w_3=0\] \[v^0~w_0-v^1~w_1-v^2~w_2-v^3~w_3=0\]

Deux vecteurs temporels ne peuvent être orthogonaux. En effet, considérons un repère tel que : \[\overrightarrow{V}(v^0,~0,~0,~0)\quad\text{et}\quad\overrightarrow{W}(w^0,~w^1,~w^2,~w^3)\] \[\overrightarrow{V}\cdot\overrightarrow{W}=0\quad\Rightarrow\quad v^0~w^0=0 \quad\Rightarrow\quad w^0=0\qquad\text{car :}\quad v^0\neq 0\]

Donc, si un vecteur \(\overrightarrow{V}\) est temporel, tous les vecteurs orthogonaux à \(\overrightarrow{V}\) sont spatiaux. Ils appartiennent à un trois-plans spatial. Ce trois-plans est dit espace associé au temps défini par le vecteur temporel. Par exemple, la salle de cours est un trois-plans orthogonal au vecteur temporel.