1. Le vecteur vitesse

Mesurons le vecteur \(\overrightarrow{\lambda}\) tangent à la ligne d’univers : \[x^{\alpha}=x^{\alpha}(s)\quad;\quad s=M_0M\] \[{\lambda}^\alpha=\frac{dx^{\alpha}}{ds}~~\text{ est un vecteur unitaire.}\]

En effet : \[dx^{\alpha}~dx_{\alpha}=g_{\alpha\beta}~dx^{\beta}~dx_{\beta}=ds^2\] \[{\lambda}^{\alpha}~{\lambda}_{\alpha}=\frac{dx^{\alpha}}{ds}~\frac{dx_{\alpha}}{ds}=\frac{ds^2}{ds^2}=1\]

Quel rapport avec la vitesse ordinaire dans le même repère galiléen ? \[{\lambda}^i=\frac{dx^i}{ds}=\frac{dx^i}{dt}~\frac{dt}{ds}=v^i\frac{dt}{ds}\quad;\quad i=1,~2,~3\] \[ds^2=c^2~dt^2-dx^2-dy^2-dz^2=c^2~dt^2-dl^2\] \[v^2=\frac{dl^2}{dt^2}=\frac{dx^2+dy^2+dz^2}{dt^2}\] \[ds^2=c^2~dt^2-v^2~dt^2\quad\Rightarrow\quad ds=c~\sqrt{1-\frac{v^2}{c^2}}~dt={\alpha}~c~dt\] \[\frac{dt}{ds}=\frac{1}{\alpha~c}\]

On obtient alors :

\[\begin{aligned} \lambda^i&=\frac{v^i}{\alpha~c}\quad;\quad i=1,~2,~3 \\ x^0&=c~t \\ \lambda^0&=\frac{dx^0}{ds}=\frac{dx^0}{dt}~\frac{dt}{ds}= c~\frac{1}{\alpha~c} \quad\Rightarrow\quad\lambda^0 = \frac{1}{\alpha}\end{aligned}\]

2. Le vecteur accélération

Par définition : \[\Gamma^{\alpha}=\frac{d\lambda^{\alpha}}{ds}\quad;\quad\alpha=1,~2,~3\]

On peut écrire :

\[\begin{aligned} &\lambda^\alpha~\Gamma^{\alpha}=\lambda^{\alpha}~\Big(\frac{d\lambda^{\alpha}}{ds}\Big)\\ &\lambda^{\alpha}~{\Gamma}^{\alpha}={\lambda}^{\alpha}~\frac{d \lambda^{\alpha}}{ds} =\frac{d}{ds}({\lambda}_{\alpha}~{\lambda}^{\alpha})- {\lambda}^{\alpha}~\frac{d\lambda_{\alpha}}{ds}\end{aligned}\]

D’où : \[\frac{d}{ds}({\lambda}_{\alpha}~{\lambda}^{\alpha})={\lambda}^{\alpha}~\frac{d \lambda^{\alpha}}{ds} +{\lambda}^{\alpha}~\frac{d\lambda_{\alpha}}{ds}\]

Or, on sait que :

\[\begin{aligned} &{\lambda}_{\alpha}~{d\lambda}^{\alpha}={\lambda}_{\alpha}~g^{\alpha \beta}~{d\lambda}_{\beta} \\ &{\lambda}^{\alpha}~{d\lambda}_{\alpha}=g^{\alpha \beta}~{d\lambda_{\alpha}}~{d\lambda}_{\beta}= g^{\beta \alpha}~{d\lambda_{\beta}}~{d\lambda}_{\alpha}\end{aligned}\]

Il s’ensuit que : \[\frac{d}{ds}({\lambda}_{\alpha}~{\lambda}^{\alpha})=2~\lambda_{\alpha}~\frac{d\lambda^{\alpha}}{ds} \qquad\text{et}\qquad \lambda_{\alpha}~\frac{d\lambda^{\alpha}}{ds}=\frac{1}{2}~\frac{d}{ds}({\lambda}_{\alpha}~{\lambda}^{\alpha})\]

Par suite : \[{\lambda}^{\alpha}~{\Gamma}^{\alpha}=\frac{1}{2}~\frac{d}{ds}({\lambda}_{\alpha}~{\lambda}^{\alpha})\qquad \text{car :}\quad{\lambda}_{\alpha}~{\lambda}^{\alpha}=1\quad\text{et}\quad\lambda\ \bot\ \Gamma\]

On a respectivement :

\[\begin{aligned} \Gamma^i&=\frac{d\lambda^i}{ds}~\frac{dt}{ds}=\frac{d}{dt}\Big(\frac{v^i}{\alpha~c}\Big)\Big(\frac{1}{\alpha c}\Big) \quad\Rightarrow\quad \Gamma^i=\frac{1}{\alpha~c^2}~\frac{d}{dt}\Big(\frac{v^i}{\alpha}\Big)\quad;\quad i=1,~2,~3 \\ \Gamma^0&=\frac{d\lambda^0}{ds}~\frac{dt}{ds}=\frac{d}{dt}\Big(\frac{1}{\alpha}\Big)\Big(\frac{1}{\alpha c}\Big) ~~~\quad\Rightarrow\quad\Gamma^0=\frac{1}{\alpha~c}~\frac{d}{dt}\Big(\frac{1}{\alpha}\Big)\end{aligned}\]

3. Application

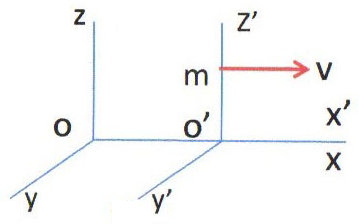Soit un repère galiléen à 3 dimensions et une particule \(M\) animée d’une vitesse \(\vec v\ //\ \vec{Ox}\) par rapport à ce repère. Attachons à \(M\) un repère galiléen propre : \(V_M\ /\ R'=0\)

3.1. Calcul de la vitesse

\[x=\frac{x'+v~t'}{\alpha}\quad;\quad y=y'\quad;\quad z=z'\quad;\quad t=\frac{t'+\cfrac{v~x'}{c^2}}{\alpha}\]

En différentiant : \[dx=\frac{dx'+v~dt}{\alpha}\quad;\quad dt=\frac{dt'+\cfrac{v~dx'}{c^2}}{\alpha} \quad\Rightarrow\quad \frac{dt}{dt'}=\frac{1+\cfrac{v}{c^2}~\cfrac{dx}{dt}}{\alpha}\]

D’où les dérivées :

\[\begin{aligned} \frac{dx}{dt}&=\frac{dx'+vdt}{dt'+\cfrac{v}{c^2}~dx'}=\frac{\cfrac{dx'}{dt'}+v}{dt'+\cfrac{v}{c^2}~\cfrac{dx'}{dt'}} \\ \frac{dy}{dt}&=\frac{dy'}{dt'}~\frac{dt'}{dt}\\ \frac{dz}{dt}&=\frac{dz'}{dt'}~\frac{dt'}{dt}\end{aligned}\]

3.2. Calcul de l’accélération

Nous posons, pour alléger l’écriture de la formule qui va suivre : \[\Delta=1+\frac{v}{c^2}~\frac{dx'}{dt'}\] \[\Gamma_x=\frac{d^2 x}{dt^2}\quad;\quad\Gamma_x'=\frac{d^2 x'}{dt'^2}\]

On peut alors écrire : \[\Gamma_x=\frac{\Gamma_x'~\Delta-\cfrac{v}{c^2}~\Gamma_{x'}~\Big(\cfrac{dx'}{dt'}+v\Big)}{\Delta^2}~\frac{\alpha}{\Delta}\]

À l’instant \(t\), la vitesse de \(M\) dans son repère propre est nulle : \[\frac{dx'}{dt'}=0\]

Tous calculs faits : \[\Gamma_x = \Gamma_x'~\Big(1-\frac{v^2}{c^2}\Big)~\alpha = \alpha^3~\Gamma_x'\]

En mécanique classique \(\Gamma_x = \Gamma_x'\), donc le principe fondamental de la dynamique est en cause. On obtiendrait également : \[\Gamma_y=\alpha^2~\Gamma_y'\quad;\quad\Gamma_z=\alpha^2~\Gamma_z'\]

La notion de masse est également remise en cause : on associe donc à \(\Gamma_x\) une masse longitudinale \(m_l\)  et également à \(\Gamma_y\) et à \(\Gamma_z\), composantes de l’accélération transversale, une masse transversale \(m_t\).