1. Équilibre thermique

Considérons un système thermodynamique, par exemple un mélange gazeux de masse et composition chimique déterminées. On suppose qu’il ne s’y produit aucune réaction chimique.

La pression P et le volume V du gaz peuvent être modifiés indépendamment et volontairement. Il s’agit de variables indépendantes dont la connaissance suffit à déterminer ce que nous appelons l’état du système.

Dans une pile, la connaissance de deux coordonnées (la f.é.m. E et la charge Q) suffira, dans certaines conditions, à définir l’état du système.

Faisons l’hypothèse de systèmes à deux variables indépendantes notées x et y. Si leurs valeurs sont définies et ne changent pas tant que le milieu extérieur reste invariable, nous dirons que le système est en équilibre.

Considérons maintenant deux systèmes A et B, pas nécessairement de même nature, définis respectivement par les coordonnées [x, y] et [x’, y’]. Ces deux systèmes sont séparés par une cloison indéformable.

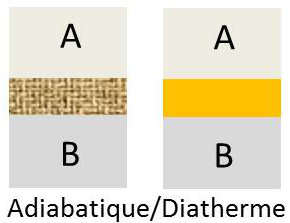
Deux cas peuvent se présenter,suivant le type de cloison :

1. Tout état d’équilibre [x, y] du système A peut coexister avec tout état d’équilibre [x’, y’] du système B.

   La cloison C est alors dite adiabatique (exemple : couche de liège).

2. Lors de la mise en contact par l’intermédiaire de la cloison C des systèmes initialement en équilibre, chaque système évolue jusqu’à ce que l’ensemble AB atteigne un nouvel équilibre.

   La cloison C est alors dite diatherme, et l’équilibre vers lequel tend l’ensemble AB est un équilibre thermique. Un bon exemple de cloison diatherme est fourni par une mince plaque de cuivre.

Remarque

Deux systèmes mis depuis longtemps en communication par une cloison diatherme sont donc en équilibre thermique. Leur état est caractérisé par un ensemble de coordonnées qui ne peuvent prendre indépendamment des valeurs quelconques.

2. Principe zéro de la thermodynamique

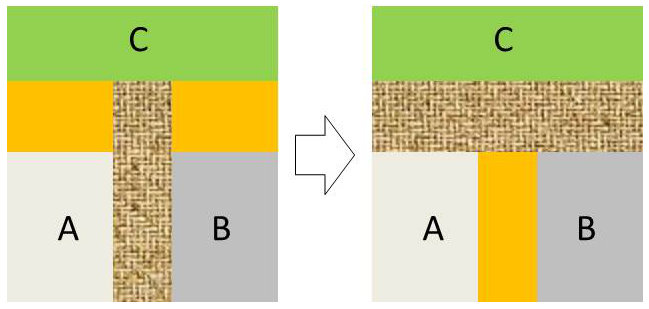Supposons que les systèmes A et B, séparés par une cloison adiabatique, soient mis en contact séparément avec un système C par des cloisons diathermes.

L’équilibre atteint, séparons C par une cloison adiabatique et mettons en contact A et B par une cloison diatherme.

L’expérience montre que A et B n’évoluent pas : ils sont donc déjà en équilibre thermodynamique.

Le principe zéro de la thermodynamique s’énonce ainsi :

Deux systèmes en équilibre thermique avec un troisième sont en équilibre thermique entre eux.

3. Concept de température

Représentons les états d’équilibre du système A dans le diagramme [\(x,y\)] et ceux du système B dans le diagramme [x’, y’].

3.1. Isothermes

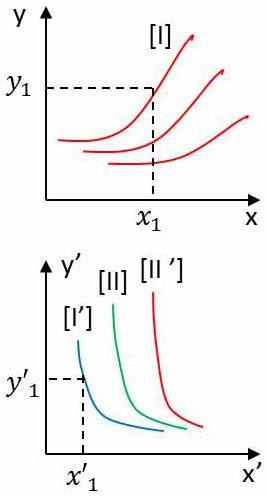Considérons tous les états d’équilibre de A, qui se trouvent en équilibre thermique avec un état déterminé [\(x'_1,~y'_1\)] de B. Les points représentatifs de ces états se répartissent sur une courbe [I] supposée continue pour simplifier et désignée isotherme de A.

Prenons maintenant l’un des états de A et cherchons tous les états de B qui se trouvent à l’équilibre thermique avec cet état de A. Ces états de B se répartissent sur une courbe [I’] qui passe évidemment par le point \([x'_1,~y'_1]\) et donc l’isotherme de B.

En application du principe zéro de la thermodynamique :

1. Tous les états de A situés sur l’isotherme [I] sont en équilibre entre eux (étant déjà équilibre thermique avec le même état \([x'_1,~y'_1]\) de B).

2. De même, tous les états de B situés sur l’isotherme [I’] sont en équilibre thermique entre eux (raisonnement dual du précédent).

3. Un état quelconque de A situé sur l’isotherme [I] est en équilibre thermique avec un état quelconque de B situé sur l’isotherme [I’].

Les isothermes [I] et [I’] sont des isothermes correspondantes de A et B.

Recommençons le tout à partir d’un état initial quelconque de B. Nous obtenons deux nouveaux isothermes [II] et [II’] (si l’état de B a été pris en dehors de l’isotherme [I’]).

Recommençons pour une infinité d’états initiaux de B. Nous obtenons deux réseaux d’isothermes deux à deux correspondants (chacun des réseaux comportant une simple infinité de courbes) d’où la loi :

La condition nécessaire et suffisante pour que le système A et le système B soient en équilibre thermique est que les points représentatifs de A et B soient sur une paire d’isothermes correspondants.

Notons enfin que l’application du principe zéro permet d’affirmer que le réseau d’isothermes de A (par exemple) est indépendant du système auxiliaire B arbitrairement choisi pour le tracer.

3.2. Concept

L’application du principe zéro permet dès lors de tracer pour un ensemble de systèmes quelconques des réseaux d’isothermes se correspondant n à n.

Il apparaît alors que tous les états de tous les systèmes pris sur des isothermes correspondants ont une propriété commune à savoir la propriété d’être en équilibre thermique entre eux, et de ne pas être en équilibre thermique avec un état quelconque de l’un des systèmes considérés qui n’appartiennent pas à leur famille.

Cette propriété commune est celle que nous désignons sous le nom de température .

Cette notion même de température, propriété intrinsèque d’un système en équilibre interne, et indépendante de toute mise en relation de ce système avec d’autres, est essentiellement liée à la validité du principe zéro.

4. Repérage de température

Il est permis d’affecter à chaque isotherme du système A un nombre qui sera le même pour les isothermes correspondants de tous les autres systèmes considérés.

À chaque état d’un système quelconque sera ainsi affectée une température qui sera la même d’ailleurs pour tous les états appartenant au même isotherme. La température constitue maintenant une nouvelle donnée thermodynamique.

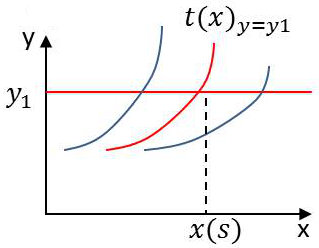
Dans ce but, nous choisissons un système A nommé thermomètre et dépendant de deux coordonnées [x, y]. Nous fixerons l’une d’elles, par exemple y à la valeur \(y_1\). Puis nous amènerons le thermomètre à l’équilibre thermique avec le système dont nous voulons repérer la température. La variable x évolue et se fixe à la valeur x(s).

Faisant choix d’une fonction commode t(x), nous désignerons par température du système (c’est aussi celle du thermomètre) ce nombre t(x).

La grandeur physique dont la mesure est x est nommée grandeur thermométrique.

La fonction t(x) est la fonction thermométrique.

L’ensemble des t(x) obtenus en mettant successivement en équilibre thermométrique avec toutes sortes de systèmes constitue l’échelle du thermomètre considéré, y restant constant et égal à \(y_1\).

À titre d’exemple, on peut choisir pour grandeur thermométrique :

• la pression d’une masse déterminée d’un gaz donné maintenu à volume constant ;

• le volume d’une masse déterminée d’un gaz donné maintenu à pression constante ;

• la résistance d’un fil de platine donné maintenu à pression et tension constantes ;

• la f.é.m. d’un thermocouple donné maintenu à pression et tension constantes ;

• la longueur d’une colonne de liquide enfermé dans un capillaire ;

• etc.

Le but à atteindre est évidemment de définir une échelle thermométrique commode et universellement acceptée.

Les idées à ce sujet ont évolué et nous commencerons par exposer la méthode qui avait été primitivement adoptée, ceci pour nous permettre de mieux comprendre les critiques qui ont été formulées à son encontre et qui ont conduit en 1954 à son remaniement.