1. Avant-propos (personnel)

Le contenu de ce chapitre n’est pas fondamental pour la suite de ce cours. Il ne faut y voir que l’aspect documentaire, historique au sens scientifique du terme. Car ses conclusions sont devenues des évidences à notre époque. Cependant, il est bon d’avoir présentes à l’esprit les démarches et les méthodes expérimentales de ces gens que l’on n’appelait pas des chercheurs, jadis, et qui pourtant en furent et des vrais.

Pour ajouter un brin d’humour à cette parenthèse, je me hasarderai à cette citation, venue du comique Coluche qui disait :

Celui qui, partant de rien, est arrivé à pas grand chose a fait un pas énorme.

Notre manuscrit date des années 1960. Les choses ont nettement évolué depuis un demi-siècle en matière de méthodes et de précision des mesures mais, au nom du respect pour un certain passé scientifique, le contenu de ce chapitre a été conservé pratiquement en l’état.

2. Première échelle à deux points fixes (Avogadro)

La première méthode, dite à deux points fixes, adoptée avant 1954, postulait une fonction thermométrique de la forme : \(y=ax+b\).

Les constantes \(a\) et \(b\) sont déterminées en fixant la température de deux points fondamentaux : le point glace et le point vapeur, c’est-à-dire :

• Eau saturée d’air en équilibre avec la glace à la pression atmosphérique normale : 0 °

• Vapeur d’eau en équilibre avec l’eau pure à la pression atmosphérique normale : 100 °

Soient \(x_g\) et \(x_v\) les valeurs que prend \(x\) quand on place successivement le thermomètre à l’équilibre thermique avec les systèmes considérés (glace fondante et vapeur).

Écrivons les deux relations :

\[\begin{aligned} &t(x_g)=a~x_g+b=0\\ &t(x_v)=a~x_v+b=100\end{aligned}\]

Il vient : \[a=\frac{100}{x_v-x_g}\quad;\quad b=-\frac{100~x_g}{x_v-x_g}\]

La fonction thermométrique est donc entièrement définie et s’écrit : \[t(x)=100~\frac{x-x_g}{x_v-x_g}\]

Ainsi est définie une échelle centésimale de températures, la formule s’appliquant à différents types de thermomètres (variable \(x\) ) :

• Thermomètre à gaz à pression constante\([v,v_v,v_g]\)

• Thermomètre à gaz à volume constant\([p,p_p,p_g]\)

• Thermocouple\([E,E_v,E_g]\)

• Thermomètre à résistance de platine\([R,R_v,R_g]\)

• Thermomètre à liquide\([l,l_v,l_g]\)

2.1. Comparaison des différentes échelles

Considérons un système S de caractéristiques invariables. Repérons sa température en amenant à l’équilibre thermique avec S un thermomètre quelconque.

La température obtenue dépend du thermomètre choisi. Nous dirons donc que les différentes échelles ne coïncident pas (en fait, elles ne coïncident qu’aux points 0 et 100) :

• Thermomètre à hydrogène à volume constant :60 °

• Thermomètre à air à volume constant :59,990 °

• Thermomètre à résistance de platine :60,360 °

• Thermomètre à mercure :60,086°

• Thermocouple platine-platine rhodié :60,293 °

On a supposé les températures obtenues en utilisant pour tous ces thermomètres la même fonction thermométrique linéaire : \[t(x)=100~\frac{x-x_g}{x_v-x_g}\]

On remarque que les deux thermomètres à gaz donnent des indications très voisines. Ce qui conduira à considérer de plus près les échelles définies par ces types de thermomètres.

2.2. Vers la limite « pression nulle »

Un thermomètre à gaz peut être utilisé soit à volume constant, soit à pression constante.

On peut à priori choisir pour le remplissage un gaz quelconque, à une pression initiale quelconque. L’échelle définie dépend du mode de fonctionnement (volume constant ou pression constante), du gaz choisi et de la pression de remplissage.

L’expérience montre que tous les thermomètres à gaz, à pression ou à volume constant, définissent la même échelle de température lorsque cette pression devient assez faible.

Considérons un thermomètre à hydrogène à volume constant. Amenons-le à l’équilibre thermique avec la glace fondante et emplissons-le d’hydrogène à la pression p=100 cm Hg.

Fermons le réservoir et amenons le thermomètre à l’équilibre thermique avec le point vapeur. La pression devient \(p_v\).

Amenons le thermomètre à l’équilibre thermique avec le système S de caractéristiques invariables et notons la pression \(p\) obtenue.

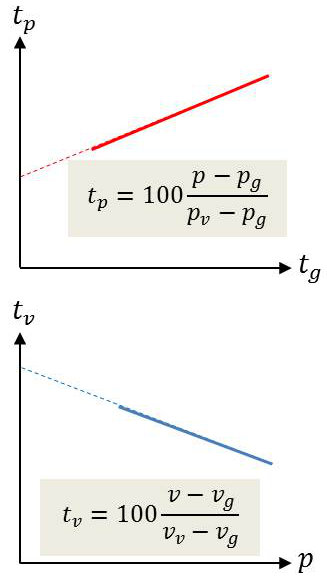Calculons la température ainsi définie : \[t_p=100~\frac{p-p_g}{p_v-p_g}\qquad;\qquad p_g=100~cm~Hg\]

Retirons du gaz de façon que la pression devienne 10 cm Hg au point glace.

Notons les nouvelles valeurs \(p_v\) (vapeur) et \(p\) et calculons la nouvelle température : \[t_p=100~\frac{p-p_g}{p_v-p_g}\qquad;\qquad p_g=10~cm~Hg\]

Recommençons pour des pressions initiales de plus en plus faibles et portons sur un diagramme \(t_p\) en fonction de la pression initiale \(p_g\).

Extrapolons jusqu’à l’axe des pressions nulles la courbe obtenue.

L’ordonnée du point d’intersection est : \[t=\lim_{p_g\rightarrow 0}\Big(100~\frac{p-p_g}{p_v-p_g}\Big)\]

Reprenons les mêmes mesures avec un thermomètre à hydrogène à pression constante \(p\).

Réglant à la valeur 100 cm Hg, nous obtenons une température du système S : \[p=100~cm~Hg\quad;\quad t_v = 100~\frac{v-v_g}{v_v-v_g}\]

Abaissons \(p\) à 10 cm Hg en retirant du gaz, et calculons à partir des nouvelles valeurs obtenues pour \([v_g,v_v,v]\) la nouvelle température de S : \[p=10~cm~Hg\quad;\quad t_v = 100~\frac{v-v_g}{v_v-v_g}\]

Recommençons pour des pressions de plus en plus faibles, et portons sur un diagramme la valeur obtenue pour \(t_v\)en fonction de la fonction de remplissage \(p\).

Extrapolons la courbe jusqu’à l’axe des pressions nulles.

L’ordonnée \(t\) du point d’intersection est : \[t=\lim_{p\rightarrow 0}\Big(100~\frac{v-v_g}{v_v-p_g}\Big)\]

soit la même que précédemment.

Bien plus, si nous reprenons l’expérience avec des gaz de remplissage différents, nous arrivons toujours à la même limite \(t\). Nous définirons alors la température du système S par la relation : \[\lim_{p_g\rightarrow 0} t_p = \lim_{p\rightarrow 0} t_v = t\]

L’échelle des températures \(t\) ainsi définies prend donc un caractère universel. Cette échelle, connue sous le nom d’échelles d’Avogadro, a été universellement utilisée jusqu’en 1954.

Elle était définie, soit à partir d’un thermomètre à gaz quelconque à volume constant, par la relation : \[t=\text{limite}_{p_g\rightarrow 0}\Big(100~\frac{p-p_g}{p_v-p_g}\Big)\]

soit à partir d’un thermomètre à gaz quelconque à pression constante par la relation : \[t=\lim_{p\rightarrow 0}\Big(100~\frac{v-v_g}{v_v-p_g}\Big)\]

3. Température absolue

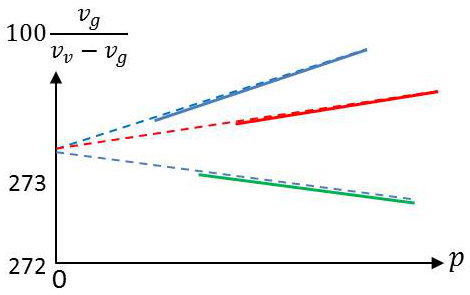Reprenons les expériences du paragraphe précédent et portons sur un même diagramme la valeur des quantités : \[100~\frac{p_g}{p_v-p_g}\quad\text{ou bien}\quad 100~\frac{v_g}{v_v-v_g}\]

suivant la fonction de remplissage.

En fonction la nature du gaz de remplissage, nous obtenons diverses courbes que nous pouvons extrapoler jusqu’à \(p_g=0\) ou \(p=0\). Toutes ces courbes viennent converger sur l’axe des pressions nulles en un point d’ordonnée \(T_g\).

Ainsi apparaît une constante universelle \(T_g\) qui peut être définie par l’une ou l’autre des relations : \[T_g=\lim_{p_g\rightarrow 0}\Big(100~\frac{p_g}{p_v-p_g}\Big) \qquad\text{ou}\qquad T_g=\lim_{p\rightarrow 0}\Big(100~\frac{v_g}{v_v-p_g}\Big)\]

et ceci, sans spécifier le gaz utilisé.

Les diverses valeurs obtenues pour \(T_g\) se répartissent entre 273,13 ° et 273,17 °. La moyenne des déterminations expérimentales les plus précises de \(T_g\) fournit une valeur voisine de 273,15 °.

Une nouvelle échelle

Introduisons alors une nouvelle échelle de température : \[T~=~t~+~T_g\]

qui se déduit de l’échelle d’Avogadro par simple déplacement de l’origine.

Cette échelle de températures, dite échelle absolue, était ainsi définie jusqu’en 1954.

On ne saurait imaginer une température négative dans cette échelle absolue. La température T d’un système peut en effet être directement définie par la relation : \[\frac{T}{100}=\lim_{p\rightarrow 0}~\frac{v-v_g}{v_v-p_g}+\lim_{p\rightarrow 0}~\frac{v_g}{v_v-p_g} = \lim_{p\rightarrow 0}~\frac{v}{v_v-p_g}\]

Et l’on ne saurait concevoir que le volume du gaz thermométrique devienne négatif. Le point zéro de cette échelle (zéro absolu) apparaît donc comme une limite infranchissable.

Nous verrons dans la suite du cours que l’échelle absolue coïncide avec une échelle introduite de façon logique par la thermodynamique, que nous désignerons sous le nom d’échelle thermodynamique en kelvins (symbole K).

Dores et déjà, nous exprimerons les températures absolues en kelvins.

4. Méthode utilisée depuis 1954. Échelle à un seul point fixe

4.1. Inconvénients de l’échelle à deux points fixes

L’échelle d’Avogadro était définie en attribuant les températures 0 et 100 à deux points fixes fondamentaux, l’échelle absolue s’en déduisant par une translation du zéro égale à \(T_g\). D’où une difficulté du fait que la valeur de \(T_g\) n’est pas connue de manière rigoureuse.

Or, c’est la température qui s’identifiera avec la température thermodynamique à la signification physique intrinsèque. L’incertitude sur \(T_g\) étant de l’ordre de 0,04 °, il peut en résulter une incertitude identique sur la température absolue d’un système quelconque. Ceci ne présente pas d’inconvénients que pour les basses températures obtenues par les moyens modernes.

Supposons par exemple qu’une table de constantes indique que température d’ébullition de l’hélium à la pression atmosphérique normale est –268,93 °, ceci sans que soit spécifiée la valeur adoptée pour \(T_g\) par les expérimentateurs qui ont fait la mesure. L’utilisateur en déduira que la température d’ébullition de l’hélium est comprise entre 4,20 et 4,24 K, soit une incertitude de près de 1 %.

Pour éviter cet inconvénient, depuis 1954, l’échelle absolue est directement définie à partir d’un seul point fixe auquel est attribuée une température absolue choisie une fois pour toutes en tant que constante universelle.

4.2. Échelle à un point fixe

Le thermomètre utilisé pour définir l’échelle est le thermomètre à gaz, la fonction thermométrique est maintenant de la forme : \[T~=~a~x\]

Le système choisi pour définir le point fixe est le système (eau pure - vapeur d’eau - glace) ou encore le point triple (liquide - solide - vapeur) de température 0,01 ° dans l’échelle d’Avogadro.

Ce système est en effet plus aisément reproductible que le point glace adopté auparavant. Il était en effet difficile de maintenir l’eau saturée d’air au voisinage du thermomètre, la fusion de la gaine de glace qui l’entoure produisant de l’eau pure.

On attribue une fois pour toutes à ce système la température absolue \(T=-273,16~K\).

Cette température est définie à partir d’un thermomètre à gaz à volume constant par la relation : \[T=273,16~\lim_{p_t\rightarrow 0}~\Big(\frac{p}{p_t}\Big) \qquad p_t~:~\text{pression au point triple}\]

ou à partir d’un thermomètre à gaz à pression constante par la relation : \[T=273,16~\lim_{p\rightarrow 0}~\Big(\frac{v}{v_t}\Big)\]

4.2.1. Échelle Celsius

L’échelle d’Avogadro est alors remplacée par l’échelle Celsius , déduite de la nouvelle échelle absolue par déplacement de l’origine de l’origine choisie une fois pour toutes, c’est-à-dire: \[t/^\circ C=T/K-273,15\]

Dans cette nouvelle échelle :

• la température du point triple de l’eau est exactement égale à : 0,01 °C,

• la température du point glace est très sensiblement égale à 0,00 °C,

• la température du point vapeur est très sensiblement égale à 100,00 °C.

L’échelle Celsius coïncide pratiquement avec l’échelle Avogadro et nous y exprimons les températures aussi bien en degrés centigrades qu’en degrés Celsius.

4.2.2. Points fixes. Échelle internationale de températures

La détermination d’une température au thermomètre à gaz est une opération extrêmement longue et délicate. Il ne saurait être question de reproduire cette opération chaque fois qu’il est nécessaire d’étalonner une série de thermomètres commerciaux.

On a donc convenu de définir une échelle internationale de température, définie à partir de thermomètres étalons d’usage plus commode que le thermomètre à gaz. Cette échelle internationale a été établie de façon à ne présenter que des différences très faibles et généralement négligeables avec l’échelle Celsius.

Elle doit être considérée comme une représentation commode de l’échelle Celsius, cette dernière restant l’échelle fondamentale (au même titre que l’échelle absolue dont elle se traduit par une translation parfaitement définie).

Pour établir l’échelle internationale, on a au préalable déterminé au thermomètre à gaz, dans l’échelle absolue, la température d’un certain nombre de systèmes aisément reproductibles, les températures obtenues constituent l’ensemble des points fixes qui suivent.

Ces points se répartissent en :

• point fixe fondamental ou point triple de l’eau : 273,16 K et 0,01 °C ;

• points fixes de base (à la pression atmosphérique) ;

• points fixes secondaires (également à la pression atmosphérique).

On notera les abréviations : eb (ébullition), eq (équilibre), fus (pour fusion)

Points fixes de base \[\begin{matrix} &O_2(eb)& &90,18~K& &182,97~^\circ C\\ &glace-eau(eq)& &273,15~K& &0,00~^\circ C\\ &eau-vapeur(eq)& &373,15~K& &100,00~^\circ C\\ &S(eb)& &717,75~K& &444,60~^\circ C\\ &Sb(fus)& &903,65~K& &630,50~^\circ C\\ &Ag(fus)& &1233,95~K& &960,80~^\circ C\\ &Au(fus)& &1336,15~K& &1063,00~^\circ C \end{matrix}\]

Points secondaires (quelques points) \[\begin{matrix} &He(eb)& &4,22~K& &-268,93~^\circ C\\ &H_2(eb)& &20,37~K& &-252,18~^\circ C\\ &Zn(fus)& &692,65~K& &419,50~^\circ C \end{matrix}\]

L’échelle internationale a été établie de façon à coïncider exactement avec l’échelle Celsius pour les points fixes de base. Parmi ces points fixes, deux étaient les points fixes fondamentaux dans l’ancienne échelle (Avogadro).

Dans l’échelle Celsius maintenant adoptée, le point fixe fondamental est le point triple de l’eau et ne figure pas en toute rigueur parmi les points où l’échelle internationale a été amenée à coïncider exactement avec l’échelle du thermomètre à gaz.

Mais ce point triple est tellement proche du point glace que l’on peut considérer que l’échelle internationale coïncide avec l’échelle Celsius non seulement pour les points fixes de base mais aussi le point fondamental.

Pour assurer la coïncidence aux points fixes de base, on a partagé en trois parties l’intervalle de température séparant l’ébullition de l’oxygène de la fusion de l’or, et défini pour chacune de ces trois parties une échelle thermométrique internationale, de la façon suivante :

1. De 0 à 660 °C, le thermomètre choisi est le thermomètre à résistance de platine (fil de diamètre compris entre 0,05 et 0,2 mm), la température internationale étant définie par : \[R_t=R_0~(1+A~t+B~t^2)\]

   \(R_0,~A,~B\) sont déterminés pour faire coïncider l’échelle avec l’échelle Celsius aux points fixes 0 °, 100 ° et 444,60 °.

2. De –190 à 0 °C, même thermomètre que précédemment, la température internationale étant définie par : \[R_t=R_0~[1+A~t+B~t^2+C~t^3~(t-100)]\]

   \(C\) est choisi pour faire coïncider l’échelle avec l’échelle Celsius au point –182,97 °C.

3. De 660 à 1063 °C, le thermomètre choisi est le thermomètre à diamètre des fils compris entre 0,35 et 0,65 mm, avec soudure froide à 0 °C, la température internationale étant définie par : \[E_t=a+b~t+c~t^2\]

   \(a,~b,~c\) étant déterminés pour que l’échelle coïncide avec l’échelle Celsius aux points 630,50, 960,8 et 1063,0 °C.

On a étendu récemment l’emploi du thermomètre à résistance de platine jusqu’à –254 °C. La formule thermométrique est beaucoup plus compliquée.

Enfin, aux températures supérieures à 1063 °C, un thermomètre naturel se présente : c’est le pyromètre optique mesurant la luminance du corps noir dans une longueur d’onde quelconque. De cette luminance peut être directement déduite, par la formule de Planck que nous établirons plus tard, la température thermodynamique, qui coïncide, comme nous l’avons déjà signalé, avec la température absolue.