1. Structure moléculaire d’un gaz

Une masse gazeuse contenue dans une enceinte est constituée d’un ensemble de molécules dont les dimensions, aux températures et pressions usuelles, sont très petites devant leurs distances mutuelles.

Ces molécules sont animées de vitesses de translation très grandes et s’entrechoquent constamment, de telle sorte que leurs parcours, pratiquement rectilignes entre deux chocs, dévie brutalement à chaque choc moléculaire ou à chaque choc de la molécule contre la paroi de l’enceinte et constitue une ligne brisée à éléments sensiblement rectilignes.

Outre ce mouvement de translation, chaque molécule est à priori susceptible de déformations internes et de rotation sur elle-même. Enfin, les molécules peuvent être toutes de même nature chimique (gaz pur) ou de natures différentes (mélanges gazeux).

2. Loi de répartition des vitesses à l’équilibre (Maxwell)

Nous considérons un gaz pur formé par l’ensemble de \(n\) molécules identiques enfermées dans une enceinte diatherme indéformable, elle-même en contact thermique avec un thermostat de température \(T\).

Cette masse gazeuse constitue un système thermodynamique que nous pouvons supposer avoir constitué à l’instant \(t\) en plaçant les \(n\) molécules en divers points à l’intérieur de l’enceinte et en les abandonnant toutes avec une vitesse initiale commune \(\vec{v}\).

Ces molécules se précipitent sur les parois de l’enceinte, y rebondissent suivant des directions variées, viennent heurter une autre paroi, se heurtent éventuellement entre elles ; au bout d’un laps de temps assez court, nous obtenons un désordre total dans les positions et les vitesses des molécules.

Parallèlement et suivant un point de vue macroscopique, nous reconnaissons que le gaz s’est mis à l’état d’équilibre thermodynamique et notamment à l’équilibre thermique avec l’enceinte de température \(T\). Cet équilibre n’est pas un équilibre statique, qui serait caractérisé par l’immobilité de tous les éléments, mais un équilibre statistique caractérisé par l’invariabilité au cours du temps de la répartition des positions et des vitesses moléculaires.

Précisons un peu cet équilibre statistique :

Nous supposons tout d’abord que la densité moléculaire est la même en tout point de l’enceinte. En d’autres termes, si nous partageons l’enceinte en éléments de volumes égaux \(dv\), très petits devant le volume total, mais cependant en nombre bien plus faible que le nombre total des molécules, chacun de ces éléments de volume contient très sensiblement à chaque instant le même nombre de molécules.

Nous pouvons exprimer ceci en disant que la probabilité pour qu’une molécule déterminée se trouve à l’instant \(t\) à l’intérieur d’un certain volume \(dv\) entourant le point de cordonnées \((x,~y,~z\) est égale à \(k~dv\), \(k\) étant une constante indépendante de \(x,~y,~z ,~t\) si le gaz est en équilibre.

Nous supposons en outre que dans chaque élément de volume, les molécules possèdent des vitesses dont les directions sont réparties uniformément dans tous les sens (isotropie de la distribution des vitesses) et dont les grandeurs sont elles-mêmes distribuées suivant une loi indépendante de la position de l’élément choisi. C’est en cela que consiste l’homogénéité de la distribution des vitesses.

On pourrait supposer à priori que la loi de la répartition des vitesses est constamment modifiée par les chocs moléculaires ; mais on peut démontrer, ainsi que l’a fait Maxwell que, lorsque l’équilibre thermique a été atteint, la loi suivant laquelle sont distribuées les grandeurs des vitesses n’est plus modifiée par les chocs intermoléculaires, ni par les chocs molécules – parois.

En d’autres termes, la position et la vitesse d’une molécule donnée changent constamment, mais la répartition des positions et des vitesses des molécules reste la même tant que dure l’équilibre thermique : c’est en cela que consiste l’équilibre statistique.

Cherchons alors comment nous pouvons déduire de ces hypothèses la loi de répartition des vitesses. Nous pouvons rapporter ces vitesses à trois axes de coordonnées rectangulaires le long desquels nous reporterons les trois composantes \([v_x^i,~v_y^i,~v_z^i]\) de la \(i^{\text{ème}}\) molécule dont le vecteur se trouve ainsi représenté par un point dans l’espace des vitesses.

L’ensemble des \(n\) points relatifs à l’ensemble des molécules représente complètement la distribution des vitesses moléculaires à un instant donné.

Soit \(F(u)~du\) la probabilité pour qu’une molécule donnée ait une composante de vitesse \(v_x\) comprise entre \(u\) et \(u+du\). L’isotropie de la distribution des molécules permettrait d’écrire les mêmes relations avec les autres composantes.

Nous en déduisons que la probabilité pour que le point représentatif \((v_x,~v_y,~v_z)\) soit compris dans l’élément de volume \(d\tau=du~dv~dw\) limité dans l’espace des vitesses par le plan de coordonnées \([u,u+du~;~v,v+dv~;~w,w+dw]\) est (hypothèse supplémentaire des probabilités indépendantes) : \[P(u,~v,~w)~d\tau=F(u)~F(v)~F(w)~du~dv~dw\]

Mais l’isotropie de distribution des vitesses exige que cette probabilité reste invariable pour une rotation quelconque autour de son origine du système d’axes de coordonnées, ce qui implique qu’elle ne dépende que de la grandeur de la vitesse résultante ou, si l’on veut, du carré de cette vitesse, de sorte que l’on peut écrire : \[F(u)~F(v)~F(w)=f(u^2+v^2+w^2)\]

On pense immédiatement à la fonction exponentielle pour répondre à cette condition de sorte que l’on pourra poser : \[f(u^2+v^2+w^2)=A~\exp\{-b~(u^2+v^2+w^2)\}\qquad\quad b~>~0\]

Cette contrainte sur la constante de l’exposant permet d’éviter une absurdité : celle d’une probabilité infinie de rencontrer une vitesse infinie.

On a donc : \[P(u,~v,~w)~d\tau=A~\exp\{-b~(u^2+v^2+w^2)\}~du~dv~dw\]

De plus, la valeur de la probabilité étendue à tout l’espace devant être égale à 1, la condition suivante doit être vérifiée : \[\iiint P(u,~v,~w)~d\tau~=~\int\limits_{-\infty}^{+\infty}\int\limits_{-\infty}^{+\infty}\int\limits_{-\infty}^{+\infty}A~\exp\{-b~(u^2+v^2+w^2)\}~du~dv~dw=1\]

Le calcul de l’intégrale est classique et conduit à la valeur : \[A=\Big(\frac{b}{\pi}\Big)^{3/2}\]

Comme on a coutume de poser \(b = h~m\), \(m\) étant la masse de la molécule : \[P(u,~v,~w)~du~dv~dw~=~\Big(\frac{b}{\pi}\Big)^{3/2}\exp\{-h~m~(u^2+v^2+w^2)\}~du~dv~dw\]

C’est la loi de Maxwell de répartition des vitesses à l’équilibre.

Cherchons la probabilité pour qu’une molécule ait une vitesse comprise entre \(c\) et \(c + dc\), l’orientation de cette vitesse étant quelconque.

Il faut procéder à une intégration du second membre entre les sphères de rayon \(c\) et \(c + dc\), soit, si \(n\) est le nombre total de molécules dans l’enceinte, une fraction \(dn\) ayant cette vitesse. \[dn=4~n~\sqrt{\frac{h^3~m^3}{\pi}}~\exp(-h~m~c^2)~c^4~dc\]

Car on a : \[dn=n~\frac{dV}{dr}=n~\frac{d}{dr}~\Big(\frac{4}{3}~\pi~r^3\Big)\qquad r\approx c\]

Nous pouvons en déduire une vitesse quadratique moyenne des molécules : \[C^2=\overline{c^2}=\frac{1}{n}\int_0^{\infty}c^2~dn=\sqrt{\frac{h^3~m^3}{\pi}}~\int_0^{\infty}\exp(-h~m~c^2)~c^4~dc=\frac{3}{2~h~m}\]

Nous pourrions enfin chercher la vitesse la plus probable \(c_0\). C’est la vitesse qui rend maximal le coefficient de \(dc\) dans l’expression de \(dc\), c’est-à-dire qui rend maximale l’expression de \(c^2\exp(-h.m.c^2)\) dont la dérivée par rapport à \(c\) est : \[(2~c-2~h~m~c^3)~\exp(-h~m~c^2)\]

C’est-à-dire : \[c_0=\frac{1}{\sqrt{h~m}}=C~\sqrt{\frac{2}{3}}\]

En définitive, nous voyons que les vitesses moléculaires sont réparties suivant une loi de Gauss, uniformément dans toutes les directions, et que l’énergie cinétique totale de translation des molécules est : \[E_c=\frac{1}{2}~m~c^2=n~\frac{m}{2}~\overline{c^2}=\frac{3~n}{4~h}\]

2.1. Modèle microscopique théorique du gaz parfait

Le gaz est considéré comme formé de molécules de dimensions infiniment petites et n’exerçant entre elles aucune force d’attraction ou de répulsion à distance. Cette hypothèse permet que le gaz satisfasse à la loi de Joule.

Nous aurons l’occasion de voir que l’invariance de température exige notamment l’invariance de l’énergie cinétique totale de translation des molécules. Nous n’exclurons pas cependant à priori la présence d’une force de répulsion extrêmement grande lors d’un choc intermoléculaire. Nous supposons pour simplifier les molécules toutes identiques et excluons toute modification chimique pouvant intervenir lors des chocs.

Cette définition du gaz parfait introduit en principe la difficulté suivante : les molécules, considérées comme ponctuelles n’ont aucune chance de se rencontrer et les chocs intermoléculaires sont exclus ; comment dès lors la distribution des vitesses correspondant à une température déterminée peut-elle s’établir ?

Nous devrons admettre que ce sont les chocs molécules - parois qui règlent la distribution des vitesses à une certaine distribution d’équilibre où le gaz est en équilibre thermique avec le récipient qui le contient. C’est effectivement ce qui se passe dans les gaz très raréfiés (gaz de Knudsen).

La difficulté de principe devient plus considérable si nous imaginons que le gaz parfait est enfermé dans une enceinte parfaitement adiabatique. Les parois de l’enceinte ne peuvent, en principe, échanger de l’énergie avec les molécules du gaz. Une molécule de très grande vitesse introduite dans l’enceinte garderait dès lors cette vitesse indéfiniment et l’équilibre thermique d’ensemble ne pourrait être obtenu.

Il suffira, pour lever la difficulté, d’admettre qu’une très petite quantité de substance diatherme (de capacité calorifique négligeable) est introduite dans l’enceinte avec le gaz parfait. Les échanges d’énergie entre les diverses molécules peuvent alors avoir lieu par l’intermédiaire d’échanges d’énergie avec cette substance.

Une difficulté analogue est rencontrée dans le cas d’une assemblée de photons enfermée dans une enceinte parfaitement réfléchissante (voir plus loin le rayonnement thermique).

En mécanique statistique, on tourne ce genre de difficulté en supposant que les interactions entre les divers éléments de l’assemblée considérée (ici des molécules) sont infiniment faibles, mais pas tout à fait nulles. La mise à l’équilibre thermique (on dit aussi thermalisation) reste alors possible bien que l’on puisse traiter les divers éléments de l’assemblée comme indépendants.

3. Gaz parfait. Interprétation statistique de la pression

Rappelons que la pression est numériquement égale à la force normale exercée par le gaz sur l’unité de surface de l’enceinte qui contient le gaz. Elle est due à la multitude des chocs exercés sur la paroi par les molécules par suite de leur continuelle agitation.

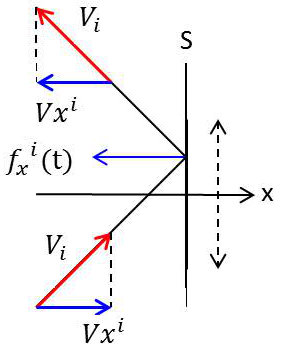
Considérons donc cette unité de surface. De façon régulière, toute molécule venant heurter cette surface \(S\) exerce sur elle une force relativement importante, pendant la durée très brève du choc.

Il en résulte que cette surface est soumise à un effort moyen égal à la valeur moyenne de cette force pendant un intervalle de temps quelconque, par exemple 1 seconde. La force moyenne, c’est-à-dire la pression est dirigée suivant la normale \(Ox\) à la paroi. Seule intervient donc pour calculer la moyenne, la composante suivant \(Ox\) de la force instantanée, soit \(f_x(t)\) : \[P=\frac{1}{t}\int_0^1 f_x(t)~dt\qquad\text{ou bien}\quad P=\int_0^1 f_x(t)~dt\]

Nous ne connaissons pas la loi de force \(f_x(t)\), mais nous savons que celle-ci résulte de la superposition des actions individuelles des diverses molécules venant frapper la surface unitaire \(S\) pendant 1 seconde.

Nous pouvons séparer dans l’intégrale les divers termes correspondant aux divers chocs moléculaires. Au \(i^{\text{ème}}\) choc correspond une force \(f_x^i(t)\) qui n’apparaît que pendant la durée très brève de ce choc et qu’il suffit d’intégrer pendant la durée \(\varepsilon\) du choc.

On a donc : \[P = \sum_i\int_{ti}^{ti+\varepsilon}f_x^i(t)~dt\]

L’instant \(t_i\) est celui du début du \(i^{eme}\) choc.

Soit alors \(V_x^i\) la vitesse suivant \(Ox\) de la molécule responsable du \(i^{eme}\) choc ; immédiatement avant le choc, cette composante de vitesse est positive.

Soit \({V'}_x^i\) sa vitesse suivant \(Ox\) après le choc contre la paroi. Cette composante est négative, mais pas forcément opposée à \(V_x^i\), car la paroi n’est nullement plane à l’échelle atomique et il n’y a aucune raison de supposer que le rebondissement de la molécule suit les lois de la réflexion lumineuse.

Pendant la durée du choc, la vitesse de la molécule est \(V_x^i(t)\), la composante suivant \(Ox\) de force quelle exerce sur la paroi \(S\) est \(f_x^i(t)\)  : elle subit donc de la paroi une force opposée \([f_x^i(t)]\) et nous pouvons écrire constamment, puisque la paroi est seule à exercer une force sur la molécule (pas de forces intermoléculaires) : \[m~\frac{d}{dt}~\{V_x^i(t)\}=-f_x^i(t)\]

Intégrons pendant la durée du choc : \[m~({V'_x}^i-V_x^i)=\int_{ti}^{ti+\varepsilon} -f_x^i(t)~dt\]

Et comme les molécules sont supposées toutes identiques, donc de même masse \(m\) : \[p=m~\sum_i(V_x^i-{V'}_x^i)=m~\Big(\sum_iV_x^i-\sum_i{V'}_x^i\Big)\]

Mais le rebondissement sur la paroi ne modifie pas la répartition d’équilibre des grandeurs des vitesses (hypothèse initiale). On a donc : \[\Big|\sum_iV_x^i\Big|=\Big|\sum_i{V'}_x^i\Big|\]

Tous les \(V_v^i\) sont positifs et tous les \({V'}_x^i\) sont négatifs, on peut écrire : \[\sum_i{V'}_x^i=-\sum_iV_x^i\]

Par suite : \[p=2~m~\sum_iV_x^i\]

La somme étant étendue à l’ensemble des molécules venant frapper en 1 seconde l’unité de surface \(S\). Cherchons à calculer cette somme et isolons pour cela les molécules ayant une vitesse \(V_x\) positive comprise entre \(u\) et \(u + du\).

Parmi ces molécules, dont le nombre par unité de volume est \(dn\) celles qui viennent frapper la surface \(S\) entre les instants \(t\) et \(t + dt\) sont celles qui se trouvaient à l’instant \(t\) à une distance inférieure à \(u~dt\) de la paroi.

Leur ensemble fournit la contribution \(2m~dn~u^2~dt\) pendant l’intervalle \(dt\), soit, en intégrant sur un intervalle de temps égal à une seconde, une contribution des molécules de vitesse suivant \(Ox\) égale à la valeur déterminée \(u\), à \(du\) près : \(2m~dn~u^2\).

Pour avoir la somme complète résultant de l’ensemble des molécules de vitesse \(V_x\) quelconque mais positive, il suffit d’intégrer sur l’ensemble des valeurs positives de \(u\) et d’introduire la vitesse quadratique moyenne suivant \(Ox\) des molécules du gaz :

\[p=2~m~\sum_iV_x^i=2~m\int_0^{\infty} u^2~dn=2~m~\frac{n}{2}~\overline{u^2}\]

En remarquant que parmi ces molécules en nombre \(n\), il n’y en a que \(n/2\) qui ont une composante de vitesse \(V_x\) positive, on peut écrire :

\[\begin{aligned} &\int_0^{\infty} u^2~dn=\frac{1}{2}\int_{-\infty}^{+\infty} u^2~dn=\frac{n}{2}~\overline{u^2}\\ u^2&=v^2=w^2=\frac{u^2+v^2+w^2}{3}=\frac{\overline{c^2}}{3}=\frac{C^2}{3}\end{aligned}\]

Et il vient donc : \[p=\frac{n~m~C^2}{3}\]

Considérons à présent le cas du volume moléculaire \(V\). On écrira (pour se rapprocher de la loi des gaz parfaits) : \[p~V=N~\frac{m~C^2}{3}=\Big(\frac{2}{3}~N\Big)\times\Big(\frac{mC^2}{2}\Big)\]

où \(N=6,02\times 10^{23}\) est le nombre d’Avogadro.

En notant que \(m~C^2/2\) représente l’énergie cinétique moyenne de translation d’une molécule et comparant à la formule des gaz parfaits pour une mole : \(p~V=R~T\).

Nous en arrivons à la relation :

\[\begin{aligned} \frac{m~C^2}{2}&=\frac{3}{2}~k~T\\ k=\frac{R}{N}&=1,38\times 10^{-23}~J/s\qquad\text{Constante de Boltzmann}\end{aligned}\]

Remarquons immédiatement que \(k\) étant une constante universelle, l’énergie cinétique moyenne des molécules d’un gaz parfait à la température \(T\) est la même pour tous les gaz et ne dépend que de la température.

Remarque

Considérons à présent un mélange de gaz parfaits de volume \(V\), contenant \(n_i\) moles du gaz \(G_i\) dont les molécules ont la masse \(m_i\), etc.

Nous avons admis que le gaz \(G_i\) occupe tout le volume \(V\) à la pression partielle \(p_i\) telle que \(p_i~V=n_i~R~T\). Cette pression partielle est évidemment due aux chocs sur les parois de l’enceinte des molécules du gaz \(G_i\) et nous pouvons écrire : \[p_i~V=\frac{2}{3}~n_i~N~m_i~\frac{C_i^2}{2}=n_i~R~T\]

On a donc pour le mélange : \[\frac{m_1~C_1^2}{2}=\frac{m_2~C_2^2}{2}=\dots=\frac{m_i~C_i^2}{2}=\dots=\frac{3}{2}~k~T\]

L’énergie cinétique moyenne de translation est la même pour les divers types de molécules constituant le mélange à l’équilibre. Nous exprimons ce résultat en disant qu’il y a équipartition de l’énergie cinétique de translation entre les divers types de molécules.

Nous pourrons exprimer mathématiquement cette équipartition en remarquant que la vitesse de translation d’une particule peut s’exprimer au moyen de trois paramètres, à savoir les vitesses de translation suivant les trois axes de coordonnées \((V_x,~V_y,~V_z)\).

Les mouvements de translation sont donc des mouvements à trois degrés de liberté. À chacun de ces degrés de liberté est affectée, à l’équilibre, à la température \(T\), une énergie cinétique moyenne \(k~T/2\), la même suivant les trois directions et la même pour tous les types de molécules du mélange de gaz parfaits.

4. Vitesse quadratique moyenne

La vitesse quadratique moyenne est déduite de l’équation : \[\frac{m~C^2}{2}=\frac{3}{2}~k~T\quad\Rightarrow\quad C=\sqrt{\frac{3~k~T}{m}}= \sqrt{\frac{3~R~T}{M}}\]

La vitesse quadratique moyenne à la température T des molécules du gaz G est donc inversement proportionnelle à la raciné carrée de la masse moléculaire M. À température donnée, cette vitesse quadratique moyenne est donc d’autant plus grande que le gaz est plus léger.

À titre d’exemple et à 0 °C, on a : \[\begin{aligned} &\text{Hydrogène~:}& & M=2,016\quad& & C=1838~m/s\\ &\text{Oxygène~:}& & M=32& & C=461~m/s \end{aligned}\]

Remarquons aussi que la constante \(h\) que nous avions laissé subsister dans la fonction de répartition des vitesses se trouve maintenant déterminée en fonction de la température absolue du gaz en équilibre.

On a en effet : \[C^2=\frac{3~k~T}{m}=\frac{3}{2~h~m}\quad\Rightarrow\quad h=\frac{1}{2~k~T}\]

D’où l’expression définitive de la probabilité : \[P(u,~v,~w)~du~dv~dw=\Big(\frac{m}{2\pi~k~T}\Big)^{3/2}~\exp\Big\{-\frac{1}{k~T}~\frac{m}{2}~(u^2+v^2+w^2)\Big\}~du~dv~dw\]

La probabilité pour que le point représentatif de la vitesse d’une molécule se situe dans une petite cellule \(d\tau\) de l’espace des vitesses pour laquelle l’énergie cinétique de translation est \(E\) est donc proportionnelle à la quantité : \[\exp\Big(-\frac{E}{k~T}\Big)~d\tau\]

Cette formule est susceptible d’importantes généralisations.

Remarquons que la probabilité y est rapportée à une petite cellule de l’espace des vitesses, ou encore de l’espace des moments (quantités de mouvement) et non à un intervalle de l’énergie cinétique.

5. Énergie de translation et énergie interne

Considérons une mole de gaz parfait (contenant N molécules).

La somme des énergies de ces diverses molécules en équilibre à la température T est : \[E_c=\sum\frac{m~c^2}{2}=N~\frac{m~C^2}{2}=\frac{M~C^2}{2}=N~\frac{3}{2}~k~T=\frac{3}{2}~R~T\]

Faisons varier la température de \(dT\). Dans le nouvel équilibre, l’énergie des molécules a varié de : \[dE_c=\frac{3}{2}~R~dT\]

Nous allons comparer cette expression à la variation d’énergie interne de la mole de gaz parfait considérée et étudier plusieurs cas, ceux d’un gaz monoatomique et d’un gaz diatomique.

5.1. Gaz monoatomique

On a alors (aux températures usuelles) : \[\frac{C_p}{C_v}=\frac{5}{3}\qquad;\qquad C_p-C_v=R\]

On en déduit : \[C_p=\frac{5~R}{2}\qquad;\qquad C_v=\frac{3~R}{2}\]

On a alors: \[dU~=~dE_c~=~\frac{3}{2}~R~dT\]

L’énergie cinétique de translation est donc, pour un gaz monoatomique, la seule forme d’énergie susceptible de varier lors d’une variation de température.

5.2. Gaz diatomique

On a alors (aux températures usuelles) : \[\frac{C_p}{C_v}=\frac{7}{2}\qquad;\qquad C_p-C_v=R\]

On en déduit : \[C_p=\frac{7~R}{2}\qquad;\qquad C_v=\frac{5~R}{2}\]

On a alors : \[dU~=~\frac{5}{2}~R~T~>~dE_c\]

L’énergie de translation n’est donc plus la seule forme d’énergie susceptible de varier lors d’une variation de température.

Le même résultat serait obtenu pour des gaz polyatomiques.

Pour interpréter ces résultats nous remarquerons tout d’abord qu’il n’y a à priori aucune raison pour limiter aux seules translations les mouvements possibles des molécules. Nous devons également envisager des mouvements de rotation de la molécule autour d’un axe passant par son centre et aussi des vibrations internes pour les molécules polyatomiques.

Introduisons alors un principe beaucoup plus général d’équipartition de l’énergie suivant lequel :

À chaque degré de liberté et à chaque forme d’énergie (cinétique ou potentielle) est affectée en moyenne par molécule, lorsque l’équilibre à la température \(T\) est établi, la même quantité d’énergie \(k~T/2\).

Nous devrions alors obtenir :

• Pour les molécules monoatomiques :

  Pas de vibrations mais trois degrés de liberté pour les translations et trois autres pour les rotations (trois composantes du vecteur vitesse angulaire).

  Soit une énergie moyenne \(3~k~T\) par molécule et une capacité calorifique moléculaire \(CV~=~3~R\).

• Pour les molécules diatomiques :

  Six degrés de liberté correspondant aux translations et rotations et un degré de liberté correspondant aux vibrations le long de l’axe des deux noyaux atomiques.

  À une telle vibration correspondent deux formes d’énergie (cinétique et potentielle) et on doit lui attribuer l’énergie \(k~T\).

Ce qui fait au total \(4~k~T\) pour l’énergie moyenne des molécules et une capacité calorifique moléculaire \(CV~=~4~R\).

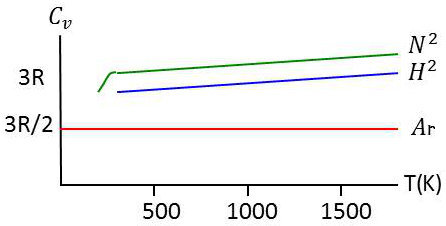Les courbes expérimentales de variation avec la température les capacités calorifiques moléculaires \(C_V\) d’un gaz monoatomique, l’argon, et de deux gaz diatomiques, l’hydrogène et l’azote, montrent que :

• pour l’argon \(C_V = 3~R/2\) à toutes les températures réalisables ;

• pour les deux autres gaz, \(C_V = 5~R/2\) aux températures usuelles, valeur dépassée aux très hautes températures ;

• pour l’hydrogène à très basse température \((T < 50~K)\), la capacité \(C_V\) rejoint la valeur \(3~R/2\) qui correspond aux gaz monoatomiques tels que l’argon.

Il est bien évident en effet que ce n’est que par de tels échanges d’énergie lors de chocs moléculaires que sont susceptibles de s’égaler à la valeur moyenne \(k~T/2\) les diverses formes d’énergie contenues dans la molécule.

L’énergie interne des noyaux atomiques par exemple est énorme, comme le montrent les réactions nucléaires, mais elles ne passent pas d’une molécule à l’autre dans un simple choc aux températures usuelles. Le principe d’équipartition de l’énergie ne saurait donc s’appliquer à l’énergie interne des noyaux atomiques, énergie qui reste emprisonnée dans chacun des noyaux.

Il semblerait bien par contre que l’énergie cinétique de rotation puisse être apportée à une molécule par un simple choc tangentiel d’une autre molécule et qu’elle soit ainsi susceptible de s’échanger, et par suite de s’égaler, avec l’énergie cinétique de translation.

Ceci serait vrai si l’énergie cinétique de rotation d’une molécule pouvait prendre n’importe quelle valeur ; des chocs tangentiels pourrait progressivement l’amener en rotation, de même qu’une molécule immobile est amenée progressivement à la vitesse d’agitation thermique par le bombardement répété des autres molécules.

Nous allons voir qu’il est impossible d’accroître progressivement la vitesse de rotation d’une molécule.

6. Chaleurs spécifiques de gaz parfait. Interprétation cinétique

6.1. Limitations quantiques

On rappelle que le moment cinétique d’un corps tournant autour d’un axe passant par son centre de gravité est \(M=I~\omega\). La mécanique classique considère comme possibles toutes les valeurs de \(M\) et par suite toutes celles de \(\omega\).

À l’échelle atomique, il faut introduire la mécanique quantique : le moment cinétique est un multiple entier du moment cinétique élémentaire : \[n~\hbar=n~\frac{h}{2\pi}\qquad n~:~\text{entier ;}\quad h~:~\text{constante de Planck}\]

La vitesse angulaire de rotation \(\omega\) ne peut donc varier que par sauts dont la valeur minimum est \((h/2\pi)~I\). Cette valeur est aussi la plus petite vitesse angulaire non nulle possible.

Pour un corps à notre échelle, par exemple une bille de métal, ces sauts de vitesse angulaire sont absolument imperceptibles et la mécanique classique qui admet une variation continue de \(\omega\) est pratiquement valable.

Il n’en est plus de même lorsque \(I\) devient extrêmement faible, comme c’est le cas si le corps considéré est une molécule gazeuse. Le quantum \((h/2\pi)~I\) peut alors prendre des valeurs énormes et la vitesse maximum, non nulle, de rotation est gigantesque.

Passons à l’énergie cinétique de rotation E. \[E=\frac{1}{2}~I~\omega^2=\frac{n^2~h^2}{8~\pi^2~I}\]

Sa valeur minimum non nulle est : \[E_{min}=\frac{h^2}{8~\pi^2~I}\]

Prenons par exemple une molécule d’argon. Elle est formée d’un noyau et d’électrons périphériques. Ces derniers ont une énergie totale bien définie, non susceptible de se modifier dans les chocs tant que la molécule garde sa structure chimique. On pourrait toutefois envisager la mise en rotation du noyau par un choc moléculaire. Ce noyau a pour masse : \[m=\frac{M}{N}=\frac{40\times 10^{-3}}{6,02\times 10^{-23}} \approx 7\times 10^{-26}~kg\]

Son rayon est de l’ordre de   \(r=10^{-15}~cm\).

Son moment d’inertie est de l’ordre de : \[I=\frac{3}{5}~m~r^2\approx 4\times 10^{-54}~\text{unités SI}\]

Il s’ensuit une énergie cinétique de rotation minimum \(E_{min}\approx 10^{-15}~J\), ce qui est une valeur énorme pour une molécule.

La molécule d’argon ne pourra être mise en rotation par le choc tangentiel d’une autre molécule que si l’énergie minimum de l’autre molécule est au moins égale à \(E_{min}\). Or, la probabilité pour qu’une molécule ait une énergie de translation bien supérieure à l’énergie moyenne \(3~k~T/2\) est très faible, cette probabilité décroissant exponentiellement quand \(E\) augmente.

Un choc mettant en rotation la molécule n’aura donc de chance de se produire que si l’énergie moyenne de translation des molécules est au moins de l’ordre de \(E_{min}\) : \[T~>~\frac{E_{min}}{k} \qquad~k~:~\text{constante de Boltzmann}\]

Dans cet exemple, \(T~>~10~K\).

La mise en rotation (ou une modification de l’état de rotation) d’une molécule monoatomique par des chocs moléculaires est donc impossible aux températures usuelles. Les rotations moléculaires n’interviennent donc pas pour le calcul de variation d’énergie interne avec la température et par suite pour le calcul de \(C_V\). Seule l’énergie de translation varie avec \(T\) et nous avons donc bien : \[dU=dE_c=\frac{3}{2}~R~dT\quad\Rightarrow\quad C_V=\frac{3~R}{2}\]

6.2. Cas des gaz diatomiques

Dans le cas des gaz diatomiques, la rotation autour de l’axe commun des noyaux atomique est interdite pour la même raison (inertie trop faible) que dans les gaz monoatomiques. Par contre, les rotations autour d’un axe perpendiculaire à l’axe des noyaux deviennent possibles, car le moment d’inertie de la molécule autour de cet axe est beaucoup plus important.

Par exemple, pour la molécule d’azote dont les deux noyaux de masse : \[m~=~(14\times 10^{-3})\div(6\times 10^{23})~{\rm kg}\]

sont à une distance de l’axe de rotation de l’ordre de \(5\times 10^{-12}~\)m, le moment d’inertie a la valeur approximative : \[I~=~\frac{3}{5}~(2~m)~d^2\approx 10^{-46}~\text{unités SI}\]

Soit une valeur \(2,5\times 10^7\) fois plus forte que dans le cas de la molécule d’argon. Il suffira alors d’une température de l’ordre de 4 K pour que les rotations autour de ce nouvel axe soient possibles.

Ainsi sont introduits deux degrés de liberté de rotation soit une « contribution \(k~T\) » à l’énergie cinétique moyenne et une « contribution \(R\) » à la capacité calorifique moléculaire \(C_V\).

La molécule d’hydrogène est à peu près de mêmes dimensions, mais 14 fois plus légère. Son moment d’inertie est donc 14 fois plus faible et la température devra être de l’ordre de \(4\times 14\approx 60~\)K pour que les rotations puissent s’établir. Il est donc à prévoir qu’aux températures inférieures à 50 K la molécule d’hydrogène se comporte comme une molécule monoatomique. C’est bien ce que montre l’expérience.

Il nous faut enfin envisager pour ces molécules diatomiques la possibilité de vibration des deux atomes le long de leur axe commun. Là encore, la mécanique quantique impose à un tel oscillateur de fréquence \(\nu\) d’avoir une énergie de la forme : \[\Big(n+\frac{1}{2}\Big)~h~\nu\qquad~n~\text{entier}\]

La variation de l’énergie vibratoire lors d’un choc est au moins égale à \(h~\nu\) si elle n’est pas nulle.

Pour que les vibrations moléculaires interviennent dans le calcul de la chaleur spécifique, il faut pour les mêmes raisons que précédemment que \(k~T\) soit au moins de l’ordre de \(h~\nu\).

Dans le cas de l’hydrogène : \(\nu\approx 1,5\times 10^{14}\) (bande d’absorption IR à \(\lambda\approx 2~\mu m)\)

On trouve alors que la condition d’établissement normal des vibrations est : \[T~>~\frac{h\nu}{k}\approx 7000~{\rm K}\]

Nous en concluons pour l’hydrogène que :

• à température supérieure à 7000 K, la capacité moléculaire à volume constant correspondrait à 3 degrés de liberté de translation, 2 degrés de liberté de rotation (contribution \(5~R/2\) et 1 degré de vibration (contribution \(R\)). Elle serait donc \(7~R/2\) ;

• à la température ordinaire, les vibrations ont pratiquement disparu, la capacité calorifique moléculaire doit être \(C_V=5~R/2\) ;

• à très basse température les rotations elles-mêmes disparaissent et \(C_V=3R/2\).

Les résultats expérimentaux se trouvent donc complètement interprétés.