1. La fonction de Helmoltz

On désigne par fonction de Helmotz la fonction d’état : \[F=U-T~S\]

parfaitement définie pour chaque état d’équilibre du système considéré dès que les valeurs de l’énergie interne \(U\) et de l’entropie \(S\) d’un état d’équilibre à une température \(T\) ont été fixées.

1.1. Propriétés de la fonction de Helmoltz

Considérons une transformation réversible élémentaire du système. La variation de la fonction \(F\) est : \[dF=dU-T~dS-S~dT=dW+dQ-T~dS+S~dT\]

Or, \(dQ=T~dS\), car la transformation est réversible.

Il vient donc : \[dF=dW-S~dT\]

Si la transformation réversible est en outre isotherme (\(dT=0\)), on a : \[dF=dW\]

Dans toute transformation isotherme et réversible faisant passer le système d’un état [1] à un état [2], on aura donc : \[W=F_2-F_1=\Delta F\]

Le travail \((-W)\) fourni par le système dans la transformation isotherme et réversible est donc égal à la diminution de la fonction de Helmoltz. C’est pourquoi l’on désigne souvent la fonction \(F\) sous le nom d’énergie libre du système (on dit aussi énergie utilisable). Nous énoncerons ainsi le résultat obtenu :

Dans une transformation isotherme et réversible d’un système quelconque, le travail reçu par le système est égal à son accroissement d’énergie libre.

Remarquons que nous avons dû nous restreindre à des transformations isothermes. Dans une transformation réversible quelconque, le travail reçu n’est pas égal à l’accroissement d’énergie libre ; il serait d’ailleurs absurde de chercher une fonction d’état dont la variation entre l’état initial et l’état final représente le travail reçu par le système au cours de la transformation. Ce travail dépend en effet de tous les états intermédiaires et ne saurait être défini par la seule connaissance de l’état initial et de l’état final.

Ce n’est que si nous spécifions le chemin parcouru par le système que nous connaîtrons le travail reçu pour un chemin isotherme et réversible, il est égal à l’accroissement d’énergie libre. Rappelons que, pour un chemin adiabatique, il est égal à la variation d’énergie interne.

Revenons à l’expression générale relative aux transformations réversibles : \[dF=dW-S~dT\]

Nous savons que \(dW\) peut se mettre dans toute transformation réversible sous la forme : \[dW=X~dx+Y~dy+\dots+Z~dz\]

où \(X,~Y,~\dots,~Z\) représentent des variations de tension et \(x,~y,~\dots,~z\) représentent des variations de quantité. On a donc : \[dF=(X~dx+Y~dy+\dots+Z~dz)- S~dT\]

Soit : \[\Big(\frac{\partial F}{\partial x}\Big)_{y...zT}=X\quad;\quad \dots\quad;\quad \Big(\frac{\partial F}{\partial z}\Big)_{x...yT}=Z\quad;\quad \Big(\frac{\partial F}{\partial x}\Big)_{x...z}=-S\]

Et naturellement toutes les relations exprimant le fait que \(dF\) est une différentielle totale, c’est-à-dire :

\[\begin{aligned} \Big(\frac{\partial X}{\partial y}\Big)_{x...zT}&=\Big(\frac{\partial Y}{\partial x}\Big)_{y...zT}\\ . . . . . . . . . . . . . . &. . . . . . . . . . . . . . . . . \\ \Big(\frac{\partial X}{\partial T}\Big)_{x...zT}&=-\Big(\frac{\partial S}{\partial x}\Big)_{y...zT}\end{aligned}\]

1.2. Application à un système ne recevant de travail que des forces de pression

Dans un système ne recevant de travail que des forces de pression, on aura : \[dF=-p~dv-S~dT\]

Cette relation donne une grande importance à la fonction de Helmoltz en mécanique statistique où elle joue un rôle fondamental. Il est possible en effet de calculer pour certaines substances, par les méthodes de la mécanique statistique, la fonction de Helmoltz \(F\) en fonction de \(T\) et de \(V\).

On en tire immédiatement la fonction d’état par : \[p=-\Big(\frac{\partial F}{\partial v}\Big)_T\]

et l’expression de l’entropie par : \[S=-\Big(\frac{\partial F}{\partial T}\Big)_v\]

Remarquons également que, dans toute transformation réversible, isotherme et à volume constant d’un système ne pouvant recevoir de travail que des forces de pression, \(dF=0\) et par suite \(F\) restent stationnaires.

1.3. Transformations monothermes et irréversibles

Nous supposons qu’au début et à la fin de la transformation, le système est à l’équilibre thermique avec une source de température \(T\), mais par contre n’est pas obligatoirement à l’équilibre thermodynamique, c’est-à-dire qu’il peut être en état de déséquilibre mécanique, chimique, électrique, etc.

La température est bien définie dans les états initial et final. Quant à l’énergie et à l’entropie, il sera toujours possible de les calculer dans l’état final et dans l’état initial, même si l’un de ces états n’est pas un état d’équilibre, à condition que l’on puisse considérer le système comme formé de la juxtaposition de diverses parties séparément à l’équilibre (éventuellement en nombre infini).

Dans la transformation \([1]\rightarrow [2]\), nous aurons alors : \[\begin{matrix} \Delta F\\ 1\rightarrow 2 \end{matrix}~: \qquad F_2-F_1=\Delta U-\Delta(T~S)=\Delta U-T~\Delta S\]

Considérons alors la chaleur \(Q\) reçue par le système (obligatoirement de la source unique), la température \(T\). La variation d’entropie de la source est \([-Q/T]\), celle du système est \([\Delta S]\) et la variation d’entropie de l’Univers est : \[\Delta S+\Big(-\frac{Q}{T}\Big)~>~0\]

On a donc : \[Q<T~\Delta S\]

Et par suite : \[\Delta U-T~\Delta S<\Delta U-Q=W\]

Donc : \[\Delta F~<~W\]

Dans toute transformation monotherme et irréversible joignant deux états d’équilibre thermique avec la source de chaleur d’un système quelconque, l’augmentation d’énergie libre du système est inférieure (en valeur algébrique) au travail qu’il a reçu.

Cela signifie que, pour accroître de façon monotherme et irréversible l’énergie libre de \(W\), il faut dépenser un travail supérieur à \(W\) et que par contre un système subissant une diminution d’énergie libre \(W\) dans une transformation monotherme et irréversible fournit au milieu extérieur un travail inférieur à \(W\).

Il n’est pas indispensable pour le raisonnement que le système reste constamment, au cours de la transformation, à l’équilibre thermique avec la source unique de température \(T\) ; il suffit que la transformation soit monotherme et que l’état initial et l’état final soient des états d’équilibre thermique avec la source de température \(T\).

1.4. Application : réactions chimiques à volume et température extérieure constants

Nous enfermons dans une bombe de volume invariable, à parois diathermes et plongée dans un thermostat de température \(T\), un système de corps chimiques ; nous les supposons initialement séparés par des cloisons à l’intérieur de la bombe ; l’ensemble se met à l’équilibre thermique à la température \(T\). Sa fonction de Helmoltz a une certaine valeur \(F_1\).

Nous brisons les cloisons (sans travail). Les corps réagissent, l’ensemble passe par des états de déséquilibre où même la température peut n’être pas définie. Dans l’état final, les produits de réaction sont de nouveau à l’équilibre thermique à la température \(T\). L’énergie libre est devenue \(F_2\).

Nous pouvons écrire : \[F_2-F_1~<~W\]

Le système ne peut toutefois recevoir de travail que des forces de pression extérieures, le volume de la bombe étant invariable \(W=0\) et par suite \(F_2<F_1\). Nous en concluons que si le système est à l’équilibre thermique avec la source de chaleur unique et maintenu à volume constant, toute évolution spontanée entraînera une diminution de son énergie libre.

Lorsque \(F\) a atteint la valeur minimum compatible avec les liaisons imposées au système, \(F\) ne peut plus diminuer et toute évolution devient impossible ; le système est donc en équilibre. En définitive, la recherche du minimum de la fonction \(F\) nous permettra d’obtenir les conditions d’équilibre d’un système de corps chimiques maintenus à température et volume constant.

2. Fonction de Gibbs

Nous désignons par fonction de Gibbs la fonction d’état : \[G=H-T~S=U+p~v-T~S\]

2.1. Propriétés de la fonction de Gibbs

Dans toute transformation réversible élémentaire : \[dG=dU+p~dv+v~dp-T~dS-S~dT\]

Par ailleurs : \[dU=dQ+dT=T~dS+dW\]

Isolons dans \(dW\) le travail \((_p.dv)\) reçu des forces de pression. Nous écrirons : \[dW=-p~dv+dW'\]

\(dW'\) travail des forces autres que les forces de pression. Il vient alors : \[dG=dW'+v~dp-S~dT\]

D’où nous tirons immédiatement que :

Dans toute transformation isotherme, isobare et réversible d’un système quelconque, la variation de la fonction de Gibbs est égale à la somme des travaux que le système a reçus des forces autres que les forces de pression.

2.2. Transformations irréversibles et monotherme dans un système qui n’est soumis qu’à des forces de pression

Nous supposons que le milieu extérieur de température et de pression constantes. Nous supposons en outre le système à l’équilibre thermique et mécanique avec le milieu extérieur dans l’état initial et dans l’état final (il peut par contre être en déséquilibre chimique par exemple).

La pression, le volume et la température sont donc parfaitement définis dans ces deux états, de même que l’énergie interne et l’entropie. Par contre, nous ne nous intéressons pas à ce qui se passe pendant la transformation, au cours de laquelle la pression et la température peuvent n’être pas uniformes au sein du système.

Soient alors \(G_1,~G_2\) les valeurs de la fonction de Gibbs dans l’état initial et dans l’état final : \[G_1-G_2=\Delta G=\Delta H-\Delta(T~S)=\Delta H-T~\Delta S\]

La chaleur \(Q\) reçue par le système est égale à \(\Delta H\) (transformation à pression extérieure constante).

De plus la source de chaleur est unique et par suite \(Q<T~\Delta S\).

On a donc \(\Delta H<T~\Delta S\) et par suite \(\Delta G<0\) soit \(G_2<G_1\).

Le système étant initialement à l’équilibre de pression et de température avec le milieu extérieur (de caractéristiques invariables), toute transformation spontanée à pression et température extérieures constantes ne peut conduire qu’à une diminution de la fonction de Gibbs.

Laissé à lui-même et maintenu à pression et à température extérieures constantes, le système va donc évoluer jusqu’à ce que sa fonction de Gibbs ait atteint la valeur minimum compatible avec les liaisons imposées au système. Une fois atteint ce minimum, elle ne pourra plus diminuer ; et comme toute évolution réelle exige une diminution de \(G\), toute évolution réelle deviendra impossible : le système sera alors en équilibre.

La fonction de Gibbs joue donc le même rôle pour la recherche de l’équilibre, à pression et à température extérieures constantes, d’un système thermodynamique sensible aux seules forces de pression que l’énergie potentielle pour un système mécanique soumis à un champ de forces invariable ; lorsqu’elle atteint la valeur minimum compatible avec conditions imposées, le système est en équilibre. C’est la raison pour laquelle on désigne souvent la fonction de Gibbs sous le nom de potentiel thermodynamique du système.

En toute rigueur, il faudrait spécifier explicitement qu’il s’agit d’un système qui n’est soumis qu’à des forces de pression, et que ces forces de pression ainsi que la température extérieure sont invariables.

Si l’on maintient constants le volume du système et la température extérieure, nous avons vu que c’est la fonction de Helmoltz qui joue le rôle de potentiel thermodynamique.

Si par contre nous cherchions l’équilibre d’un système isolé, nous remarquerions que toute transformation réelle entraîne une augmentation d’entropie et par suite une diminution de la fonction d’état \((-S)\) qui joue le rôle de potentiel thermodynamique.

C’est pourquoi il est préférable de désigner sous le nom de fonction de Gibbs la fonction \(G\), l’appellation potentiel dynamique devant en toute rigueur être assortie de la précision à pression et température imposée.

3. Fonction de Gibbs généralisée

Nous venons de voir que c’est surtout pour les systèmes sensibles aux seules forces de pression que la fonction \(G=H-T~S\) a des propriétés remarquables. Pour étendre ces propriétés à des systèmes quelconques, électriques ou magnétiques par exemple, nous allons généraliser un peu la fonction de Gibbs.

Soit donc un système soumis à des forces de types divers ; nous savons que dans toute transformation réversible, le travail élémentaire \(dW\) reçu par le système peut être mis sous la forme : \[dW=X~dx+Y~dy+\dots+Z~dz\]

• \(X,~Y,~\dots,~Z\) : variables de tension ;

• \(x,~y,~\dots,~z\) : variables de quantités associées.

Nous désignerons sous le nom de fonction de Gibbs généralisée la fonction : \[G'=U-X~x-Y~y-\dots-Z~z-T~S\]

On voit immédiatement que pour toute transformation réversible : \[dG'=dU-X~dx-Y~dy-\dots-Z~dz-T~dS-x~dX-y~dY-\dots-z~dZ-S~dT\]

Soit en simplifiant : \[dG'=-x~dX-y~dY-z~dZ-S~dT\]

D’où l’on tire : \[\Big(\frac{\partial G'}{\partial X}\Big)_{Y...ZT}=-x~;~\dots~;~ \Big(\frac{\partial G'}{\partial Z}\Big)_{XY...T}=-z~;~ \Big(\frac{\partial G'}{\partial T}\Big)_{XY...Z}=-S\]

Naturellement telles que :

\[\begin{aligned} &\Big(\frac{\partial x}{\partial Y}\Big)_{X...ZT}=\Big(\frac{\partial y}{\partial X}\Big)_{Y...ZT}\\ &\Big(\frac{\partial x}{\partial T}\Big)_{XY...Z}=\Big(\frac{\partial S}{\partial X}\Big)_{Y...ZT}\end{aligned}\]

Relations très utiles lorsque l’état du système a été exprimé à partir de variables de tension (et de température) alors que les relations correspondantes obtenues en écrivant que \(dF\) était une différentielle totale sont commodément utilisables quand l’état du système est exprimé à partir de variables de quantité (et de température).

Remarque

Il reste à considérer le cas où l’état du système serait défini par la température et par certaines variables de quantité \(x,~\dots,~z\) et parles variables de tension associées aux autres variables de quantité, soient \(Y,~\dots,~Z\) (nous évitons de choisir simultanément parmi les variables d’état une variable de quantité et la variable de tension associée, par exemple p et v).

On aura alors intérêt à considérer la fonction de Gibbs généralisée : \[G"=U-T~S-Y~y-\dots-Z~z\]

Dont la différentielle est : \[dG"=dU-T~dS-S~dT-Y~dy-y~dY-\dots\]

C’est-à-dire : \[dG"=X~dx+\dots-\dots-z~dZ-S~dT\]

D’où les relations telles que : \[\Big(\frac{\partial X}{\partial Y}\Big)_{T,x,...Z}=-\Big(\frac{\partial y}{\partial x}\Big)_{T,...Y...Z}\]

Avec naturellement:

\[\begin{aligned} \Big(\frac{\partial G"}{\partial Y}\Big)_{T,x,...Z}&=-y\\ \Big(\frac{\partial G"}{\partial x}\Big)_{T,...Y,...Z}&=X\\ \Big(\frac{\partial G"}{\partial T}\Big)_{x,...Y,...Z}&=-S\end{aligned}\]

Si par exemple l’état du système est défini par la température, la pression et des variables de quantité autres que \(v\), la fonction \(G"\) se réduira à la fonction de Gibbs \(G\).

4. Applications des fonctions de Helmoltz et de Gibbs

Nous allons montrer maintenant comment l’utilisation des fonctions de Gibbs (plus ou moins généralisées) et de Helmoltz permet d’exprimer très simplement, sous forme mathématique, le second principe de la thermodynamique, en nous limitant à des transformations réversibles et isothermes. Il nous suffira d’écrire que les différentielles de ces fonctions sont des différentielles totales, d’où les relations entre dérivées partielles.

Dans le cas où l’état du système est représenté par la température et des variables de quantité, nous utiliserons la fonction de Helmoltz \(F\). Écrire que \(dF\) est une différentielle totale revient, si on se borne à une transformation isotherme et réversible, à écrire que le travail élémentaire \(dW\) est une différentielle totale. On applique donc ainsi directement le second principe. Nous nous placerons dans ce cas particulièrement simple pour le premier exemple.

4.1. Pression osmotique dans la solution d’un gaz parfait

Nous supposons le solvant non volatile et admettons comme point de départ la loi de Henry selon laquelle :

La concentration moléculaire de la solution, à température déterminée (nombre de moles dissoutes / cm³) est proportionnelle à la pression exercée par le gaz sur la solution.

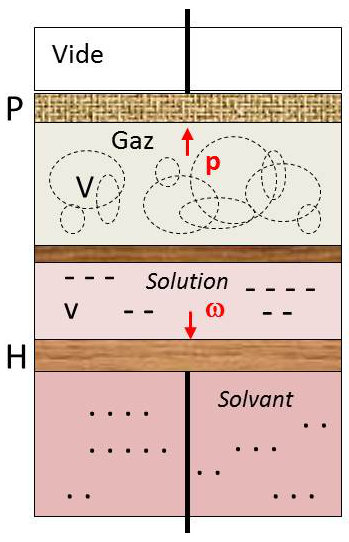Utilisons alors un appareillage expérimental qui va nous permettre de faire varier indépendamment, de façon irréversible, la pression du gaz et le volume de la solution.

Nous considérons le corps de pompe fermé à sa partie supérieure par frottement. Dans la partie inférieure peut coulisser également sans frottement un piston hémiperméable (perméable au solvant seul) ; son déplacement permet de faire varier le volume du solvant pur (bas du corps de pompe) aux dépens du volume de la solution. Le tout est maintenu à une température fixe \(T\) par un thermostat.

L’état du système est alors parfaitement défini (la masse totale de solvant étant fixe) par la simple connaissance du volume \(V\) occupé par la gaz parfait pur (le solvant n’est pas volatile) et du volume \(v\) occupé par la solution.

Le piston \(P\) est soumis à la pression \(p\) du gaz parfait. Le piston \(H\) est soumis à la pression osmotique \(\Pi\) de la solution.

Toute modification réversible et isotherme de l’état du système \([dv,~dV]\) entraîne une variation de la fonction de Helmoltz \(dF=dW\), soit : \[dF=-p~dV-\Pi~dv\]

Nous en tirons immédiatement, \(dF\) étant une différentielle totale : \[\frac{\partial p}{\partial v}=\frac{\partial\Pi}{\partial V}\]

Cherchons à exprimer \(p\) en fonction de \(v\) et \(V\), en appliquant la loi de Henry.

Soit \(n < 1\) le nombre de moles de gaz dissoutes dans le volume \(v\) de la solution. Il y a en tout 1 mole de gaz, et par suite \((1-n\)) moles dans le volume \(V\).

La concentration moléculaire \(n/v\) de la solution est proportionnelle à la quantité \((1- n)/V\) puisque : \[p=R~T~\frac{1-n}{V}\]

Les quantités \(n/v\) et \((1-n)/V\) sont donc proportionnelles et l’on peut écrire : \[\frac{n}{k~v}=\frac{1-n}{V}=1+(k~v+V)\]

\(k\) ne dépendant que de \(T\) qui est fixe ; la seconde égalité est obtenue par addition des numérateurs et dénominateurs.

Nous en tirons : \[1-n=\frac{V}{k~v+V}\]

Par suite : \[p=\frac{R~T}{k~v+V}\]

On a donc : \[\frac{\partial\varpi}{\partial V}=\frac{\partial p}{\partial v}=-\frac{k~R~T}{(k~v+V)^2}\]

Et en intégrant : \[\varpi=\varpi_0+\frac{k~R~T}{k~v+V}\]

Éloignons indéfiniment vers le haut le piston \(P\). Nous extrayons tout le gaz de la solution dont la pression osmotique devient nulle. En même temps, \(V\) tend vers l’infini, ce qui montre que \(\varpi_0=0\).

On a donc : \[\varpi=\frac{k~R~T}{k~v+V}=\frac{n~R~T}{v}\qquad\text{car :}\quad\frac{n}{k~v}=\frac{1}{k~v+V}\]

Nous retrouvons la loi de Vent Hoff \((\varpi~v=n~R~T)\) qui nous apparaît ainsi comme une conséquence de la loi de Henry dans le cas de la solution d’un gaz parfait dans un solvant non volatil.

4.2. Pile réversible dégageant ou absorbant des gaz en fonctionnement

Nous allons étudier à présent le fonctionnement d’une pile réversible dégageant du gaz lorsqu’elle débite du courant, et pour laquelle il est impossible de négliger la variation de volume.

Nous supposons la pile constamment saturée en sels dissous. Sa f.é.m. ne dépend que de la température \(T\) et de la pression \(p\). L’état de la pile est complètement défini par la connaissance de la température \(T\), de la pression \(p\) et de la charge \(q\). En effet, la f.é.m. \(E\) dépend de \(p\) et de \(T\), et le volume \(v\) de \(p\), \(T\) et \(q\).

Quand la pile débite (du pôle + au pôle – à l’extérieur) une charge \(\varepsilon\), sa charge varie de \(dq=-\varepsilon\), elle fournit le travail \(E~\varepsilon\) (on suppose toutes les transformations réversibles) et par suite elle reçoit le travail \(+E~dq\). Enfin, elle reçoit le travail \(-p~dv\) quand son volume varie de \(dv\). Envisageons alors la transformation réversible et isotherme \(dv,~dq\).

La variation de la fonction de Helmoltz est : \[dF=-p~dv+E~dq\]

Comme nous avons choisi \(p,q,T\) pour représenter l’état de la pile, nous aurons donc intérêt à considérer la fonction de Gibbs \(G=F+p~v\).

Si \(T = cte\), sa variation est : \[dG=v~dp+E~dq\]

C’est une différentielle totale et par suite : \[\Big(\frac{\partial v}{\partial q}\Big)_{p,T}=\Big(\frac{\partial E}{\partial p}\Big)_{p,T} =\Big(\frac{\partial E}{\partial p}\Big)_T\]

puisque \(E\) ne dépend que de \(T\) et de \(p\).

Nous voyons ainsi que, si la pile dégage du gaz lorsqu’elle débite dans le sens d’utilisation (\(q\) décroissant), le premier membre est négatif et par suite le second. Il en résulte que sa f.é.m. décroît lorsque la pression augmente à \(T = cte\). C’est l’inverse lorsque la pile absorbe du gaz en fonctionnement.

Nous rencontrons là un premier exemple de la tendance des systèmes physiques à s’opposer aux variations d’état qu’on cherche à leur imposer ; la pile étant en équilibre, sa f.é.m. est équilibrée par un générateur extérieur. Si nous cherchons à augmenter sa pression, elle va s’arranger en variant sa f.é.m. pour que le sens du courant qui la traverse corresponde à une absorption de gaz, contrecarrant ainsi l’augmentation de pression que nous cherchons à réaliser.

4.3. Électrostriction

Nous considérerons un condensateur à diélectrique liquide ; le diélectrique remplit complètement un corps de pompe fermé par un piston qui permet de régler sa pression. Un générateur extérieur permet d’établir une d.d.p. \(V\) entre les armatures. L’état du système est parfaitement défini par la température \(T\), la pression \(p\) et la d.d.p. \(V\).

Nous désignons par \(v\) le volume total, fonction des variables d’état \((p,~V,~T)\) et par \(\varepsilon\) la premittivité du diélectrique que nous supposons indépendante de \(V\), mais fonction de \(T\) et \(p\).

La charge du condensateur est : \[q=\frac{\varepsilon~V~S}{e}\qquad\text{fonction de } p,~V,~T\]

Dans une transformation isotherme et réversible, la fonction de Helmoltz varie de : \[dF=-p~dv+V~dq\]

Compte tenu des variables d’état choisies, nous aurons intérêt à considérer la fonction de Gibbs généralisée : \[G'=F~p~v-V~q\]

dont la différentielle est, pour une transformation isotherme : \[dG'=v~dp-q~dv\]

C’est une différentielle totale et par suite : \[\Big(\frac{\partial v}{\partial V}\Big)_{p,T}=-\Big(\frac{\partial q}{\partial p}\Big)_{V,T}\]

À température constante, une augmentation de pression augmente la densité du diélectrique et par suite sa permittivité, donc la charge du condensateur.

Le second membre est donc négatif ; le premier l’est aussi et nous en déduisons qu’une augmentation de \(V\), à \(p\) et \(T\) constantes, contracte le diélectrique : c’est le phénomène de l’électrostriction.

Calculons la contraction totale \(\delta v\) qui accompagne la charge de \(0\) à \(V\), pour \(p,~T\) constantes. \[dv=\Big(\frac{\partial v}{\partial V}\Big)_{p,T}~dV=-\frac{S}{e}~\Big(\frac{\partial\varepsilon}{\partial p}\Big)_{V,T}~V~dV\]

Soit : \[\delta v=-\frac{S~V^2}{2~e}~\Big(\frac{\partial\varepsilon}{\partial p}\Big)_V\]

Cette contraction ne porte évidemment que sur le volume \(v\) de diélectrique placé entre les armatures et soumis au champ \(E=V/e\).

Nous en déduisons que le volume \(v\) de diélectrique, lorsqu’on le place dans un champ électrique \(E\) subit une contraction relative : \[\frac{\delta v}{v}=-\frac{E^2}{2}~\Big(\frac{\partial\varepsilon}{\partial p}\Big)_{E,T}\]

La contraction est très faible, de l’ordre de \(10^{-7}\) dans un champ de \(5\times 10^6\) V/m pour le sulfure de carbone.

5. Relations de Helmoltz

Considérons toujours le système le plus général, pour lequel une expression du travail élémentaire reçu dans une transformation réversible est : \[dW=X~dx+Y~dy+\dots+Z~dz\]

L’état du système peut être représenté, soit par l’ensemble des variables de quantité \((x,~y,~\dots,~ z)\) et la température \(T\), soit par l’ensemble des variables de tension \((X,~Y,~\dots,~Z)\) et la température.

Nous avons obtenu dans les paragraphes précédents deux relations permettant d’exprimer l’entropie \(S\) du système, soit à partir de la fonction de Helmoltz, soit à partir de la fonction de Gibbs généralisée, en l’occurrence : \[S=-\Big(\frac{\partial F}{\partial T}\Big)_{x,y,...,z}\quad;\quad S=-\Big(\frac{\partial G'}{\partial T}\Big)_{X,Y,...,Z}\]

Portant ces expressions de \(S\) dans la relation qui définit \(F\), nous obtenons :

\[\begin{aligned} &U=F-T~\Big(\frac{\partial F}{\partial T}\Big)_{x,y,...,z}\\ &U=F-T~\Big(\frac{\partial G'}{\partial T}\Big)_{X,Y,...,Z}\end{aligned}\]

que nous pouvons écrire de façon plus symétrique :

\[\begin{aligned} U&=F-T~\Big(\frac{\partial F}{\partial T}\Big)_{x,y,...,z}\\ U-X~x-Y~y-\dots-Z~z&=G'-T~\Big(\frac{\partial G'}{\partial T}\Big)_{X,Y,...,Z}\end{aligned}\]

Ces relations portent le nom de relations de Helmoltz. Elles sont toutes deux valables pour tout état d’équilibre du système et elles sont d’ailleurs strictement équivalentes.

La première s’appliquera commodément dans le cas d’un système dont l’état est représenté par ses variables de quantité et sa température, la seconde lorsque l’état du système est représenté par ses variables de tension et sa température.

Ce choix n’est évidemment pas indispensable. On pourrait évidemment utiliser la première qui est parfaitement valable, dans le cas où les variables choisies sont des variables de tension \(X,~\dots,Z\), mais la dérivée partielle \((\partial F/\partial T)_{x,y,...,z}\) ne s’obtient pas naturellement par simple dérivation et nécessite un changement de variables ; il est donc bien plus simple d’utiliser la seconde dans ce cas.

6. Application pratique des relations de Helmoltz

Telles que nous les avons écrites, les relations de Helmoltz lient les fonctions \(U,~F\) ou \(U,~G'\) dont la mesure absolue n’est pas expérimentalement accessible. Pour obtenir des relations entre grandeurs expérimentalement mesurables, il nous faut les transformer de façon à faire apparaître les variations des fonctions \(U,~F,~G'\) dans une transformation donnée, variations qui, elles, sont parfaitement définies au point de vue expérimental.

Nous remarquons alors que la variation de \(F\) dans une transformation isotherme et réversible est égale au travail reçu par le système, travail aisément calculable à partir des variables thermodynamiques du système.

La première relation de Helmoltz par exemple va nous permettre d’établir très simplement une relation entre le travail reçu par le système dans une transformation isotherme et réversible (variation d’énergie libre) et la chaleur reçue dans la même transformation (variation d’énergie liée).

Choisissons les variables \((T,~x,~y,~\dots,~z)\) pour représenter l’état d’équilibre du système et considérons une transformation isotherme et réversible faisant passer le système de l’état \((T,~x_1,~y_1,~\dots,~z_1)\) à l’état \((T,~x_2,~y_2,~\dots,~z_2)\). Le travail reçu par le système dans cette transformation est : \[W_T=F(T,~x_2,~...,~z_2)-F(T,~x_1,~...,~z_1)= \begin{matrix} &(\Delta F)_T\\ &1\rightarrow 2 \end{matrix}\]

et sa variation d’énergie interne : \[W_T+Q_T=U(T,~x_2,~...,~z_2)-U(T,~x_1,~...,~z_1)= \begin{matrix} &(\Delta U)_T\\ &1\rightarrow 2 \end{matrix}\]

Et nous pouvons écrire, pour l’état initial et pour l’état final :

\[\begin{aligned} &U(T,~x_1,~...,~z_1)=F(T,~x_1,~...,~z_1)-T~\Big(\frac{\partial F}{\partial T}\Big)_{x1,~...,~z1}\\ &U(T,~x_2,~...,~z_2)=F(T,~x_2,~...,~z_2)-T~\Big(\frac{\partial F}{\partial T}\Big)_{x2,~...,~z2}\end{aligned}\]

Faisant la différence, il vient : \[\begin{matrix} &(\Delta U)_T\\ &1\rightarrow 2 \end{matrix} = \begin{matrix} &(\Delta F)_T\\ &1\rightarrow 2 \end{matrix} - T~\Big\{\frac{\partial(\Delta F)}{\partial T}\Big\}_{x1,...,z1,~x2,...,z2}\]

Les variables de quantité \(x_1,~...,~z_1,~x_2,~...,~z_2\) mises en indice indiquent que l’on doit considérer la variation de \(\Delta F\) (c’est-à-dire du travail \(W\) reçu au cours de la transformation) lorsque l’on fait varier la température de transformation sans faire varier les variables de quantité qui caractérisent l’état initial et l’état final.

Illustrons ceci dans le cas simple d’un système sensible aux seules forces de pression, en l’occurrence un système chimique dont nous supposons chaque instant d’équilibre déterminé par la connaissance de la température et du volume total.

Dans la transformation faisant passer le système de l’état \([T,v_1]\) à l’état \([T,v_2]\) (transformation isotherme et réversible) les variations d’énergie interne et d’énergie libre sont liées par : \[\Delta U=\Delta T-T~\Big\{\frac{\partial(\Delta F)}{\partial T}\Big\}_{v1=cte,~v2=cte}\]

Remarquons par ailleurs que, la transformation étant isotherme et réversible : \[\Delta F=W\quad\Rightarrow\quad\Delta U-\Delta F=Q\]

Nous pourrons écrire dans le cas général : \[\begin{matrix} &Q_T\\ &1\rightarrow 2 \end{matrix} =-T~\Big\{\frac{\partial(\Delta F)}{\partial T}\Big\}_{x1,...,z1,~x2,...,z2}\]

Et dans le cas particulier de notre système chimique : \[\begin{matrix} &Q_T\\ &1\rightarrow 2 \end{matrix} =-T~\Big\{\frac{\partial(\Delta F)}{\partial T}\Big\}_{v1=cte,~v2=cte}\]

relation qui, jointe à : \[\begin{matrix} &W_T\\ &1\rightarrow 2 \end{matrix} = \begin{matrix} &(\Delta F)_T\\ &1\rightarrow 2 \end{matrix}\]

lie la chaleur reçue par le système dans la transformation isotherme et réversible au travail qu’il reçoit en même temps, ou plutôt à la variation de ce travail lorsque la température de transformation est modifiée, les variables de quantité qui en fixent les limites restant constantes.

Application : formule de Clapeyron donnant la chaleur latente de vaporisation

Nous considérons la transformation isotherme et réversible faisant passer, à la température \(T\), une masse de 1 gramme de fluide de l’état liquide de saturation (volume \(u\)) à l’état vapeur saturante (volume \(u'\)). La pression de vapeur est \(p\) et ne dépend que de \(T\) :

– Travail reçu : \(W=-p~(u'-u)=\Delta F\)

– Chaleur reçue : \(L\)

On a donc : \[L=-T~\Big\{\frac{\partial[-p(u'-u)]}{\partial T}\Big\}_{u',~u=cte}\]

Soit : \[L=T(u'-u)~\frac{dp}{dT}\]

C’est la formule de Clapeyron.

7. Condensateur à diélectrique

Nous reprenons le condensateur à diélectrique liquide pour lequel nous avons étudié plus haut le phénomène de l’électrostriction. Nous représentons son état par la température \(T\), la tension appliquée aux armatures \(V\), et la pression imposée \(p\).

Le volume \(v\) est fonction de \(T,~p\) et un peu de \(V\) par suite de l’électrostriction. La charge \(q\) est fonction de \(V\) et de la permittivité \(\varepsilon\), par suite de \(V,~p,~T\) (nous supposons \(\varepsilon\) fonction de \(T\) et \(p\), mais pas de \(V\)).

L’expression du travail élémentaire est : \[dW=V~dq-p~dv\]

soit la fonction de Gibbs généralisée : \[G'=U-T~S+p~v-V~q\]

dont la différentielle est : \[dG'=v~dp-q~dV-S~dT\]

La charge à \(p\) et \(T\) constantes de la tension \(0\) à \(V\) entraîne une variation de la fonction de Gibbs : \[\Delta G'=-\int q~dv=-\frac{S~V^2}{2~e~\varepsilon(p,~T)}\]

et une variation d’énergie interne :

\[\begin{aligned} &\Delta U=\Delta F-T~\Big\{\frac{\partial(\Delta G')}{\partial T}\Big\}_{p,v}\\ &\Delta U=\Delta F+\frac{T~S~V^2}{2~e~\Big(\cfrac{\partial\varepsilon}{\partial T}\Big)_p}\end{aligned}\]

\(F\) est égal à \(W\), travail reçu par le condensateur. Celui-ci reçoit donc, pendant la charge du thermostat qui maintient sa température \(T\), la chaleur : \[Q=\Delta U-\Delta F=\frac{T~S~V^2}{2~e~\Big(\cfrac{\partial\varepsilon}{\partial T}\Big)_p}\]

Si la pression n’est pas énorme, le travail reçu pendant la charge se réduit pratiquement au travail électrique \(\varepsilon~S~V^2/2~e\), car la variation de volume due à l’électrostriction est extrêmement faible.

On a donc pratiquement : \[\Delta U\approx\frac{S~V^2}{2e~\Big(\varepsilon+T~\cfrac{\partial\varepsilon}{\partial T}\Big)}=W_{el}~\Big(1+T~\frac{1}{\varepsilon}~\frac{\partial\varepsilon}{\partial T}\Big)\]

Le second terme du crochet est négatif et nullement négligeable devant l’unité. Il vaut (–1/4) environ pour le sulfure de carbone à la température ordinaire. La variation d’énergie interne du condensateur durant la charge n’est donc que les trois quarts du travail électrique qu’il a reçu.

Il serait donc faux de considérer qu’on a emmagasiné dans le condensateur l’énergie dépensée pendant que la charge libre a été accrue de \(W_{el}\) et que pendant la décharge on récupérera la totalité de l’énergie électrique \(W_{el}\) sous forme de travail, énergie qui se trouve alors supérieur à la diminution d’énergie interne, le complément étant fourni par le thermostat sous forme de chaleur intégralement convertie en travail.

8. Pile irréversible. Équation de Gibbs-Helmoltz

Une autre application importante des relations de Helmoltz va maintenant être rencontrée dans la théorie thermodynamique de la pile réversible.

Nous représentons son état par la température \(T\), la pression \(p\) et la charge \(q\). L’électrolyte est supposé formé d’une solution saturée, de telle sorte que sa f.é.m. \(E\) dépend de la température et de la pression, mais pas de la charge \(q\). Le volume \(v\) dépend de \(T,~p,~q\) (possibilité de dégagement de gaz lors de la charge ou de la décharge).

Le travail élémentaire dans une transformation réversible est : \[dW=E~dq-p~dv\]

Nous aurons donc intérêt à considérer la fonction de Gibbs : \[G=U-T~S+p~v\]

dont la différentielle est : \[dG=v~dp+E~dq-S~dT\]

Dans le débit par la pile d’une charge égale à \(q_0\) à pression et température constantes, la fonction de Gibbs varie de (\(-E~q_0\)).

Nous supposons que la réaction chimique qui s’effectue dans la pile s’écrit : \[\sum_i\nu_i~A_i\quad\rightarrow\quad\sum_j \nu'_j~A'_j\]

la réaction ayant lieu vers la droite lorsque la pile débite du courant du pôle \((+)\) au pôle \((-)\) à l’extérieur.

Soit \(n\) la valence de l’électrolyte ; la réaction que nous avons écrite transforme les \(\nu'_i\) moles de \(A_i\) en \(\nu'_j\) moles de \(A'_j\), etc. lors du débit d’une charge \(q=n_0~F\) (\(F\) : constante de Faraday).

Supposons donc que la pile débite \(n~F\) coulombs à \(T\) et \(p\) constantes.

La variation de la fonction de Gibbs est \(\Delta G=-n~F~E\).

Et la relation de Helmoltz nous apprend qu’il s’ensuit pour la pile une variation d’enthalpie : \[H=\Delta G-T~\Big\{\frac{\partial(\Delta G)}{\partial T}\Big\}_{p,q_0}=-n~F~\Big\{E-T~\Big(\frac{\partial E}{\partial T}\Big)_p\Big\}\]

La même variation d’enthalpie aurait lieu si la réaction chimique s’effectuait à la même température et à la même pression de façon irréversible, sans intervention de travail électrique. Cette réaction dégagerait alors une quantité de chaleur égale à \(Q_p\), chaleur de réaction à pression constante, avec : \[Q_p=-\Delta H\qquad\text{d’après le premier principe}\]

Nous avons donc : \[E-T~\Big(\frac{\partial E}{\partial T}\Big)_p=\frac{Q_p}{n~F}\qquad\text{équation de Gibbs-Helmoltz}\]

relation très importante qui permet grâce à des mesures purement électriques de prévoir la valeur de \(Q_p\) à diverses températures et d’en déduire, comme nous le verrons, la marche de la réaction chimique.

Si la pile ne dégage pas de gaz lors de son fonctionnement, les variations de volume sont négligeables ; la pression choisie n’étant pas énorme, nous pourrons poser sans erreur appréciable : \(\Delta H=\Delta U\). Là encore la variation d’énergie interne de la pile est différente du travail \((+nFE)\) qu’elle fournit au milieu extérieur, la différence provenant de la chaleur fournie par le thermostat qui maintient constante sa température.

Remarquons en outre que pour une pile ne dégageant pas de gaz, \(E\) ne dépend pas sensiblement de \(p\). Nous écrirons alors simplement : \[E-T~\frac{dE}{dT}=\frac{Q_p}{n~F}\]

Le signe de la chaleur de réaction ne suffit donc pas à déterminer le signe de \(E\), c’est-à-dire la polarité de la pile. Il peut arriver dans des cas exceptionnels que la réaction qui se produit dans la pile lorsqu’elle débite du courant (fournissant ainsi du travail) soit une réaction endothermique. La pile voit alors son énergie interne augmenter bien qu’elle fournisse du travail au milieu extérieur. Il est clair que toute l’énergie est alors fournie par le thermostat sous forme de chaleur.

Un exemple classique est celui de la pile \([Hg-Hg_2Cl_2-KCl-KOH-Hg_2O-Hg]\) pour laquelle \(E=0,35~V\) bien que la réaction : \[Hg_2Cl_2+2~KOH~~\rightarrow~~Hg_2O+H_2O+2~KCl\]

soit endothermique : \[\frac{Q_p}{n~F}=-0,14~V\]

du fait que : \[\frac{dE}{dT}\approx 1,6~mV/K\]

et que par suite, à la température ordinaire: \[T~\frac{dE}{dT}=0,49~V\]

9. Intégration de l’équation de Gibbs-Helmoltz

Convenons d’utiliser la pile à une pression fixe, par exemple la pression atmosphérique. Même si elle dégage du gaz, nous pourrons alors considérer \(E\) comme fonction de \(T\) seulement et écrire : \[E-T~\frac{dE}{dT}=\frac{Q_p}{n~F}\]

Soit encore : \[\frac{d}{dT}\Big(\frac{E}{T}\Big)=\frac{1}{T}~\frac{dE}{dT}-\frac{E}{T^2}=-\frac{Q_p}{n~F~T^2}\]

\(Q_p\) ne dépend que de la température et nous avons établi que : \[\frac{dQ_p}{dT}=\sum_i\nu_i~C_{pi}-\sum_j\nu'_j~C'_{pj}\]

les \([C_{pi},~C'_{pj}]\) étant les capacités calorifiques moléculaires à pression constante des corps \(A_i,~A'_j\).

Dans un intervalle de température qui n’est pas trop étendu, nous pourrons représenter par des formules linéaires les variations des \(C_p\) avec la température, arrivant ainsi à : \[\Delta C_p=\sum_j C'_{pj}~\nu'_j-\sum_j C_{pi}~\nu_i=\Delta C_p^0+2a~T\]

en désignant part \(2a\) une certaine constante.

On a alors : \[-Q_p=\Delta H^0+T~\Delta C_p^0+a~T^2\]

Soit : \[n~F\frac{d}{dT}\Big(\frac{E}{T}\Big)=\frac{\Delta H^0}{T^2}+\frac{\Delta C_p^0}{T}+a\]

d’où : \[n~F~E=-\Delta H^0+\Delta C_p^0~T~\ln(T)+a~T^2+b~T\]

\(b\) est une constante d’intégration. \(\Delta H^0,~\Delta C_p^0\) peuvent être déterminées par des mesures calorimétriques. Il suffit de mesurer \(E\) à une température quelconque pour obtenir la constante \(b\).

L’équation de Gibbs-Helmoltz permet donc soit de déterminer des chaleurs de réaction par voie purement électrique (voltmètre et thermomètre), soit de prévoir la f.é.m. d’une pile à température quelconque à partir de données purement calorimétriques.

10. Capacités calorifiques d’un système chimique

Les capacités calorifiques à \(p\) ou \(v\) constants d’un système chimique (sensible aux seules forces de pression) s’expriment très simplement à partir des fonctions de Helmoltz et de Gibbs.

Des relations :

\[\begin{aligned} &dF=-p~dv-S~dT\\ &dG=v~dp-S~dT\end{aligned}\]

on tire : \[S=-\Big(\frac{\partial F}{\partial T}\Big)_v\quad;\quad S=-\Big(\frac{\partial G}{\partial T}\Big)_p\]

qui, associées respectivement à : \[\Big(\frac{\partial S}{\partial T}\Big)_v=\frac{C_v}{T}\quad;\quad \Big(\frac{\partial S}{\partial T}\Big)_p=\frac{C_p}{T}\]

conduisent à : \[C_v=-T~\Big(\frac{\partial^2F}{\partial T^2}\Big)_v\quad;\quad C_p=-T~\Big(\frac{\partial^2G}{\partial T^2}\Big)_p\]