1. Généralités
En transmission numérique, l’information utile est véhiculée sous forme numérique, c’est-à-dire une suite aléatoire de 0 et de 1 provenant soit du traitement de l’information analogique (échantillonnage, quantification, codage, etc.), soit directement d’un système numérique (ordinateur).
La transmission d’une information numérique par voie électromagnétique nécessite une adaptation du signal à transmettre au canal de transmission dont on dispose.
Ce canal de transmission sera par exemple un câble, un faisceau hertzien, une liaison par satellite. Il se comporte comme un filtre passe-bas ou passe-bande.
Deux types de transmission sont possibles :
-
Transmission en bande de base : le signal numérique est émis sans transposition de fréquence ;
-
Transmission sur fréquence porteuse : le signal numérique est transposé autour d’une fréquence située dans la bande passante du canal de transmission.
2. Les signaux numériques
2.1. Source numérique
On appelle source numérique (ou source binaire) tout ce qui délivre une succession d’états binaires ou logiques, c’est-à-dire une suite aléatoire de 0 et de 1. Chaque état binaire est appelé bit et porte un élément unitaire d’information.
C’est cette suite, représentative du signal à transmettre, qu’il faut envoyer vers le destinataire : on a alors recours à un codage électrique qui associe à ces états logiques des états électriques qui seront effectivement transmis sur le support de transmission choisi.
2.2. Débit
La source numérique fournit une suite d’états logiques durant chaque temps élémentaire \(T\) (exprimé en secondes).
Le débit correspond au nombre d’états logiques fournis par la source pendant une seconde.
 On pourrait dire, que pendant le temps \(T\), la source dite élémentaire fournit un seul état logique, donc : \[D=\frac{1}{T}\]
On pourrait dire, que pendant le temps \(T\), la source dite élémentaire fournit un seul état logique, donc : \[D=\frac{1}{T}\]
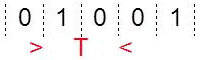 Mais en pratique, les informations numériques sont généralement transmises au dispositif de transmission en parallèle par groupes de \(N\) bits : 8, 16, 32, 64, voire plus. La source fournit donc dans la réalité \(N\) états logiques, donc en toute rigueur : \[D=\frac{N}{T}\]
Mais en pratique, les informations numériques sont généralement transmises au dispositif de transmission en parallèle par groupes de \(N\) bits : 8, 16, 32, 64, voire plus. La source fournit donc dans la réalité \(N\) états logiques, donc en toute rigueur : \[D=\frac{N}{T}\]
Ce débit s’exprime en bits par seconde (symbole bits/s ou bps). Il caractérise la capacité d’une transmission en indiquant le nombre d’états logiques, donc la quantité d’informations, qu’il peut transmettre par seconde.
NB : Le débit réel est toujours inférieur, car il faut ajouter aux informations utiles des éléments de protocoles qui permettent de décoder, synchroniser ou vérifier les données transmises.
2.3. Rapidité de modulation
 Pour transmettre ces états logiques, on les code en leur associant un niveau de tension, et ce sont les états électriques qui seront effectivement transmis sur le support de transmission choisi.
Pour transmettre ces états logiques, on les code en leur associant un niveau de tension, et ce sont les états électriques qui seront effectivement transmis sur le support de transmission choisi.
Après codage électrique, on a par exemple à transmettre des états électriques de durée élémentaire \(\tau\), parfois appelé moment.
La rapidité de modulation correspond au nombre d’états électriques transmis pendant une seconde, exprimée en bauds (symbole Bd), est : \[R=\frac{1}{\tau}\]
Elle est liée au support de transmission choisi.
Sur un support de transmission imposé, on ne peut pas transmettre des états électriques issus des états logiques par l’intermédiaire de n’importe quel codage électrique sous peine de ne pouvoir reconnaître en réception l’information que l’on a émise.
2.4. Valence
La valence \(v\) d’un signal correspond au nombre d’états logiques différents qu’il peut prendre.
Le nombre de d’informations binaires transmissibles par moment élémentaire du signal est inférieur ou égal au logarithme en base 2 de sa valence. Les trois paramètres, débit, rapidité de modulation et valence sont donc liés par la relation : \[D\leq R~\log_2(v)\]
En remarquera que la valeur du débit (en bits par seconde) et celle de la rapidité de modulation (en bauds) sont égales quand le signal est bivalent, c’est-à-dire à deux états seulement.
2.5. Exemples
Code NRZ (Non retour à zéro)
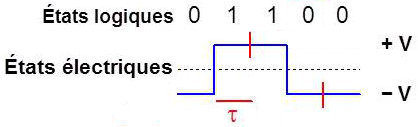 2 niveaux de tension :
2 niveaux de tension :
\[\begin{aligned} &0\quad\rightarrow -~V~(\text{durée}~\tau)\\ &1\quad\rightarrow +~V~(\text{durée}~\tau)\end{aligned}\]
Un bit d’information est transmis pendant chaque moment : \[v=2 \quad;\quad D=R\]
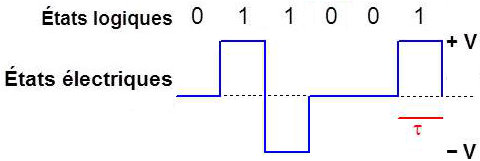 Code bipolaire d’ordre 1
Code bipolaire d’ordre 1
3 niveaux de tension :
\[\begin{aligned} &0\quad\rightarrow 0~V\\ &1\quad\rightarrow \pm~V~\quad\text{alternativement}\end{aligned}\]
Si la valeur 1 a été matérialisée par (+ V), elle le sera par (- V) la fois suivante et ainsi de suite.
Un bit d’information est transmis pendant chaque moment : \[v=3 \quad;\quad D=R\]
Le débit et la rapidité de modulation sont identiques dans les deux codes précédents.
Code à 4 niveaux
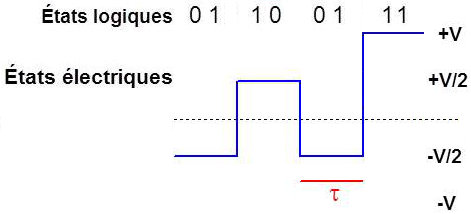 4 niveaux de tension :
4 niveaux de tension :
\[\begin{aligned} &00\quad\rightarrow~-V\\ &01\quad\rightarrow~-\frac{V}{2}\\ &10\quad\rightarrow~+\frac{V}{2}\\ &11\quad\rightarrow~+V\end{aligned}\]
Deux bits d’information sont transmis pendant chaque moment : \[v=4 \quad;\quad D=2~R\]
Tableau résumé
\[\begin{aligned} &\text{Codage}& &\text{Valence}& &\text{Débit}\\ &NRZ& &v=2& &D=R& &D=R~log_2(v)\\ &Bipolaire& &v=3& &D=R& &D<R~log_2(v)\\ &4~niveaux& &v=4& &D=2~R& &D=R~log_2(v)\end{aligned}\]
Lorsque \(D<R~log_2(V)\), on dit qu’il y a redondance : le débit, c’est-à-dire le nombre d’informations transmises pendant l’unité de temps, est inférieur au débit maximal \(R~log_2(v)\) que l’on pourrait théoriquement utiliser.
Dans l’exemple du code NRZ et du code à 4 niveaux, \(D=R~log_2(V)\) : le débit utilisé est le débit maximal ; on ne pourrait pas transmettre plus d’informations.
Dans l’exemple du code bipolaire d’ordre 1, \(D<R~log_2(V)\) avec 3 niveaux électriques. On pourrait passer plus d’informations, le maximum étant atteint avec \(D=R~log_2(3)\). On ne le fait pas ici car effectivement on utilise un niveau de tension qui n’apporte pas d’informations supplémentaires, le niveau (–V) étant représentatif des mêmes informations 1 que le niveau (+V). Nous verrons plus loin que cet alternat de codage des 1 est néanmoins utile pour certaines raisons.
3. Représentation temporelle des signaux
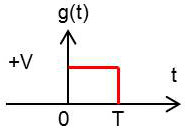
Le signal électrique à transmettre s’écrit sous la forme d’une suite : \[x(t)=\sum_{k=-\infty}^{k=+\infty}a_k~g(t-k~\tau)\]
-
\(g(t)\) : formant utilisé pour la transmission (créneau, carré, forme en cloche etc.)
-
\(a_k\) : poids associé au codage
Exemples :
-
Code NRZ : \(a_k=-1~ou~+1\)
-
Code bipolaire 1 : \(a_k=-1~ou~0~ou~+1\)
-
Code à 4 niveaux : \(a_k=-2~ou~-1~ou~0~ou~+1~ou~+2\)
4. Représentation fréquentielle ou spectrale
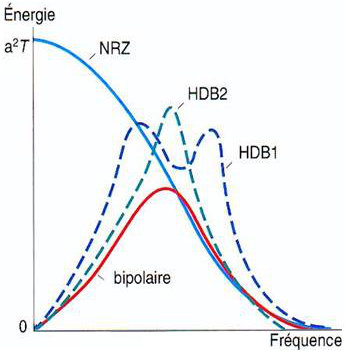 La connaissance de la forme du spectre d’énergie (ou de puissance) est intéressante. Elle montre, suivant le code choisi, où se trouve la plus grande répartition de l’énergie. C’est cette bande de fréquence qu’il faut donc privilégier.
La connaissance de la forme du spectre d’énergie (ou de puissance) est intéressante. Elle montre, suivant le code choisi, où se trouve la plus grande répartition de l’énergie. C’est cette bande de fréquence qu’il faut donc privilégier.
Il serait par exemple déconseillé d’introduire un support se comportant comme un filtre passe-bas pour un code bipolaire puisque le maximum d’énergie se trouve à une fréquence relativement élevée. Un filtre de type passe-bande centré sur cette fréquence correspondrait à l’utilisation optimale du spectre.
Un signal numérique porteur d’information est un signal aléatoire donc de puissance finie. On s’intéressera au calcul de sa DSP (densité spectrale de puissance).
4.1. Calcul de la DSP. Formule de Bennett
La DSP du signal \(x(t\)) est donnée par : \[S_{xx}(f)=\mathcal{F}[R_{xx}(\tau)]=\mathcal{F}\{E[x(t)~x(t-\tau)]\}\]
La suite \(a_k~;~k\in ]\infty~,~+\infty[\) est supposée stationnaire, c’est-à-dire que :
\[\begin{aligned} &E[a_k]=\text{cte}\\ &E[a_k~a_{k+n}]=R_a(n)~~\text{ne dépend que de n}\end{aligned}\]
Le calcul de la fonction d’autocorrélation étant relativement complexe, nous la résumerons et aboutirons à la formule générale de Bennett qui est appliquée systématiquement au calcul des DSP des différents codes.
Formule de Bennett
On introduit une variable aléatoire \(\Phi\) uniformément répartie dans \([0,\tau]\).
Elle correspond à l’aléa de démarrage du signal électrique :
\[\begin{aligned} &R_{xx}(\tau)=E\{x(t)~x(t-\tau)\}\\ &R_{xx}(\tau)=E\left\{\sum_k a_k~g(t-kT-\Phi)\times\sum_la_l~g(t-l~T-\tau-\Phi)\right\}\end{aligned}\]
On fait l’hypothèse que les deux processus \(a\) et \(\Phi\) sont indépendants. On utilise également les propriétés de linéarité qui permettent la permutation des opérateurs Espérance mathématique E et Intégrale. Le calcul intégral conduit ainsi à l’expression : \[R_{xx}(\tau)=\left\{\frac{m_a^2}{T}~R_{gg}(\tau)\star\text{Ш}_{(T)}\right\}+\left\{\sum_n\frac{R_a(n)-m_a^2}{T}~R_{gg}(\tau)\star\delta(t-n~T)\right\}\]
En passant ensuite à la transformée de Fourier : \[S_{xx}(f)=S_{gg}(f)~\left\{\frac{m_a^2}{T^2}~\text{Ш}_{(1/T)}+\frac{\sigma_a^2}{T}+\sum_{n=1}^{\infty}\frac{R_a(n)-m_a^2}{T}~2\cos(2\pi~f~n~T)\right\}\]
Le premier terme est la composante discrète du signal et le deuxième la composante continue.
Un cas intéressant est celui où les symboles \(a_k\) sont indépendants (codes binaires) et stationnaires : \[R_a(n)=E[a_k~a_{k+n}]=E[a_k]~E[a_{k+n}]\]
La formule de Bennett est alors très simplifiée : \[S_{xx}(f)=S_{gg}(f)~\left\{\frac{m_a^2}{T^2}~\text{Ш}_{(1/T)}+\frac{\sigma_a^2}{T}\right\}\]
4.2. Application au code binaire NRZ
 Les échantillons \(a_k\) peuvent prendre les valeurs \(0\) ou \(1\) avec la même probabilité 1/2.
Les échantillons \(a_k\) peuvent prendre les valeurs \(0\) ou \(1\) avec la même probabilité 1/2.
Pour les calculs suivants, nous considèrerons une source élémentaire (1 bit à chaque intervalle \(T\)) et la réalisation suivante :
\[\begin{aligned} 0~&\rightarrow~0~V\\ 1~&\rightarrow~+V\end{aligned}\]
Les symboles étant indépendants, nous appliquerons la formule de Bennett simplifiée.
Il faut calculer \(S_{gg}(f),~m_a^2,~\sigma_a^2\).
\(g(t)\) est la fonction porte, donc le signal est d’énergie finie. On a donc : \[S_{gg}(f)=|G(f)|=V^2~T^2~\operatorname{sinc}^2(\pi~f~t)\]
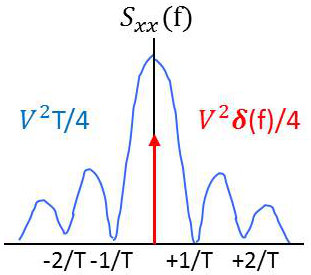 \[\begin{aligned} m_a&=E[a_k]=0\times\frac{1}{2}+1\times\frac{1}{2}=\frac{1}{2}\quad\Rightarrow\quad m_a^2=\frac{1}{4}\\ \sigma_a^2&=E[a_k^2]-m_a^2=\Big(0^2\times\frac{1}{2}+1^2\times\frac{1}{2}\Big)-\frac{1}{4}=\frac{1}{4}\\ S_{xx}(f)&=V^2~T^2~\operatorname{sinc}^2(\pi~f~T)\left\{\frac{1}{4~T^2}~\text{Ш}_{(1/T)}+\frac{1}{4~T}\right\}\\ S_{xx}(f)&=\frac{V^2~T^2}{4}~\operatorname{sinc}^2(\pi~f~T)\left\{\frac{1}{T}~\text{Ш}_{(1/T)}+1\right\}\\ S_{xx}(f)&=\frac{V^2~T^2}{4}~\operatorname{sinc}^2(\pi~f~T)\left\{\frac{1}{T}\sum_{n=-\infty}^{n=+\infty}\delta(f-\frac{n}{T})+1\right\}\end{aligned}\]
\[\begin{aligned} m_a&=E[a_k]=0\times\frac{1}{2}+1\times\frac{1}{2}=\frac{1}{2}\quad\Rightarrow\quad m_a^2=\frac{1}{4}\\ \sigma_a^2&=E[a_k^2]-m_a^2=\Big(0^2\times\frac{1}{2}+1^2\times\frac{1}{2}\Big)-\frac{1}{4}=\frac{1}{4}\\ S_{xx}(f)&=V^2~T^2~\operatorname{sinc}^2(\pi~f~T)\left\{\frac{1}{4~T^2}~\text{Ш}_{(1/T)}+\frac{1}{4~T}\right\}\\ S_{xx}(f)&=\frac{V^2~T^2}{4}~\operatorname{sinc}^2(\pi~f~T)\left\{\frac{1}{T}~\text{Ш}_{(1/T)}+1\right\}\\ S_{xx}(f)&=\frac{V^2~T^2}{4}~\operatorname{sinc}^2(\pi~f~T)\left\{\frac{1}{T}\sum_{n=-\infty}^{n=+\infty}\delta(f-\frac{n}{T})+1\right\}\end{aligned}\]
4.3. Application au code bipolaire NRZ d’ordre 1
La différence avec le code précédent est la suivante : 0 est réalisé par (0 V), mais 1 est réalisé par (+V) et (–V) alternativement. C’est-à-dire que \(a_k\) peut prendre trois valeurs non indépendantes 0, + 1 et – 1, car un +1 suit un -1 et réciproquement.
On utilisera donc cette fois la formule complète de Bennett. Le formant est le même que celui du code NRZ :
\[\begin{aligned} g(t)&=V~\Pi_T\Big(t-\frac{T}{2}\Big)\\ S_{gg}(f)&=V^2~T^2~\operatorname{sinc}^2(\pi~f~t)\end{aligned}\]
Il reste à calculer : \(m_a^2,~\sigma_a^2,~R_a(n)=E(a_k~a_{k+n})\) :
\[\begin{aligned} E[a_k~a_{k+n}]&=\sum_i\sum_j\alpha_i~\alpha_j~p_{ij}\\ \{\alpha_i\}_i&\quad\text{réalisations possibles de}~a_k\\ \{\alpha_j\}_j&\quad\text{réalisations possibles de}~a_{k+n}\\ p_{ij}&=\operatorname{prob}(a_k=\alpha_i~,~a_{k+n}=\alpha_j)\\ p_{ij}&=\operatorname{prob}(a_k=\alpha_i)\times\operatorname{prob}(a_{k+n}=\alpha_j~/~a_k=\alpha_i)\\ p_{ij}&=p_i~[P_{j/i}]_n\qquad~\text{notation simplifiée}\end{aligned}\]
Alors : \[E[a_k~a_{k+n}]=\sum_i\sum_j\alpha_i~\alpha_j~p_i~[P_{j/i}]_n\]
Les termes \((P_{j/i})_n\) sont donnés par la matrice de Markow \(M^n\) qui fournit les probabilités de passage d’un état \(\alpha_i\) à un instant \(t\) à un état \(\alpha_j\) à l’instant \(t + nT\).
Il va falloir écrire la matrice de Markow qui fournit les probabilités de passage entre deux instants consécutifs \(t\) et \(t + T\), puis l’élever à la puissance n.
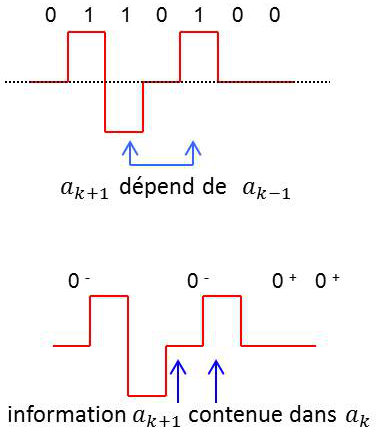 Pour pouvoir utiliser le processus de Markov, il faut que le code corresponde à une chaîne de Markov, c’est-à-dire que l’état du système à un instant donné ne dépende que de l’état précédent.
Pour pouvoir utiliser le processus de Markov, il faut que le code corresponde à une chaîne de Markov, c’est-à-dire que l’état du système à un instant donné ne dépende que de l’état précédent.
Autrement dit, il faut que \(a_{k+1}\) ne dépende que de \(a_k\). Or la construction du code bipolaire fait que \(a_{k+1}\) ne dépend pas que de \(a_k\) (alternance des 1).
Pour remédier à cet inconvénient, on va procéder à un dédoublement des 0 en adoptant la règle suivante :
-
\(0^+\) si le 0 suit un +1
-
\(0^-\) si le 0 suit un -1
Le système répond alors au processus de Markov.
Il reste ensuite à écrire la matrice \(M\), puis à calculer \(M^n\) qui permettra de générer les \([P_{j/i)}]_n\) intervenant dans \(R^a(n)\).
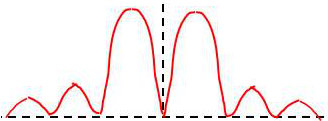 On trouve que la densité spectrale de puissance \(S_{xx}(f)\) a l’allure ci-contre.
On trouve que la densité spectrale de puissance \(S_{xx}(f)\) a l’allure ci-contre.
On constate que la bipolarité (alternat des 1) a entraîné un déplacement de la répartition spectrale du signal vers les fréquences positives.

