1. Introduction

On dit que la transmission s’effectue sur fréquence porteuse quand on transpose le spectre du signal numérique à transmettre (spectre qui se situait en bande de base à l’origine) autour d’une fréquence $f_0$ située dans la bande passante du canal de transmission.

Cette transposition est réalisée par une modulation qui peut être soit une modulation d’amplitude, soit une modulation de phase. C’est de cette dernière dont nous parlerons à présent, car elle est la plus utilisée.

2. Modulation de phase cohérente à deux états

La modulation de phase numérique cohérente, en anglais phase-shift keying (PSK), nécessite :

• un signal porteur (ou porteuse) de la forme $A~\cos(2\pi~f_0~t+\varphi_0)$ ;

• un signal modulant $m(t)$ qui est le signal numérique à transmettre.

Soit le signal modulé : $$s(t)=A~\cos(2\pi~f_0~t+\varphi_0+\varphi)\qquad\varphi~\text{ne dépendant que de}~m(t)$$

La modulation intervient au niveau de la phase porteuse.

La correspondance entre $\varphi$ et $m(t)$ est représenté par le tableau suivant : $$\begin{matrix} m(t)& &\varphi\\ 0& &0\\ 1& &\pi \end{matrix}$$

On sépare ces états de phase le plus possible de façon à ce que, en présence de bruit, le récepteur fasse une estimation la moins erronée possible.

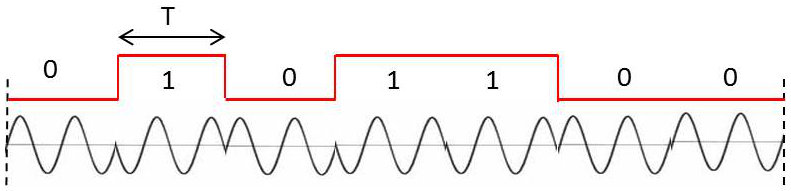Nous représentons ci-contre le signal $m(t)$ en créneau qui est le message à transmettre et (en-dessous) le signal $s(t)$ qui est le signal modulé transmis.

Dans ce cas, nous avons choisi $D=R$ :

$$\begin{aligned} &s(t)=A~\cos(2\pi~f_0~t+\varphi_0+\varphi)\qquad\varphi=0\text{ ou }\pi\\ &s(t)=\pm A~\cos(2\pi~f_0~t+\varphi_0)\end{aligned}$$

On voit que la modulation MDP-2 se ramène à une modulation d’amplitude, car c’est l’amplitude de la porteuse qui se trouve multipliée par $\pm 1$ selon l’information à véhiculer.

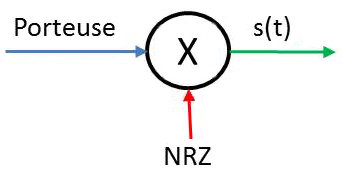Pour effectuer cette modulation, on utilise un modulateur en anneau, appelé aussi multiplieur, symbolisé par $\otimes$.

On sait (cf. communications analogiques) que lorsque l’on effectue une modulation d’amplitude avec un signal modulant aléatoire (ce qui est la cas pour un signal numérique), la densité spectrale de puissance de ce signal est transposée autour de la fréquence porteuse.

Le signal NRZ est codé entre $\pm V$.

On aura la correspondance : $$0~\rightarrow +V\quad;\quad 1~\rightarrow +V$$

Pour démoduler, il suffit de multiplier une seconde fois par la porteuse (démodulation cohérente).

En effet : $$s(t)\times\cos(2\pi~f_0~t+\varphi_0)=\frac{A^2}{2}~\cos(\varphi)\big\{1-\cos(4\pi~f_0~t+\varphi_0)\big\}$$

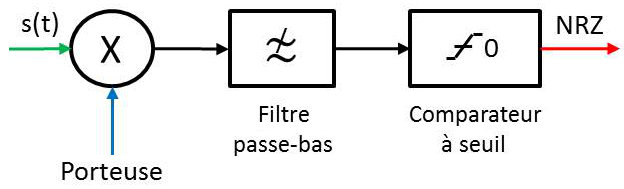Le cosinus extrême est un terme (haute fréquence) autour de la fréquence $2~f_0$. Le terme $A^2~\cos(\varphi/2)$ est préservé par filtrage passe-bas.

Une détection de signe suffit pour estimer la valeur des symboles émis $0~,~1$.

Le gros problème de cette démodulation cohérente réside dans la nécessité de récupérer la porteuse en réception. On la récupère en multipliant le signal reçu par lui-même de façon à éliminer la modulation, puis un divisant par deux la fréquence obtenue.

$$\begin{aligned} s(t)&=A~\cos(2\pi~f_0~t+\varphi_0+\varphi) &&\varphi=0\text{ ou }\pi\\ s^2(t)&=\frac{A^2}{2}~\cos(\varphi)\big\{1+\cos(4\pi~f_0~t+2\varphi_0+2~\varphi)\big\} &&2~\varphi=0\text{ ou }2\pi\end{aligned}$$

On voit avec le terme $2\varphi$ que la modulation a été effectivement supprimée.

On peut s’affranchir de la nécessité de disposer de la porteuse en réception en utilisant une autre démodulation, la MDP-2 différentielle décrite ci-après, mais dont les performances sont moins bonnes.

3. Modulation de phase différentielle à deux états

La correspondance entre $\varphi$ et $m(t)$ pendant un intervalle de durée $T$ est fonction cette fois de la valeur précédente :
 

$$\begin{matrix} m(t)~\text{à}~n~T& &\varphi_n~\text{à}~n~T\\ \qquad\\ 0& &\varphi_n=\varphi_{n-1}\\ 1& &\varphi_n=\varphi_{n-1}+\pi \end{matrix}$$

Cette modulation différentielle est pratiquement impossible à réaliser directement, car elle nécessite un effet de mémoire (on doit garder la phase en mémoire pendant le temps T).

Mais on peut construire en appliquant la modulation cohérente à un code dit NRZ différentiel ou NRZ par transition issu directement du signal numérique à transmettre.

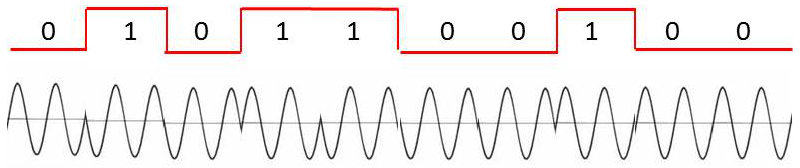
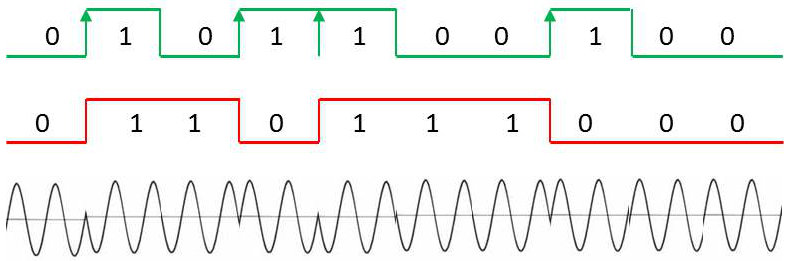Le premier diagramme ci-contre représente directement le signal de message.

Le NRZ différentiel se construit à partir du code $m(t)$. Il s’en déduit en effectuant une transition d’état à chaque front montant de $m(t)$.

Il suffit d’appliquer ensuite à ce NRZ différentiel la démodulation cohérente et on retrouve le signal $s(t)$ cherché.

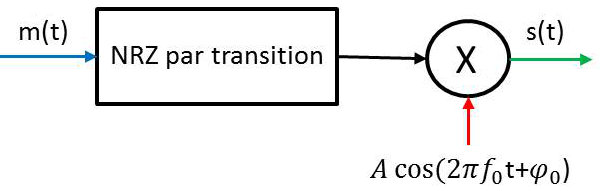Pour effectuer une modulation différentielle, on utilise la technique de la modulation cohérente à partir d’un code intermédiaire, le code différentiel.

Le signal NRZ par transition a même densité spectrale de puissance que le signal numérique à transmettre.

On se ramène, comme dans le cas précédent, à une modulation d’amplitude et on peut dire que la DSP du signal à émettre est translatée autour de $f_0$.

L’intérêt de cette modulation différentielle réside dans la démodulation où l’on n’aura pas besoin de la porteuse.

En effet, il suffit de retarder $s(t)$ de $T$ à l’aide d’une ligne à retard (LAR) et de multiplier ce nouveau signal par $s(t)$.
 

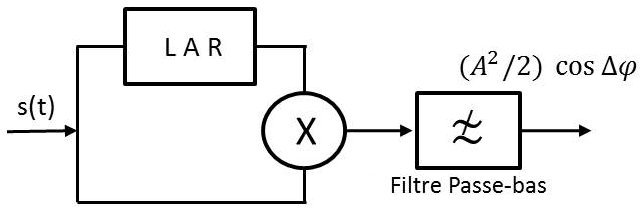$$\begin{aligned} &\text{Instant }(n-1)~T &&\text{signal} &&A~\cos(2\pi~f_0~t+\varphi_0) \\ &\text{Instant }n~T &&\text{signal} &&A~\cos(2\pi~f_0~t+\varphi_0+\Delta\varphi)\end{aligned}$$

Le saut de phase $\Delta\varphi$ , porteur de l’information a pour valeurs soit $0$, soit $\pi$

À la sortie du multiplieur, on aura : $$s^2(t)=\frac{A^2}{2}\cos(\varphi)~\big\{\cos(4\pi~f_0~t+2\varphi_0+\Delta\varphi)+\cos(\Delta\varphi)\big\}$$

Le premier cosinus correspond à un signal H centré sur $2~f_0$ qui sera éliminé par filtrage passe-bas.

En utilisant un comparateur à seuil (seuil à zéro), on pourra estimer la valeur de $\Delta\varphi$, donc du signal numérique $b(t$) que l’on a émis.

4. Modulation de phase à n états MDP-N

$N$ correspond au nombre d’états de phase possibles, c’est-à-dire à la valence.

Pour la MDP-2, on a $v = 2$ et $D = R$.

4.1. Modulation MDP-4 ou MDPQ

La modulation de phase en quadrature va utiliser 4 états de phase que l’on va choisir aussi disjoints que possible de façon à ce que, en présence de bruit, le récepteur fasse une estimation la moins erronée possible. Par exemple : $$\begin{matrix} 00& & &\varphi=0\\ 01& & &\varphi=\pi/2\\ 10& & &\varphi=\pi\\ 11& & &\varphi=3\pi/2 \end{matrix}$$

4.2. Modulation MDP-8

Avec la MDP-8, nous aurons donc 8 états de phase : $$\begin{matrix} 000& & &\varphi=0\\ 001& & &\varphi=\pi/4\\ 010& & &\varphi=\pi/2\\ ---& & &---\\ 111& & &\varphi=7\pi/4 \end{matrix}$$

Pour des raisons de bruit et des problèmes de détection, il est difficile de dépasser 8 états de phase.

Ces modulations MDP-N, $N > 2$, bien que plus intéressantes en ce qui concerne la détection, présentent un autre intérêt : sur support de transmission identique (c’est-à-dire à rapidité de modulation ou à bande passante fixée), on peut transmettre plus d’informations.

5. Probabilité d’erreur

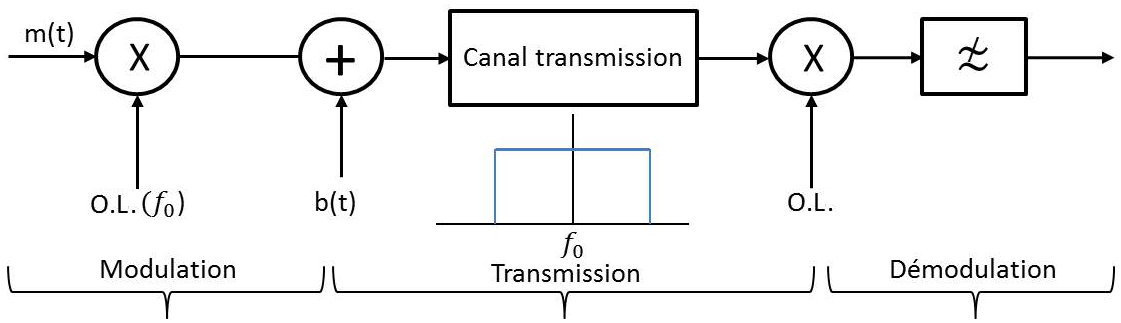Le canal de transmission réel utilisé en modulation cohérente peut être schématisé par le schéma ci-contre.

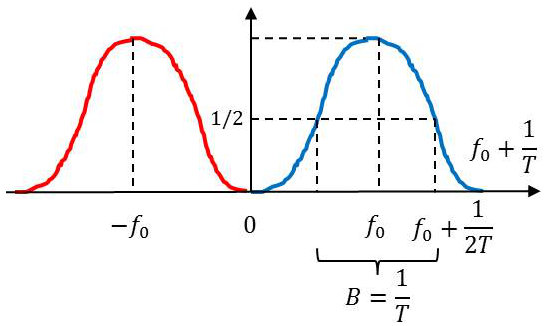
La densité spectrale de puissance de $s(t)$, centrée autour de la fréquence porteuse $f_0$, a un support infini.

Le canal de transmission, symbolisé par un filtre passe-bande, introduit une déformation du signal $s(t)$ qui se manifeste par un effet de traînage (comme on l’a vu en transmission en bande de base), d’où résultera une interférence inter symboles.

Pour supprimer cette interférence, la condition de Nyquist doit être réalisée.

Si $R$ est la rapidité de modulation du signal modulé (en MDP-2, on a $R = 1/T$), la fonction de transfert du canal de transmission doit être représentée comme le montre la figure contre.

En transmission sur fréquence porteuse comme en transmission en bande de base, rapidité de modulation et support de transmission sont liés.

Après démodulation, il faut utiliser comme on l’a vu, un comparateur à seuil (le seuil étant fixé à zéro) qui recevra un signal de la forme :

$$\begin{aligned} &\text{MDP-2 cohérente :} &&\frac{A^2}{2}~\cos(\varphi)\\ &\text{MDP-2 différentielle :} &&\frac{A^2}{2}~\cos(\Delta\varphi)\end{aligned}$$

Les calculs de probabilité d’erreur sont identiques à ceux abordés en transmission en bande de base.