1. Contexte

Ce court chapitre sur les modulations d’amplitude en quadrature (Quadrature Amplitude Modulation = QAM) se présente comme un complément aux chapitres précédents, à titre d’information cependant nécessaire.

Le format de modulation QAM est étudié très sérieusement dans le domaine des télécommunications par satellite ou par fibre optique afin de répondre aux besoins exprimés par une augmentation de plus en plus importante du débit.

Il a également été adopté pour la télévision numérique terrestre (TNT). Pour information, la France a adopté le format 64QAM, correspondant à 6 bits par symbole.

2. Principe de la MAQ - QAM

La QAM (modulation d’amplitude en quadrature) résulte de la composition de deux fréquences porteuses sinusoïdales déphasées l’une de l’autre de \(\pi/2\).

Du fait de cette orthogonalité, la détection (démodulation) s’en trouve facilitée.

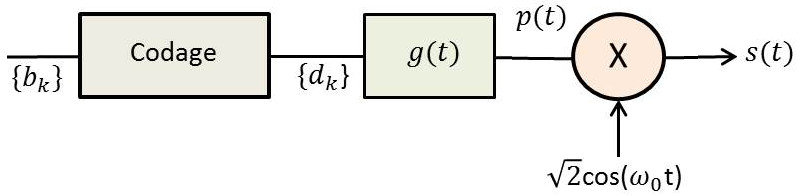Rappelons le schéma de principe de la modulation d’impulsion en amplitude (MIA) et l’expression mathématique correspondante : \[s(t)=\sum_k d_k~g(t-kT_s)~\sqrt{2}~\cos(\omega_0t+\varphi)\]

Le facteur \(\sqrt{2}\) est souvent introduit pour une commodité (normalisation) dans les calculs de puissance (présence du cosinus).

Un autre signal numérique qui module un sinus à la même fréquence peut être ajouté au cosinus, ces deux signaux occupant le même spectre et sont facilement séparables à la démodulation (orthogonalité des porteuses).

Cette modulation des deux porteuses en quadrature (QAM) a pour expression mathématique : \[p(t)~\sqrt{2}~\cos(\omega_0t+\varphi)-q(t)~\sqrt{2}~\sin(\omega_0t+\varphi)\]

En ayant posé : \[p(t)=\sum_k d_{pk}~g(t-kT_s)~\sqrt{2}\quad;\quad q(t)=\sum_k d_{qk}~g(t-kT_s)~\sqrt{2}\]

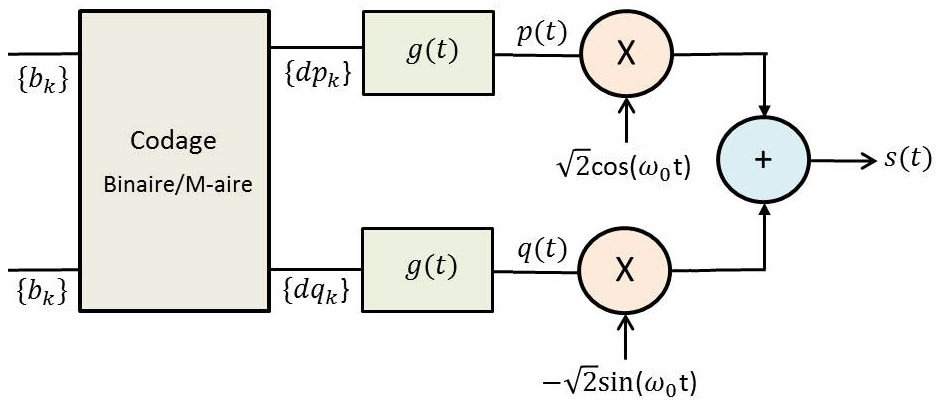Avec sa voie en sinus, la modulation QAM permet de passer deux fois plus de données que la la MIA classique pour une même occupation spectrale. Son efficacité spectrale a été doublée.

Rappelons que l’efficacité spectrale \(\eta\) est définie comme le rapport du débit d’information binaire transmis par la modulation à la largeur de bande utilisée : \(\eta=D_b~/~W\).

3. Un exemple simple de modulation QAM

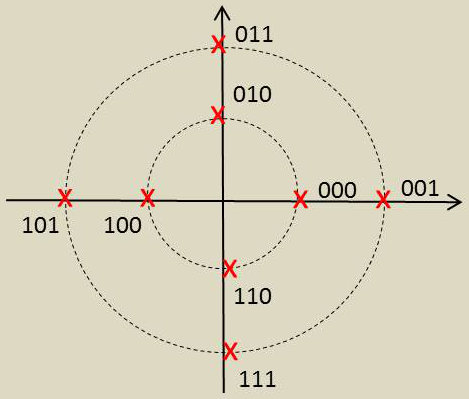Exemple de 8QAM ou 8 états (source Wikipedia).

On fait donc l’hypothèse de 3 bits transmis par symbole, soit \(2^3=8\) combinaisons en faisant l’hypothèse de deux amplitudes différentes (voir le tableau ci-dessous et les constellations correspondantes). \[\begin{matrix} &\text{Groupe bits}& &\text{Amplitude}& &\text{Déphasage}\\ &000& &0.5& &0\\ &001& &1& &0\\ &010& &0.5& &\pi/2\\ &011& &1& &\pi/2\\ &100& &0.5& &\pi\\ &101& &1& &\pi\\ &110& &0.5& &3\pi/2\\ &111& &1.& &3\pi/2 \end{matrix}\]

Considérons par exemple la séquence suivante : 100 | 001 | 011 | 110.

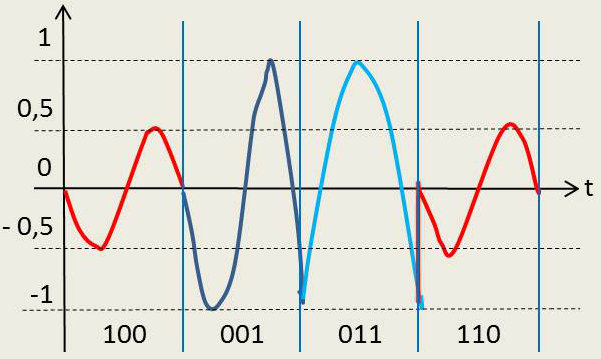Il lui correspond une représentation temporelle de la figure ci-contre.