1. Rappels liés au vecteur d’onde

Le chapitre sur les équations de Maxwell est supposé acquis.

Une onde (vecteur d’onde \(\overrightarrow{k}\)) se réfléchit sur un conducteur selon la loi de Descartes : \[\overrightarrow{k'}_t=\overrightarrow{k}_t\quad;\quad\overrightarrow{k'}_n=-\overrightarrow{k}_n\]

Le champ électrique réfléchi est le transformé de l’incident par rotation \([\pi]\) autour de la normale. Le champ magnétique réfléchi est le transformé de l’incident dans la rotation qui amène \(\overrightarrow{k}\) sur \(-\overrightarrow{k}\).

Le champ électrique total tangentiel et le champ magnétique total normal sont nuls sur le conducteur parfait, la nullité de \(\overrightarrow{H}_n\) résulte de celle de \(\overrightarrow{E}_t\).

Le champ électromagnétique incident interfère avec le champ réfléchi pour donner un champ :

• de périodicité normale : \[\frac{1}{\bar{k}_n}=\frac{2\pi}{k_n}\]

• de périodicité tangentielle : \[\frac{1}{\bar{k}_t}=\frac{2\pi}{k_t}\]

Remarquer la notation \(\bar{k}\) (analogie avec le barre de la mécanique quantique).

Ce champ glisse le long du miroir à la vitesse (de phase) : \[\frac{\nu}{\bar{k}_t}=\frac{\omega}{k_t}=\frac{c'}{\sin\theta}\]

• \(c'\) : vitesse de l’onde dans le diélectrique

• \(\theta\) : angle d’incidence avec : \(\sin\theta=\cfrac{k_t}{k}\)

2. Réflexion d’une onde entre deux miroirs parallèles

2.1. Les paramètres

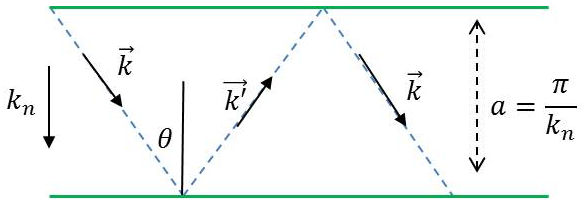Disposons un second plan parfaitement conducteur à une distance multiple de la demi-périodicité normale (\(\pi/k_n\)).

Les conditions aux limites se trouvent à nouveau satisfaites sur le deuxième plan et le signal électromagnétique se propage entre les deux plans par réflexions successives :

\[\begin{aligned} &a=\frac{\pi}{k_n}\quad\text{ou}\quad\bar{k}=\frac{1}{2~a} &&\text{premier mode}\\ &\bar{k}_n=\frac{p}{2~a} &&\text{deuxième mode}\end{aligned}\]

Le rayon avance parallèlement aux miroirs à la vitesse \(c'~\sin\theta\) : c’est la vitesse de groupe.

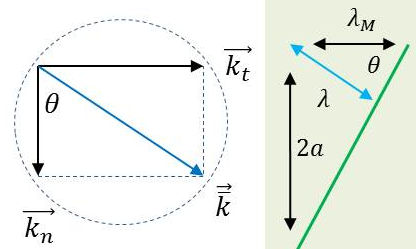En remarquant la position des vecteurs par rapport à un cercle, on peut faire intervenir une inversion de pôle \(O\) et de puissance 1. D’où une représentation des plans d’une onde (ici le premier mode) :

\[\begin{aligned} &\bar{k}_n=\frac{1}{2~a}~\bar{k}=\frac{1}{\lambda}\\ &\bar{k}_t=\frac{1}{\lambda_M}\end{aligned}\]

2.2. Vitesse de phase et vitesse de groupe

Soit \(c'\) la vitesse de l’onde dans le diélectrique du guide : \[c'=\frac{1}{\sqrt{\mu~\varepsilon}}\]

Si la pulsation est donnée, il vient : \[k=\frac{\omega}{c'}=\frac{2\pi}{\lambda}\]

La vitesse de phase à laquelle glisse le champ parallèlement aux miroirs est : \[v_{\varphi}=\frac{\omega}{k_t}=\frac{c'}{\sin\theta}\qquad\qquad\theta~\text{: angle d'incidence}\]

Par ailleurs :

\[\begin{aligned} a&=p~\frac{\pi}{k_n}=p~\frac{\pi}{k~\cos\theta}=\frac{p}{2~\bar{k}~\cos\theta}=\frac{\lambda~p}{2~\cos\theta}\\ \sin\theta&=\frac{\bar{k}_t}{\bar{k}}=\pm~\sqrt{1-\frac{p^2}{4~a^2~\bar{k}^2}}=\pm~\sqrt{1-\frac{p^2~\lambda^2}{4~a^2}}\end{aligned}\]

On obtient alors pour la vitesse de phase : \[v_{\varphi}=\frac{c'}{\sqrt{1-\cfrac{p^2~\lambda^2}{4~a^2}}}=\frac{c'}{\sqrt{1-\cfrac{p^2~\pi^2~c'^2}{a^2~\omega^2}}}\]

\(\qquad p\) : ordre du mode

La période spatiale, parallèlement au miroir est : \[\lambda_M=\frac{2\pi}{k_t}=\frac{1}{\bar{k}_t}=\frac{\lambda}{\sin\theta}=\frac{2~a}{p}~\cot\theta\]

La dispersion est donnée par : \[k_t=\frac{\omega}{v_{\varphi}}=\frac{\omega}{c'}~\sqrt{1-\cfrac{p^2~\pi^2~c'^2}{a^2~\omega^2}}=\sqrt{\frac{\omega^2}{c'^2}-\frac{p^2~\pi^2}{a^2}}\]

D’où la vitesse de groupe (\(v_g\)) : \[\frac{1}{v_g}=\frac{dk_t}{d\omega}=\frac{\cfrac{2~\omega}{c'^2}}{2~\sqrt{\cfrac{\omega^2}{c'^2}-\cfrac{p^2~\pi^2}{a^2}}} =\frac{\omega}{c'^2~k_t}=\frac{v_{\varphi}}{c'^2}\]

On a donc : \[v_g~v_{\varphi}=c'^2\]

Ou encore : \[v_{\varphi}=\frac{c'}{\sin\theta}\quad;\quad v_g=c'~\sin\theta\]

L’onde glisse donc parallèlement au miroir à une vitesse de phase supérieure à la vitesse de la lumière.

Pour risquer une métaphore : Le front de l’onde ne progresse qu’à la vitesse de groupe, à comparer avec la vitesse de propagation d’une chenille : le front de la chenille progresse moins vite que l’ondulation.

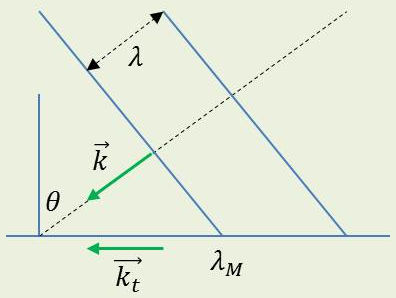C’est ce qu’explique le schéma ci-contre.

Pendant une période, l’onde plane progresse de \(\lambda\) normalement aux plans d’onde, mais le signal électromagnétique progresse de : \[\lambda_M=\frac{\lambda}{\sin\theta}\]

Le signal plan a un vecteur d’onde apparent : \[k_M=\frac{2\pi}{\lambda_M}\qquad\text{à comparer avec :}\quad k=\frac{2\pi}{\lambda}\]

Soit encore : \[k_M=k~\sin\theta=k_t\quad\Rightarrow\quad\overrightarrow{k_M}=\overrightarrow{k_t}\]

Fréquence de coupure du mode \(p\) :

\(k_t\) est réel si : \[\nu~\geq~\nu_p\qquad\text{avec :}\quad\nu_p=\frac{p~c'}{2~a}\]

Si l’on a : \[\nu~>~\frac{c'}{2~a}\]

seul le mode \(0\) peut se propager, avec \(\overrightarrow{E}~\bot~\)[ miroirs ].

3. Propagation entre deux miroirs parallèles

On étudie la propagation d’un champ de pulsation \(\omega\) entre deux miroirs parallèles.

3.1. Préliminaire

Nous allons établir une propriété générale des champs, qu’ils soient électromagnétiques, acoustiques, élastiques... Ces champs sont caractérisés par des fonctions scalaires ou vectorielles obéissant à une équation du type : \[\square\Psi=0\qquad\text{avec :}\quad\square=\Delta-\frac{1}{C'^2}~\frac{\partial^2}{\partial t^2}\]

Nous nous intéressons ici aux champs sinusoïdaux dans le temps : \[\frac{\partial^2}{\partial t^2}~\Psi=-\omega^2~\Psi\]

Nous serons amenés à considérer des termes spatiaux de la forme : \[\exp(j~\overrightarrow{k}\cdot\overrightarrow{q})=\exp\{j~(k_1~q_1+k_2~q_2+k_3~q_3)\}\]

avec : \(k_1,~k_2,~k_3\in\mathbb{C}\) en général.

On note que :

\[\begin{aligned} \Delta\{\exp(j~\overrightarrow{k}\cdot\overrightarrow{q})\}&=-k^2~\exp(j~k~q)\\ \text{avec}~:\qquad k^2&=k_1^2+k_2^2+k_3^2=\frac{\omega^2}{C'^2}\end{aligned}\]

On note aussi que : \[\Delta\Big\{ \begin{pmatrix} \cos \\ \sin \end{pmatrix} k_1~q_1 \begin{pmatrix} \cos \\ \sin \end{pmatrix} k_2~q_2 \begin{pmatrix} \cos \\ \sin \end{pmatrix} k_3~q_3 \Big\}~=~-k^2 \begin{pmatrix} \cos \\ \sin \end{pmatrix} k_1~q_1 \begin{pmatrix} \cos \\ \sin \end{pmatrix} k_2~q_2 \begin{pmatrix} \cos \\ \sin \end{pmatrix} k_3~q_3\]

3.2. Périodicité en y

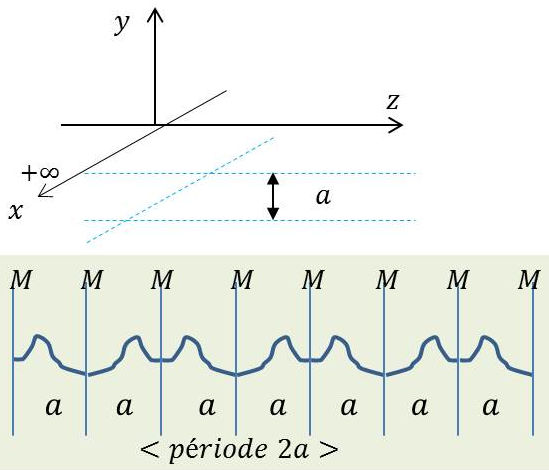Prenons l’image de la fonction \(\Psi\) dans les miroirs de manière à définir cette fonction \(\Psi\) pour toute valeur de \(y\).

On obtient une fonction périodique de période \(2a\), donc décomposable en série de Fourier.

Sur la figure ci-contre, les segments surmontés de la lettre \(M\) sont des miroirs.

On peut toujours supposer que \(\Psi\) est réel, ce qui permet d’obtenir pour l’expression de cette série : \[\Psi=\sum_m \begin{pmatrix} \cos \\ \sin \end{pmatrix} m~k_2~y ~f(x,~z) \begin{pmatrix} \cos \\ \sin \end{pmatrix} \omega~t \quad;\quad k_2=\frac{2\pi}{2~a}\]

On notera par ailleurs que : \[\frac{\partial^2\Psi_p}{\partial y^2}=-m^2~k_2^2~\Psi_p\]

3.3. Variation en x et en z

Du fait de l’inversion de la série de Fourier, chaque terme \(\Psi_p\) de la somme doit satisfaire à : \[\square\Psi_p=0\]

Il vient : \[\frac{\partial^2\Psi}{\partial x^2}+\frac{\partial^2\Psi}{\partial z^2}-\frac{1}{C'^2}~\frac{\partial^2\Psi}{\partial t^2}\]

Cherchons une solution avec propagation selon \(x\) et \(z\) et de pulsation \(\omega\) : \[\Psi_m=A_m~\exp\{j~(\omega~t-k_x~x-k_z~z)\}\]

Nous appellerons image de la fonction \(\Psi\)dans le miroir son extension dans le demi-espace situé derrière le miroir en affectant la même valeur de \(\Psi\) à deux parties symétriques.

Il vient : \[\bar{k}_x^2+\bar{k}_z^2=\bar{k}^2-\bar{k}_y^2=\bar{k}^2-\frac{m^2}{4~a^2}\]

Donc : \({k_x,k_z}~\in~\mathcal{C}\)

Et il y a propagation selon \(k_x,~k_y\) si : \[\bar{k}^2>\frac{m^2}{4~a^2}\qquad\text{ou}\qquad\lambda<\frac{2~a}{m}\qquad\text{ou}\qquad\nu>\frac{m~C'}{2~a}\]

Sinon, il y a atténuation exponentielle selon au moins une direction du plan(\(x,~z\)).

3.3.1. Mode m=0

Toute fréquence peut se propager, mais à \(x,~z,~t\) donnés et \(\Psi\) constant en \(y\).

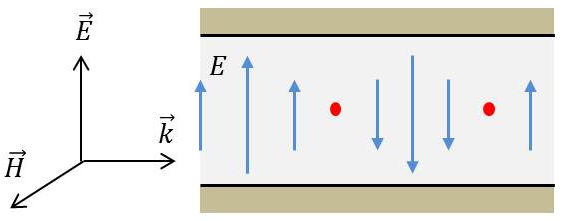Si \(\Psi\) est le champ électrique, les conditions aux limites lui imposent d’être normal au miroir donc : \[E_x=0\qquad\text{et}\qquad E_z=0\]

\(E_y\) est une somme de termes en : \[a_{(k_xk_z)}~\exp\{j~(\omega~t-k_x~x-k_z~z)\}\]

avec : \(k_x^2+k_z^2=k^2\).

Le champ magnétique est parallèle aux miroirs.

Si \({k_x,~k_y}\in\mathbb{R}\), donc de module inférieur à \(k\), le champ qui se propage est une superposition de tranches d’ondes planes polarisées rectiligne, c’est-à-dire : \[\overrightarrow{E}~\bot~\text{(miroirs)}\]

3.3.2. Mode m\(\neq \)0

Le système ne permet la propagation sans atténuation des autres modes qu’à des fréquences supérieures à \(m~C'/2~a\).

\(C'\) : vitesse de phase dans le diélectrique

C’est un filtre passe-haut.

Les fréquences seuil \(m~C'/2~a\) sont les fréquences de coupure des modes \(m\).

4. Propagation entre 4 miroirs

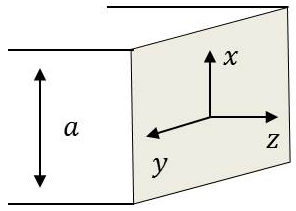Ces quatre miroirs sont supposés parallèles ou orthogonaux deux à deux.

Le champ est de période \(2~a\) en \(x\) et de période \(2~b\) en \(y\), donc \(\Psi\) se présente comme une somme de termes en : \[\begin{pmatrix} \cos \\ \sin \end{pmatrix} l~k_1~x \begin{pmatrix} \cos \\ \sin \end{pmatrix} m~k_2~y~f_m(z,~t) \quad;\quad\bar{k}_1=\frac{1}{2~a}\quad;\quad\bar{k}_2=\frac{1}{2~b}\]

Cherchons pour le mode \(m\) une propagation selon \(z\) : \[f_{lm}(z,~t)=f_{lm}(t-k_z~z)\]

Il vient :

\[\begin{aligned} &k_x^2+k_y^2+k_z^2=k^2=\frac{\omega^2}{C'^2}\\ &\text{soit}~:\quad\bar{k}_z^2=\bar{k}^2-\frac{l^2}{4~a^2}-\frac{m^2}{4~b^2}\end{aligned}\]

Il n’y a de propagation que pour :

\[\begin{aligned} \bar{k}~&>~\sqrt{\frac{l^2}{4~a^2}+\frac{m^2}{4~b^2}}\\ \text{ou}\quad\lambda~&<~\frac{1}{\sqrt{\cfrac{l^2}{4~a^2}+\cfrac{m^2}{4~b^2}}}\\ \text{ou}\quad\nu~&>~C'~\sqrt{\frac{l^2}{4~a^2}+\frac{m^2}{4~b^2}}\end{aligned}\]

La fonction \(\Psi_{lm}\) du mode \(\{lm\}\) étant : \[\Psi_{lm}=a_{lm} \begin{pmatrix} \cos \\ \sin \end{pmatrix} \pi~l~\frac{x}{a} \begin{pmatrix} \cos \\ \sin \end{pmatrix} \pi~m~\frac{y}{b} \begin{pmatrix} \cos \\ \sin \end{pmatrix} (\omega~t-k_z~z)\]

Si \(\Psi\) est le champ électrique \(\overrightarrow{E}\), il faut satisfaire à la condition : \[\overrightarrow{E}~~~\bot~~~\text{[miroirs]}\]

4.1. Discussion

4.1.1. Pas de mode : \(l=m=0\)

\[\overrightarrow{E}=\overrightarrow{E}_{00} \begin{pmatrix} \cos \\sin \end{pmatrix} (\omega~t-k_z~z)\quad;\quad k_z=z\]

Dans la tranche \(z=\text{cte}\), à \(t=t_0\), \(\overrightarrow{E}=\overrightarrow{\text{cte}}\) ne peut être normal aux deux miroirs.

4.1.2. Mode \(H_{10}\)

\[\overrightarrow{E}=\overrightarrow{E}_{10} \begin{pmatrix} \cos \\ \sin \end{pmatrix} \frac{\pi~x}{a} \begin{pmatrix} \cos \\ \sin \end{pmatrix} (\omega~t-k_z~z)\quad;\quad\bar{k}_z^2=\bar{k}^2-\frac{1}{4~a^2}\]

Dans la tranche \(z=\text{cte}\), à \(t=0\), \(\overrightarrow{E}\) est indépendant de \(y\). Or, sur les miroirs verticaux \(E_x=E_z=0\). Pour \(x=a/2\), \(E_y=0\), on a donc : \[E_y=E_{y10}~\cos\frac{\pi~x}{a}~j~(\omega~t-k_z~z)\]

On obtient ensuite \(\overrightarrow{H}\) par : \[\overrightarrow{\text{rot}}\overrightarrow{E}=-\mu~\frac{\partial\overrightarrow{H}}{j~\omega~\mu}\quad;\quad\overrightarrow{H}=-\frac{\overrightarrow{\text{rot}}\overrightarrow{E}}{j~\omega~\mu}\]

\(\overrightarrow{H}\) a une composante selon \(z\), d’où le nom d’onde \(H\).

4.1.3. Modes \(H_{lm}\)

Par définition, \(E_z=0\).

Les seules solutions compatibles avec :

\[\begin{aligned} E_x&=0\quad\text{pour}~~y=\pm \frac{\pi}{2}\\ E_y&=0\quad\text{pour}~~x=\pm \frac{a}{2}\\ {\rm div}~\overrightarrow{E}&=-\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}=0\end{aligned}\]

On a alors, pour \(l,m\) impairs :

\[\begin{aligned} E_x&=E_0~\sin\frac{l~\pi~x}{a}~\cos\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ E_y&=-\frac{l}{m}~\frac{b}{a}~E_0~\cos\frac{l~\pi~x}{a}~\sin\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ E_z&=0\end{aligned}\]

Et on a pour \(l,~m\) pairs :

\[\begin{aligned} E_x&=E_0~\cos\frac{l~\pi~x}{a}~\sin\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ E_y&=-\frac{l}{m}~\frac{b}{a}~E_0~\sin\frac{l~\pi~x}{a}~\cos\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ E_z&=0\end{aligned}\]

Nota : \(H_{00}\) n’existe pas.

Pour \(l\) impair et \(m\) pair (\(H_{10},~H_{12},~H_{30},~H_{32}\dots\)) :

\[\begin{aligned} E_x&=E_0~\sin\frac{l~\pi~x}{a}~\sin\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ E_y&=-\frac{l}{m}~\frac{b}{a}~E_0~\cos\frac{l~\pi~x}{a}~\cos\frac{m\pi y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ E_z&=0\end{aligned}\]

Comme précédemment, on tire \(\overrightarrow{H}\) de la relation : \[\overrightarrow{\text{rot}}\overrightarrow{E}=-\frac{\partial B}{\partial t}=-j~\omega~\mu~H\]

4.1.4. Modes \(E_{lm}\)

Par définition \(H_z=0\).

Les seules solutions compatibles avec :

\[\begin{aligned} H_x&=0\quad\text{pour}~~x=\pm \frac{a}{2}\\ H_y&=0\quad\text{pour}~~y=\pm \frac{b}{2}\\ {\rm div}~\overrightarrow{H}&=-\frac{\partial H_x}{\partial x}+\frac{\partial H_y}{\partial y}=0\end{aligned}\]

sont alors pour \(l,~m\) impairs :

\[\begin{aligned} H_x&=H_0~\cos\frac{l~\pi~x}{a}~\sin\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ H_y&=-\frac{l}{m}~\frac{b}{a}~H_0~\sin\frac{l~\pi~x}{a}~\cos\frac{m~\pi~y}{b}~\exp\{j~(\omega~t-k_z~z)\}\\ H_z&=0\end{aligned}\]

et des expressions analogues pour \(l,m\) pairs ou \(l\) impair et \(m\) pair.

On constaterait à nouveau que \(E_{00}\) n’existe pas.

On tirerait \(\overrightarrow{E}\) de la relation : \[\overrightarrow{\text{rot}}\overrightarrow{E}=\frac{\partial D}{\partial t}=j~\omega~\varepsilon~\overrightarrow{E}\]

On note que les modes \(E_{om}\) vérifient \(H_y=0,~H_z=0\). D’où \(E_y=0,~E_z=0\) ; ce sont des modes \(H_{0m}\).

4.1.5. Modes l, m composites

Une combinaison linéaire des modes \(E_{lm}\) et \(H_{lm}\) pour les mêmes indices \(l\) et \(m\) a pour solution une même combinaison linéaire des solutions précédentes.

On démontre que tout mode \(l,~m\) peut inversement se décomposer en modes \(E_{lm}\) et \(H_{lm}\).