1. Vers une électronique quantique

Les lois de la physique classique s’appliquaient à des composants et des électrons bien localisés dans l’espace. Leur mouvement d’ensemble, même régi par des lois de probabilités, conduisaient à des grandeurs classiques de courant et de tension pour les commandes de fonctions. Toutefois, pour des dimensions de plus en plus petites, la description classique ne peut plus expliquer certains effets nouveaux :

• L’effet d’écluse à électrons : Quand un électron pénètre dans un tels composant, il en élève le niveau d’énergie, empêchant un autre électron d’y pénétrer à son tour.

• Le puits quantique : Comportement ondulatoire en absence de collisions où l’on utilise les effets d’interférences dans les composants eux-mêmes, d’où ce puits quantique.

• La notion de boîte quantique : cavité aux dimensions de quelques dizaines de \(nm\), super atome aux niveaux quasi atomiques où chaque porteur injecté pourrait être récupéré.

Remarque

Avec l’introduction de puits quantiques dans les lasers à semi-conducteurs, on a pu obtenir des vitesses de modulation de quelques dizaines de gigahertz, chaque porteur injecté contribuant directement au gain laser.

Le confinement optique est idéal quand il est possible de canaliser tous les photons générés dans la zone active pour l’émission laser. À cet effet, l’indice de réfraction de la zone active est plus élevé que les matériaux qui l’entourent. Celle-ci devient ainsi le cœur d’un guide optique capable de confiner la lumière émise dans l’axe de la cavité laser.

La taille de ce guide est de l’ordre de la longueur d’onde émise, donc très supérieure aux tailles de quantification électronique évoquées précédemment.

2. Nouvelles technologies et réalités

Dans les nouveaux matériaux (transistors et lasers), les puits quantiques sont obtenus par dépôts de couches de matériaux semi-conducteurs (précision de la distance inter-atomique). Des barrières énergétiques sont ainsi créées pour piéger les électrons et leur imposer un mouvement bidirectionnel. La longueur d’onde et l’énergie sont alors contrôlées.

La rapidité de ces composants et leur faible bruit les rendent très performants (applications aux antennes paraboliques de faible dimension en réception TV par satellite).

Ces composants sont beaucoup plus petits que les fils qui les relient. Il faut alors les considérer dans une architecture particulière, en réseaux organisés en automates communiquant avec des circuits voisins dans des conditions de connexion classique (réseaux neuronaux).

Signalons enfin que, dans les industries de haute technologie comme l’électronique et l’opto-électronique, le microscope à effet tunnel permet un contrôle très précis des surfaces :

En approchant d’une surface (métal ou semi-conducteur), la pointe d’une aiguille métallique, les fonctions d’onde de la pointe et de la surface se recouvrent. Une sorte de tunnel se crée sous la barrière infranchissable que constitue un intervalle libre. Une petite différence de potentiel entre la pointe et la surface suffit (de l’ordre du volt) pour attirer les électrons, d’un côté ou de l’autre. Un courant tunnel prend naissance dans le vide, extrêmement sensible à la distance. Lorsqu’on déplace la pointe le long de la surface, des dénivellations aussi petites que des atomes peuvent faire changer l’intensité de ce courant.

3. Effet laser : dispositifs connexes

Nous rappelons succinctement les principes de deux dispositifs particulièrement intéressants en communications optiques longues distances : l’amplificateur et l’oscillateur.

3.1. Amplificateur optique

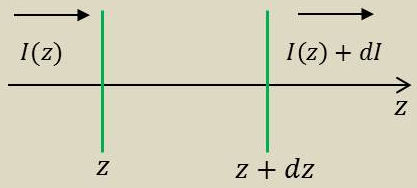Une onde électromagnétique de fréquence \(\nu\) proche des fréquences de transition, se propageant dans un milieu atomique, subit de l’absorption et stimule de l’émission :

• absorption, proportionnelle à \(N_1\) atomes dans l’état (1) contenu dans le volume traversé et qui conduit à une diminution de l’énergie transportée.

• émission stimulée, proportionnelle (même coefficient) à \(N_2\) atomes dans l’état (2) et qui est cohérente avec l’onde incidente et vient donc la remplacer.

On a donc : \[\begin{aligned} dI&=-a~\frac{N_2-N_1}{dz}\\ I(z)&=I_{z=0}~\exp(-\alpha~z)\\ \alpha&=a~(N_2-N_1)\qquad\qquad\text{coeff. d'absorption} \end{aligned} \qquad[1]\]

À l’équilibre thermodynamique, \(N_1\) et \(N_2\) suivent la statistique de Boltzmann : \[\frac{N_1}{N_2}=\exp\Big(\frac{E_2-E_1}{k~T}\Big)=\exp\Big(\frac{h~\nu}{k~T}\Big)\qquad[2]\]

À la température ambiante, \(T_0=300~K\), et aux fréquences optiques \(\nu=6\times 10^{14}\) Hz ou \(\lambda=0,5\times 10^{-3}\) m : \[\frac{N_1}{N_2}=10^{40}\qquad\text{donc~:}\quad N_1\gg N_2\quad\text{et}\quad\alpha>0\qquad[3]\]

Il y a donc diminution de l’intensité.

Pour amplifier, il faut changer le signe de \(\alpha\) par rupture avec la distribution caractéristique à l’équilibre thermique en rendant \(N_2>N_1\). Il se produit une inversion de population.

Avec un dispositif à ondes électromagnétiques, ce sera un effet Maser (Microwave Amplifier by Simulated Emission of Radiation).

Avec un dispositif optique, ce sera un effet Laser (Light Amplifier by Simulated Emission of Radiation), opération qui porte le nom de pompage optique.

3.2. Oscillateur optique

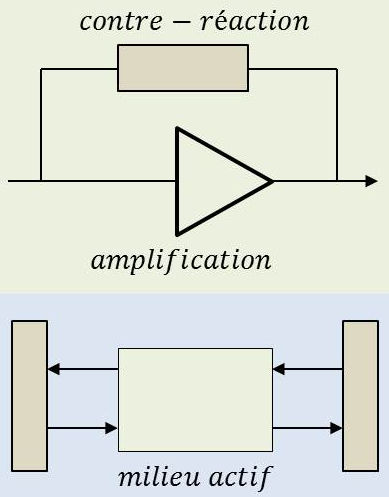Le phénomène de l’oscillateur optique est analogue à l’onde progressive se réfléchissant successivement sur deux miroirs avec amplification à chaque traversée du milieu actif.

Quand l’un des miroirs a un coefficient de réflexion (\(R<1\)), le coefficient de transmission partielle (\(T=1-R\)) permet à l’énergie électromagnétique émise de sortir de la cavité et être utilisée.

La fréquence d’oscillation est donnée par : \[\nu_q=q~\frac{c}{2~L~n}\qquad[4]\]

(voir cavité résonante de Fabry-Perot)

• \(L\) : longueur de la cavité

• \(q\) : nombre de ventres (ou de noeuds du système)

Soit \(G\) le gain apporté par la propagation dans le milieu actif par unité de longueur. Le nombre de photons dans la cavité est donné par : \[P=\frac{E}{h~\nu}\qquad[5]\]

La puissance optique est alors définie par : \[P_0=h~\nu~\Big\{-\frac{\ln(R)}{2~\ln(G)/c}\Big\}~P\qquad[6]\]

4. Sources bibliographiques

• Rapport de conjoncture 1993
  CNRS

• Les communications optiques
  Conseil scientifique France Telecom (Mémento technique, n° 3, 1994)

• Quand l’électronique devient quantique
  C. Weisbuch (État des sciences et des techniques, Éd. La découverte, FPH, 1991)

• Des microscopes pour voir les atomes
  E. Giacobino (État des sciences et des techniques, Éd. La découverte, FPH, 1991)

• Les frontières physiques de la micro-électronique
  R. Rosencher, D. Bois (La Recherche, n° 203, octobre 1988)

• Des écluses à électrons
  M. Maashal (La Recherche, n° 227, décembre 1990)

• Les lasers à semi-conducteur
  C. Weisbuch, B. de Crémoux (La Recherche, 1991)

• L’avènement de la nano-électronique
  C. Weisbuch (La Recherche, novembre 1991)

• Le microscope à effet tunnel
  F. Salvan (La recherche, n° 181, octobre 1986)