1. Multiplication temporelle

La multiplication temporelle est la multiplication au sens classique du terme de deux fonctions : \[z(t)=x(t)~y(t)\]

1.1. Action de l’impulsion de Dirac

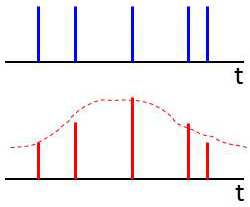La figure 1 représente un train d’impulsions de Dirac. On peut l’exprimer mathématiquement par : \[u(t)=\sum_i\delta(t-t_i)\]

La figure 2 comprend deux représentations conjointes :

• un signal \(x(t)\) en représentation continue (en pointillés) ;

• un signal résultant de la multiplication de \(x(t)\) par \(u(t)\), pondération ou effet de masque.

On exprimera ce signal par : \[y(t)=u(t)~x(t)=\sum_ix(t_i)~\delta(t-t_i)\] Il s’agit des valeurs de \(x(t)\), prélevées aux instants \(t_i\) de présence des impulsions.

1.2. Action de l’échelon de Heaviside

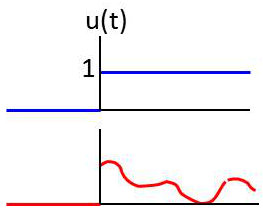La figure 1 représente la fonction échelon \(u(t)\) :

\[\left\lbrace \begin{aligned} u(t)&=1 &&\qquad t\geq 0\\ u(t)&=0 &&\qquad t<0 \end{aligned} \right.\]

La figure 2 représente la fonction : \[y(t)=u(t)~x(t)\]

On a donc :

\[\left\lbrace \begin{aligned} y(t)&= x(t) &&\quad t\geq 0\\ y(t)&= 0 &&\quad t<0 \end{aligned} \right.\]

1.3. Action de la fonction porte

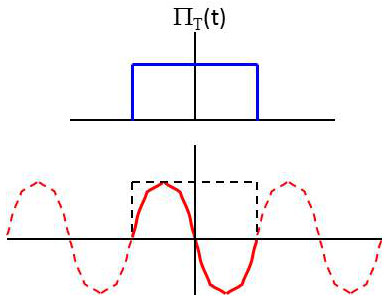La fonction porte d’ouverture \(T\) a pour expression :

\[\left\lbrace \begin{aligned} \Pi_T(t)&= 1 &&\quad t \in [-T/2~;~+T/2]\\ \Pi_T(t)&= 0 &&\quad t \notin [-T/2~;~+T/2] \end{aligned} \right.\]

Après l’action de la porte (masque), on obtient un signal : \[y(t)=x(t)~\Pi_T(t)\]

La figure représente un cas très particulier et fréquemment utilisé, celui d’une sinusoïde tronquée sur une période, l’ouverture \(T\) de la porte correspondant à cette période \(T\)

1.4. Modulation d’amplitude (battement)

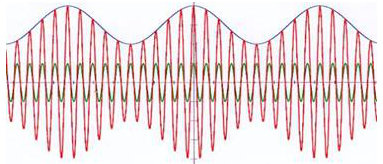La figure ci-contre représente une modulation d’amplitude avec porteuse. Elle résulte de la multiplication des deux signaux entre eux :

\[\left\lbrace \begin{aligned} \ s_0(t)&=a_0~\cos(\omega_0~t)\\ \ s_1(t)&=k+a_1~\cos(\omega_1~t)\\ \ s(t)&=s_0(t)~s_1(t) \end{aligned} \right.\]

On dit que la sinusoïde haute fréquence porte la sinusoïde basse fréquence ou encore que la sinusoïde basse fréquence module la sinusoïde haute fréquence.

2. Convolution des signaux

Le produit de convolution (noté \(\star\)) est fondamental, car il associe tout signal à une fonction impulsion de Dirac \(\delta(t)\), élément neutre de l’opération : \[x(t)\star\delta(t)=\int_{-\infty}^{+\infty}x(\tau)~\delta(t-\tau)~d\tau=x(t)\]

Une autre formule remarquable s’en déduit : \[x(t)\star\delta(t-t_0)=x(t-t_0)\]

La convolution d’un signal \(x(t)\) par une impulsion de Dirac centrée sur \(t_0\) revient donc à translater ce signal de \(t_0\).

Physiquement, la convolution (qui introduit une partie retard temporel) correspond à un filtrage de ce signal à son passage dans un système de transmission.

3. Signaux périodiques. Séries de Fourier

Tout signal périodique \(x(t)\) de période \(T\) peut s’écrire sous la forme d’une série :

\[\left\lbrace \begin{aligned} x(t)&=\sum_{-\infty}^{+\infty}C_n~exp\Big(j~2\pi~\frac{n}{T}~t\Big)\\ C_n&=\frac{1}{T}\sum_{-T/2}^{+T/2}x(t)~exp\Big(j~2\pi~\frac{n}{T}~t\Big)dt \end{aligned} \right.\]

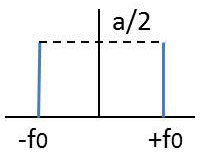
On sait que le spectre en amplitude d’une fonction sinusoïdale se compose de deux raies symétriques :

\[\left\lbrace \begin{aligned} s(t)&=a~\cos(2\pi~f_0~t)\\ S(f)&=\frac{a}{2}~\{\delta(f-f_0)+\delta(f+f_0)\} \end{aligned} \right.\]

On trouvera facilement pour le spectre en amplitude de \(x(t)\) : \[X(f)=\sum_{-\infty}^{+\infty}C_n~\delta\Big(f-\frac{n}{T}\Big)\]

Il s’agit d’un spectre de raies d’amplitude \(C_n\) régulièrement espacées de \(1/T\).

4. Signaux apériodiques. Transformation de Fourier

Si le signal \(x(t)\) n’est pas périodique, on peut toujours supposer qu’il l’est en admettant que la période \(T\) devient infinie. Dans ces conditions, \(1/T\) tend vers zéro, l’espacement entre les raies diminue et le spectre devient un spectre continu.

Donc, si \(x(t)\) n’est pas périodique, on passe de sa représentation temporelle \(x(t)\) à sa représentation fréquentielle (spectre) \(X(f)\) au moyen de la transformation de Fourier. Cette transformation s’adapte à n’importe quel signal apériodique.

On rappelle les formules de transformation directe et inverse :

\[\left\lbrace \begin{aligned} x(t)\quad\rightarrow\quad X(f)&=\int_{-\infty}^{+\infty}x(t)~exp(-j~2\pi~f~t)~dt\\ X(f)\quad\rightarrow\quad~~x(t)&=\int_{-\infty}^{+\infty}X(f)~exp(+j~2\pi~f~t)~df \end{aligned} \right.\]

Une intégrale est d’ailleurs très utile à connaître en transformation de Fourier \((x\in R)\) : \[\int_{-\infty}^{+\infty}\exp(-a~x^2\pm2~b~x-c)~dx=\sqrt{\frac{\pi}{a}}~\exp(-\frac{a~c-b^2}{a}) \quad;\quad a,~b,~c\in (\mathbb R~\rm ou~\mathbb C)\]

Un exemple bien connu, pour \(a=1,\ b=c=0\) : \[\int_0^{+\infty}e^{-x^2}~dx=\frac{1}{2}\int_{-\infty}^{+\infty}e^{-x^2}~dx=\frac{\sqrt{\pi}}{2}\]

Remarque

D’une manière générale \(X(f)\) est une quantité complexe que l’on peut mettre sous la forme : \[X(f)=|X(f)|~e^{j~\phi(f)} \quad~;~\quad \varphi(f)={\rm Arg}\big[X(f)\big]\]

Si \(x(t)\) est un signal réel, \(X(f)\) possède la propriété de symétrie hermitienne, c’est-à-dire : \[X(-f)=\overline{X(f)} \quad;\quad {\rm Arg}\big[X(-f)\big]= {\rm Arg}\big[\overline{X(f})\big]=-{\rm Arg}\big[X(f)\big]\]

En conclusion : Si \(x(t)\) est un signal réel, le module de \(X(f)\) est une fonction paire et la phase de \(X(f)\) est une fonction impaire.

5. Théorèmes de la physique des signaux

5.1. Théorème de Plancherel

L’application du théorème de Plancherel est importante dans la transmission des signaux (systèmes en cascade). Il s’énonce ainsi :

On considère trois signaux \(x(t)\), \(y(t)\) et \(z(t)\) dont les spectres en fréquence sont respectivement \(X(f)\), \(Y(f)\) et \(Z(f)\) : \[z(t)=x(t)~y(t) \quad \Rightarrow \quad\ Z(f)=X(f)\star Y(f)\]

Et réciproquement : \[z(t)=x(t)\star y(t) \quad \Rightarrow \quad Z(f)=X(f)~Y(f)\]

Ainsi, l’opération de convolution dans un espace devient un produit dans l’autre espace.

5.2. Théorème de Parseval

L’application du théorème de Parseval est fondamentale dans les problèmes de puissance et d’énergie de signaux. Il s’énonce ainsi :

On considère deux signaux \(x(t)\) et \(y(t)\) de spectres respectifs \(X(f)\) et \(Y(f)\). On peut écrire : \[\int_{-\infty}^{+\infty}x(t)~\overline{y(t)}~dt=\int_{-\infty}^{+\infty}X(f)~\overline{Y(f)}~df\]

En particulier : \[\int_{-\infty}^{+\infty}|x(t)|^2~dt=\int_{-\infty}^{+\infty}|X(f)|^2~df\]

Ainsi, les calculs énergétiques peuvent être menés dans l’espace des temps ou dans l’espace des fréquences selon la complexité des expressions dans un espace ou dans l’autre.

6. Transformées de Fourier utiles

\[\begin{aligned} \text{Espace des temps} \qquad &\Leftrightarrow \qquad \text{Espace des fréquences}\\ x(t-a) \qquad &\Leftrightarrow \qquad e^{-j~2\pi~f~a}~X(f)\\ x(t)~e^{j~2\pi~f_0~t} \qquad &\Leftrightarrow \qquad X(f-f_0)\\ \\ \delta(t) \qquad &\Leftrightarrow \qquad 1\\ 1 \qquad &\Leftrightarrow \qquad \delta(f)\\ \\ e^{j~2\pi~f_0~t} \qquad &\Leftrightarrow \qquad \delta(f-f_0)\\ \delta(t-t_0) \qquad &\Leftrightarrow \qquad e^{-j~2\pi~f~t_0}\\ \\ \cos(2\pi~f_0~t) \qquad &\Leftrightarrow \qquad \frac{1}{2}~\{\delta(f+f_0)+\delta(f-f_0)\} \\ \sin(2\pi~f_0~t) \qquad &\Leftrightarrow \qquad \frac{1}{2}~\{\delta(f+f_0)-\delta(f-f_0)\} \\ \\ x(t)~\cos(2\pi~f_0~t) \qquad &\Leftrightarrow \qquad \frac{1}{2}~\{X(f+f_0)+X(f-f_0)\}\\ \\ x(t)\star y(t) \qquad &\Leftrightarrow \qquad X(f)~~Y(f)\\ x(t)\star\overline{y(-t)} \qquad &\Leftrightarrow \qquad X(f)~~\overline{Y(f)}\\ \\ \frac{d^n}{dt^n}x(t) \qquad &\Leftrightarrow \qquad (j~2\pi~f)^n~X(f)\\ (-j~2\pi~t)^n\ x(t) \qquad &\Leftrightarrow \qquad \frac{d^n}{df^n}X(f) \end{aligned}\]