1. Généralités

La variable aléatoire permet de modéliser un certain nombre de phénomènes physiques dont le signal. Cependant, il y a le phénomène aléatoire en tant que tel (par exemple une amplitude, un angle, etc.), mais accompagné du paramètre temps. L’art consistera à associer les deux.

On appellera signal aléatoire un signal \(X(t,~\omega)\). On peut le considérer sous deux points de vue :

1) Le point de vue temporel : on étudie les fonctions déterministes \(X(t_0,~\omega)\) pour différentes valeurs fixées de \(\omega_0\). C’est une fonction ordinaire du temps avec une signification physique : le résultat d’une mesure du phénomène aléatoire étudié.

2) Le point de vue statistique : on étudie les propriétés de \(X(t_0,~\omega)\) pour différentes valeurs fixées de \(t_0\). Elle n’a pas de signification physique : il n’est en effet pas concevable, à tout instant fixé, d’avoir accès à la mesure de \(X(t_0,~\omega),~\forall\omega\). Ceci supposerait une infinité d’expériences identiques, indépendantes et simultanées.

1.1. Exemple type

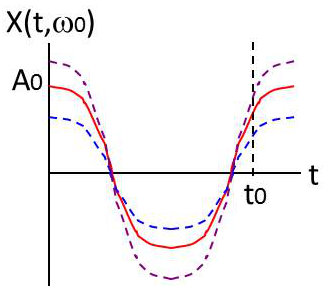Prenons le cas de la sinusoïde : \[X(t,~\omega)=A~\cos(\omega_0~t)\]

\(A\) est une variable aléatoire continue et uniformément répartie dans l’intervalle \(A\in[A_0-a,~A_0+a]\).

La courbe représentée en rouge est la courbe nominale (pour la valeur théorique de l’amplitude). Les deux autres courbes sont obtenues avec une variation d’amplitude.

On notera que, quelle que soit la représentation, la forme de la courbe (donc du phénomène) est inchangée avec conservation stricte de la période. On remarquera par exemple que pour une valeur fixée de \(t_0\), on a obtenu trois valeurs possibles de l’amplitude (trois expériences).

2. Moments temporels

\(X(t,~\omega)\) étant un processus aléatoire réel ou complexe, on sait que \(X(t,~\omega_0)\) est une fonction déterministe du temps (pour cette valeur de \(\omega_0\) représentant une observation particulière d’un phénomène physique aléatoire.

On définit un moment d’ordre 1 ou moyenne temporelle : \[\langle X(t,~\omega_0)\rangle =lim_{T\rightarrow 0}\left[\frac{1}{T}\int_{-T/2}^{+T/2}X(t,~\omega_0)~dt\right]\]

On définit le moment d’ordre 2 ou fonction d’auto-corrélation temporelle par :

\[\begin{aligned} R_{xx}(\tau,~\omega_0)&=\langle X(t,~\omega_0)~X(t-\tau,~\omega_0)~\rangle \\ R_{xx}(\tau,~\omega_0)&=lim_{T\rightarrow 0}\left[\frac{1}{T}\int_{-T/2}^{+T/2}X(t,~\omega_0)~X(t-\tau,~\omega_0)~dt\right] \quad;\quad X(t,~\omega_0)\in \mathbb{R}\end{aligned}\]

Dans le cas d’un processus complexe : \[R_{xx}(\tau,~\omega_0)=\langle X(t,~\omega_0)~\overline{X(t-\tau,~\omega_0)}~\rangle\]

Ces grandeurs sont fonction de l’échantillon choisi.

3. Moments statistiques

Pour un instant \(t_0\) fixé, le processus aléatoire \(X(t,~\omega)\) devient une variable aléatoire \(X(t_0,~\omega)\) dont on sait calculer :

• la moyenne statistique \(E[X(t,~\omega_0)]\) ;

• la fonction d’autocorrélation statistique \(R_{xx}(t_1,~t_2,~\omega)\).

\[\begin{aligned} R_{xx}(t_1,~t_2,\omega)&=E\big[X(t_1,\omega)~X(t_2,~\omega)\big] &&X(t,~\omega)\in \mathbb{C} \\ R_{xx}(t_1,~t_2,\omega)&=E\big[X(t_1,\omega)~\overline{X(t_2,~\omega)}\big] &&X(t,~\omega)\in \mathbb{C}\end{aligned}\]

4. Stationnarité au sens large (ordre 2)

Dorénavant, on notera le processus aléatoire \(X(t,~\omega)\) en abrégé \(X(t)\).

Un signal aléatoire est dit stationnaire au sens large si sa moyenne statistique est indépendante du temps et si sa fonction d’auto-corrélation n’est fonction que de l’écart temporel : \[E[X(t)]=cte \quad;\quad R_{xx}(t_1,~t_2)=R_{xx}(t_1-t_2)\]

5. Ergodisme

Un processus aléatoire est dit ergodique lorsque les moyennes temporelles de tous les échantillons existent et sont indépendantes de l’échantillon.

La seule classe de processus aléatoires que nous retiendrons pour la pratique en théorie du signal est celle des processus à la fois stationnaires et ergodiques. Un théorème fondamental concerne ces signaux :

Théorème de Birkhoff

Si un processus est à la fois stationnaire et ergodique, alors les moments temporels et les moments statistiques sont égaux.

Ce théorème est fondamental : il montre que les propriétés statistiques des processus stationnaires et ergodiques peuvent être obtenus par l’observation d’une seule réalisation.

L’observation particulière, pendant un temps suffisamment long, permet, avec une précision convenable, de connaître les propriétés statistiques de l’ensemble des réalisations possibles. Ce résultat est heureux, car l’observation de l’ensemble des réalisations possibles du processus, à un instant donné, est elle-même physiquement impossible.

6. Analyse spectrale du processus

Il est mathématiquement délicat de définir l’analogue de la transformée de Fourier pour un signal aléatoire. On raisonne plutôt sur les moments statistiques du signal aléatoire, supposé stationnaire au sens large.

La représentation spectrale dans le domaine des fréquences remplace le signal aléatoire stationnaire \(X(t)\) par le signal déterministe \(R_{xx}(t)\). Elle mesure la répartition de puissance dans le domaine des fréquences.

Soit \(x(t)\) un signal aléatoire réel ou complexe stationnaire au second ordre. Sa fonction d’auto-corrélation s’écrit : \[R_{xx}(\omega)=E\big[x(t)~\overline{x(t-\tau)}\big]\]

Le théorème de Wiener-Khintchine permet d’assurer, sous certaines conditions, que la densité spectrale de puissance \(S_{xx}(f)\) d’un signal aléatoire de fonction d’autocorrélation \(R_{xx}(t)\) est égale à : \[S_{xx}(f)={\rm TF}\big[R_{xx}(\tau)\big]\]

On aura alors : \[P=R_{xx}(0)=\int_{-\infty}^{+\infty}S_{xx}(f)~df\]

7. Notion de bruit blanc

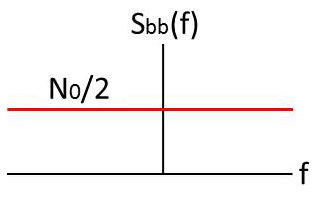Un bruit blanc est un signal aléatoire \(b(t)\) stationnaire au second ordre dont la densité spectrale de puissance est constante sur tout l’axe des fréquences :

\[\begin{aligned} S_{bb}(f)&=\frac{N_0}{2} \qquad \forall f \\ R_{bb}(\tau)&=\frac{N_0}{2}~\delta(\tau)\end{aligned}\]

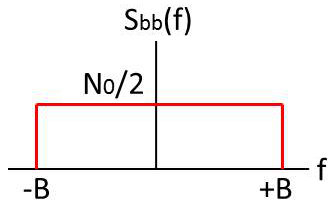Comme le montre la figure, le bruit est de puissance moyenne infinie, ce qui correspond à une idéalisation de la réalité.

Schématiquement, on assimilera à un bruit blanc tout signal dont la densité spectrale est constante dans une bande beaucoup plus large que la bande dans laquelle on l’observe. On peut donc définir un bruit blanc à bande limitée (bruit pseudo-blanc) par :

\[\begin{aligned} S_{bb}(f)&=\frac{N_0}{2} \qquad |f|<B\\ S_{bb}(f)&=0 \quad\qquad \text{ailleurs}\end{aligned}\]

D’où l’on déduit : \[R_{bb}(\tau)=N_0~B~\sin c~(2\pi~B~\tau)\]

La formule montre qu’un tel bruit converge vers un bruit blanc lorsque \(B\) tend vers l’infini, car le sinus cardinal reste une quantité finie.

Tout bruit sera considéré comme un processus aléatoire stationnaire d’ordre 2, centré, additif et indépendant du signal aléatoire auquel il vient se superposer.

On a vu que le bruit blanc n’existait pas réellement. Mais on s’en approche avec le bruit émis par le rayonnement du corps noir régi par la loi de Planck. La DSP d’un tel bruit est exprimée par la formule : \[S_{bb}(f)=\frac{h~f}{e^{h~f/k~T}-1}\]

• h : constante de Boltzmann

• k : constante de Planck

• T : température absolue (en kelvins) du corps noir

On remarque que, si \(hf \ll kT\) (cas des fréquences radioélectriques), on a : \[e^{h~f/k~T}\thickapprox 1+\frac{h~f}{k~T}\]

Il s’ensuit que : \[S_{bb}(f)=k~T=cte\]

On fait souvent l’hypothèse supplémentaire que le bruit blanc est gaussien, ce qui est le cas du bruit thermique produit par une résistance.

Ces deux hypothèses sont toutefois indépendantes, le terme bruit blanc faisant appel aux propriétés énergétiques du processus alors que le terme gaussien fait appel à des propriétés statistiques.

On dit qu’un signal aléatoire \(X(t\)) -– et en particulier un bruit blanc -– est gaussien si, quelle que soit la suite de N instants \(\{t_i\}\), la variable aléatoire à N dimensions \(\{X(t_i)\}\) est une variable gaussienne, c’est-à-dire dont la densité de probabilité suit une loi de Gauss.

Si \(b(t)\) est un bruit blanc centré gaussien :

\[\begin{aligned} f(b)&=\frac{1}{\sigma\sqrt{2\pi} }e^{-b^2/2~\sigma^2}\\ P_b&=R_{bb}(0)=E\big[b(t)~b(t)\big]=E\big[b^2(t)\big]\\ P_b&=\int_{-\infty}^{+\infty}\frac{1}{\sigma~\sqrt{2\pi}}~e^{-b^2/2~\sigma^2}~db\end{aligned}\]

Posant \(u=\cfrac{b}{\sigma~\sqrt{2}}\) , il vient :

\[\begin{aligned} P_b&=\frac{2~\sigma^2}{\sqrt{\pi}}\int_{-\infty}^{+\infty}u^2~e^{-u^2}~du \\ P_b&=\frac{2~\sigma^2}{\sqrt{\pi}}~\frac{\sqrt{\pi}}{2}=\sigma^2\end{aligned}\]

D’où une importante remarque : si \(b(t)\) est un bruit blanc gaussien centré, la variance \(\sigma^2\) est égale à la puissance moyenne de bruit. Un bruit blanc à bande limitée aura comme puissance de bruit : \[P=\int_{-\infty}^{+\infty}S_{bb}(f)=\frac{N_0}{2}~2~B=N_0~B\]

8. Exemple de processus aléatoire classique

On s’intéresse au signal sinusoïdal à phase aléatoire \(\Phi\) répartie uniformément sur \([0,~2\pi]\).

Étudions la stationnarité et l’ergodisme de x(t). Le caractère aléatoire de \(x(t)\) est uniquement dû à la variable aléatoire dont la densité de probabilité est :

\[\begin{aligned} &&&f(\Phi)=\frac{1}{2\pi} &&\Phi\in[0,~2\pi]\\ &&&f(\Phi)= 0 &&\text{ailleurs}\end{aligned}\]

8.1. Stationnarité à l’ordre 1

\[E\{X(t)\}=E\{A\cos(2\pi f_0t+\Phi)\}\]

D’après le théorème de la moyenne : \[E\{X(t)\}=\frac{A}{2\pi}\int_0^{2\pi}\cos(2\pi f_0t+\Phi)~d\Phi=0\]

Ce résultat étant indépendant de \(t\), la stationnarité à l’ordre 1 est donc vérifiée.

8.2. Stationnarité à l’ordre 2

\[\begin{aligned} R_{xx}(t,~\tau)&=E\{x(t)~\overline{x(t-\tau}\}\\ R_{xx}(t,~\tau)&=\frac{A^2}{2\pi}\int_0^{2\pi}\cos(2\pi~f_0~t+\Phi)~\cos\big[2\pi~f_0~(t-\tau)+\Phi\big]~d\Phi\\ R_{xx}(t,~\tau)&=\frac{A^2}{4\pi}\int_0^{2\pi}~\big\{\cos\big[2\pi~f_0~(2~t-\tau)+2~\Phi)\big]+\cos(2\pi~f_0~\tau)\big\}~d\Phi\\ R_{xx}(t,~\tau)&=\frac{A^2}{4\pi}~\cos(2\pi~f_0~\tau)\int_0^{2\pi}d\Phi=\frac{A^2}{2}~\cos(2\pi~f_0~\tau)\end{aligned}\]

Ce résultat étant indépendant de \(\tau\), la stationnarité au sens large est donc vérifiée.

8.3. Ergodisme à l’ordre 1

\[\begin{aligned} \langle x(t,\Phi)\rangle&=lim_{T\rightarrow \infty}\left\{\frac{A}{T}\int_{-T/2}^{+T/2}\cos(2\pi~f_0~t+\Phi)~dt\right\}\\ \langle x(t,\Phi)\rangle&=lim_{T\rightarrow \infty}\left\{\frac{A}{T}~\frac{\sin(2\pi~f_0~t+\Phi)}{2\pi~f_0}\right\}_{-T/2}^{+T/2}\\ \langle x(t,\Phi)\rangle&=lim_{T\rightarrow \infty}\left\{\frac{A}{T}~\frac{\sin(\pi~f_0~T+\Phi)+\sin(\pi~f_0~T-\Phi)}{2\pi ~f_0}\right\}=0\end{aligned}\]

Ce résultat étant indépendant de \(\Phi\), le processus est ergodique à l’ordre 1.

8.4. Ergodisme à l’ordre 2

\[\begin{aligned} &\langle x(t,~\Phi)~x(t-\tau,~\Phi)\rangle \\ &\qquad=lim_{T\rightarrow \infty}\left\{\frac{A}{T}\int_{-T/2}^{+T/2}\cos(2\pi~f_0~t+\Phi)~\cos\big[2\pi~f_0~(t-\tau)+\Phi\big]~dt\right\}\\ &\qquad=lim_{T\rightarrow \infty}\left\{\frac{A}{T}\int_{-T/2}^{+T/2}\cos\big[2\pi~f_0~(2~t-\tau)+2~\Phi\big]~dt +\int_{-T/2}^{+T/2}\cos(2\pi~f_0~\tau)~dt\right\}\\ &\qquad=\frac{A^2}{2}~\cos(2\pi~f_0~\tau)\end{aligned}\]

Ce résultat étant indépendant de \(\Phi\), le processus est donc ergodique au sens large.

Remarque

Le signal sinusoïdal à phase aléatoire et uniformément répartie sur \([0,~2\pi]\) fournit un excellent exemple de processus à la fois stationnaire et ergodique. Par ailleurs, les moments statistiques et temporels d’un même ordre sont égaux, ce qui permet de faire référence au théorème de Birkhoff :

Dans une application ergodique, moyenne spatiale et moyenne temporelle sont égales presque partout.