1. Filtrage linéaire et invariant dans le temps

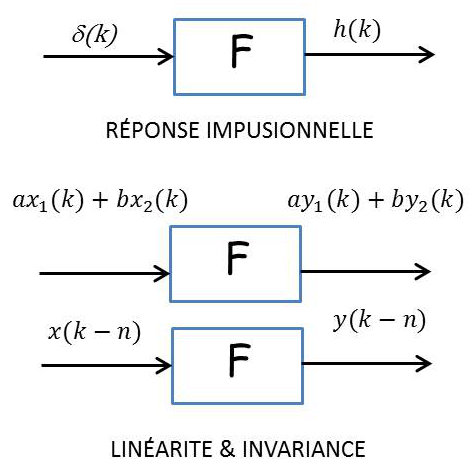On retrouve les mêmes définitions que pour les signaux continus et exprimés par les schémas ci-contre.

Comme on a :

\[\begin{aligned} y(k)&=F\{x(t)\}=F\big\{\sum_{n=-\infty}^{+\infty}x(n)~\delta(k-n)\big\}\\ y(k)&=\sum_{n=-\infty}^{+\infty}F\big[x(n)~\delta(k-n)\big]\\ y(k)&=\sum_{n=-\infty}^{+\infty}x(n)~h(k-n) \\ y(k)&=x(k)\star h(k) \quad \Rightarrow \quad Y(z)=X(z)~H(z)\end{aligned}\]

\(H(z)\) transformation en \(z\) de \(h(t)\) est par définition la fonction de transfert en \(z\) du filtre.

Par exemple, l’opération de retard \(y(k)=x(k-n)\) correspond à un filtrage linéaire et invariant dans le temps (FLIT) de réponse impulsionnelle \(h(k)=\delta(k-n)\) et donc de fonction de transfert \(H(z)=z^{-n}\).

2. Équations de récurrence

Aux équations différentielles linéaires, à coefficients constants, des FLIT à temps continu correspondent les équations de récurrence linéaire, également à coefficients constants, pour les FLIT à temps discret. Nous nous limitons ici aux filtres dont la relation entrée – sortie est régie par ce type d’équation.

La sortie \(y(k)\) est alors reliée à l’entrée \(x(k)\) par une relation de la forme : \[\sum_{n=0}^N a_n~y(k-n)=\sum_{j=0}^P b_j~x(k-j) \qquad a_0\neq 0\]

D’où : \[y(k)=\frac{1}{a_0}\left\{\sum_{j=0}^Pb_j~x(k-j)-\sum_{n=1}^N a_n~y(k-n)\right\}\]

3. Fonctions de transfert

En appliquant la transformation en \(Z\) à la première relation, il vient : \[\sum_{n=0}^N a_n~z^{-n}~Y(z)=\sum_{j=0}^P b_j~z^{-j}~X(z)\]

D’où la fonction de transfert (en \(z\)) : \[H(z)=\frac{Y(z)}{X(z)}=\frac{\sum_{j=0}^P b_j~z^{-j}}{\sum_{n=0}^N a_n~z^{-n}}\]

Remarque

Connaissant la fonction de transfert en \(z\), on obtient la fonction de transfert correspondante dans le plan des fréquences (fonction de transfert en \(f\)) en posant \(z=exp(j~2\pi f)\).

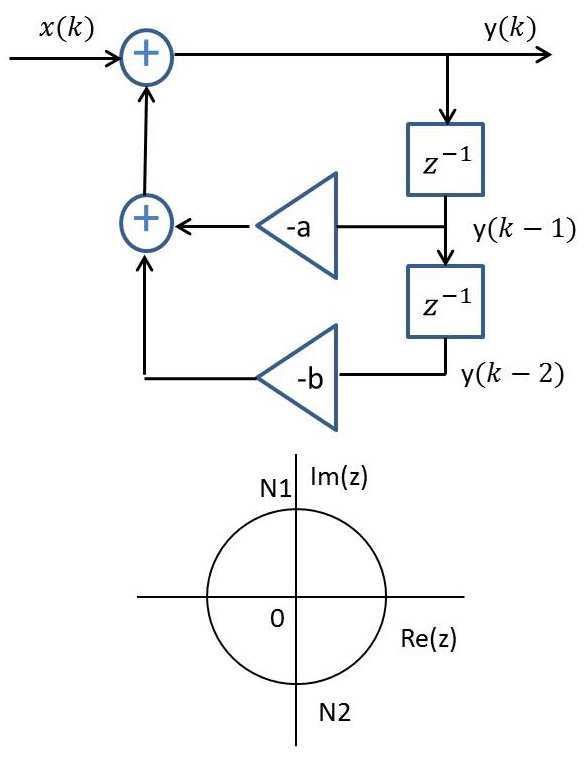
4. Conditions de réalisation

À une expression donnée \(H(z)\) correspondent en général plusieurs réponses \(h(k)\) en fonction du domaine de convergence choisi. Une seule sera causale.

À la fonction : \[H(z)=\frac{\sum_{j=0}^P b_j~z^{-j}}{\sum_{n=0}^N a_n~z^{-n}}=\frac{b_0\prod_{j=0}^P(1-N_j~z^{-1})}{a_0\prod_{n=0}^N(1-P_n~z^{-1})}\]

ne doit correspondre qu’une seule réponse impulsionnelle \(h(k)\) causale associée au domaine de définition \(|z|>sup|P_i|\), à condition que le degré du numérateur de \(H(z)\) soit inférieur ou égal au degré du dénominateur.

Remarque

Pour que le filtre soir réalisable, il faut que les coefficients soient réels, donc que les zéros \(N_j\) et les pôles \(P_n\) soient réels ou complexes conjugués.

Comme pour les filtres à temps continu, un filtre sera stable si sa réponse à tout signal borné est bornée. Une condition équivalente sera ici : \[\sum_{k=-\infty}^{k=+\infty}|H(k)|<+\infty\]

Cette condition est elle-même équivalente au fait que la série \( \sum_{k=-\infty}^{k=+\infty}H(k)~z^{-k} \) est absolument convergente sur le cercle unité, donc que le cercle unité appartienne au domaine de convergence de \(H(z)\). Ce qui signifie que tous les pôles du filtre sont strictement à l’intérieur de ce cercle unité.

En résumé : Un filtre est causal et stable si et seulement si le degré du numérateur de \(H(z)\) en tant que fraction rationnelle en \(z\) est inférieur ou égal au degré du dénominateur et tous les pôles du filtre sont strictement à l’intérieur du cercle unité.

5. Applications

L’étude de la réalisation physique n’a pas tout à fait sa place ici, car elle relève du traitement de signal. Nous avons cependant choisi un exemple très simple, celui du filtre transversal, de façon à illustrer ce qui vient d’être dit.

Un filtre transversal est un filtre pour lequel \(H(z)\) est un polynôme en \(z~(N = 0)\). Nous conviendrons en outre pour simplifier l’écriture que \(a_0=1\).

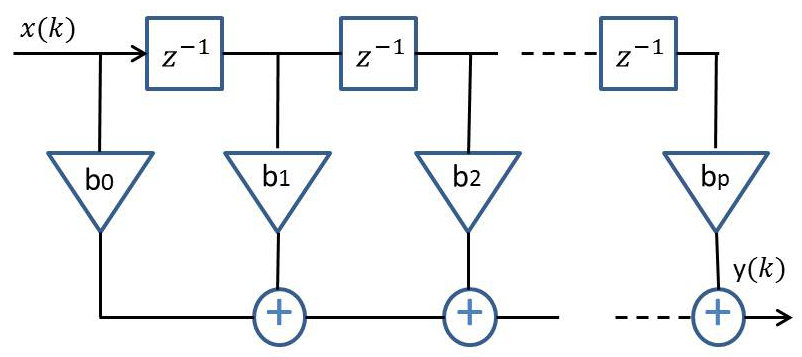Le schéma-bloc ci-contre réalise la relation entrée – sortie, \(P\) étant l’ordre du filtre d’ordre (\(P\) éléments de retard) :

\[\left\{ \begin{aligned} y(k)&=\sum_{j=0}^{P}b_j~x(k-j) \\ H(z)&=\sum_{j=0}^Pb_j~z^{-j} \end{aligned} \right.\]

La réponse impulsionnelle est \(h(k)\) telle que :

\[h(k)=\left\{ \begin{aligned} b_k &\qquad 0\leq k\leq P\\ 0 &\qquad \text{ailleurs} \end{aligned} \right.\]

Exemple d’un filtre sélectif :
– Fréquence de résonance normalisée : \(f_0=0.25\)
– Position des deux pôles : \(P_1=+0.9~i\) et \(P_2=-0.9~i\)

Expression de la fonction de transfert en \(z\) :

\[\begin{aligned} H(z)&=\frac{1}{(1-0.9~z^{-1})(1+0.9~z^{-1})}\\ H(z)&=\frac{1}{1-0.81~z^{-2}} = \frac{1}{1-0.81~e^{-j4\pi f}}\end{aligned}\]

La deuxième expression de \(H(z)\) permet d’écrire la relation de récurrence : \[y(k)=x(k)-0.81~y~(k-2)\]

Pour le calcul de la réponse impulsionnelle, nous partons de l’expression de la fonction de transfert en \(z\) dont nous modifions l’écriture pour éviter le recours à la transformée inverse. \[H(z)=\frac{1}{1-0.81~z^{-2}}=\sum_{k=o} ^{+\infty}(0.81~z^{-2})^k=\sum_{k=o} ^{+\infty}(0.81)^kz^{-2k}=\sum_{k=-\infty}^{+\infty}h(k)~z^{-k}\]

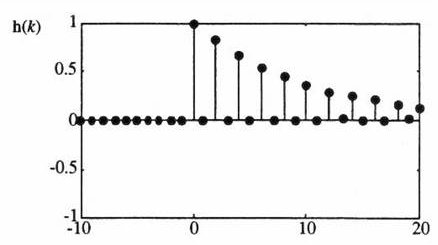Ainsi, nous avons :

\[h(k)=\left\{ \begin{aligned} &(0.81)^p &&\qquad k=2p &&\quad p\geq 0 \\ &0 &&\qquad k=2p+1 &&\quad p\geq 0 \\ &0 &&\qquad k<0 \end{aligned} \right.\]

Expression de la fonction de transfert en f de ce filtre :

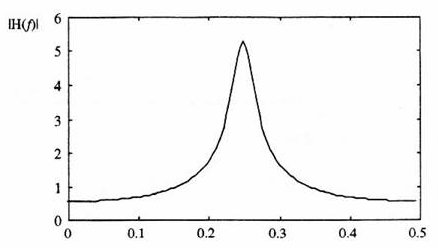En posant \(z=e^{j2\pi f}\) :

\[\begin{aligned} H(f)&=\frac{1}{1-0.81~e^{-j4\pi f}}\\ |H(f)|^2&=\frac{1}{1.656-1.62\cos(4\pi f)}\end{aligned}\]

Le graphe de \(|H(f)|\) est représenté ci-contre.