1. Introduction
On peut utiliser le transistor soit comme un amplificateur, soit comme interrupteur unidirectionnel en courant comme en tension. Dans ce dernier cas, la commande permet d’obtenir :
-
un état conducteur ;
-
un état bloqué.
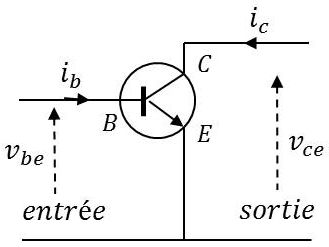 Dans cet article, nous faisons le choix d’un montage en émetteur commun et d’un transistor dans la technologie NPN.
Dans cet article, nous faisons le choix d’un montage en émetteur commun et d’un transistor dans la technologie NPN.
Quatre grandeurs caractérisent le comportement externe du transistor :
-
\(i_b\) et \(v_{be}\) pour le circuit d’entrée ;
-
\(i_c\) et \(v_{ce}\) pour le circuit de sortie.
2. Caractéristiques statiques du transistor
2.1. Caractéristiques d’entrée
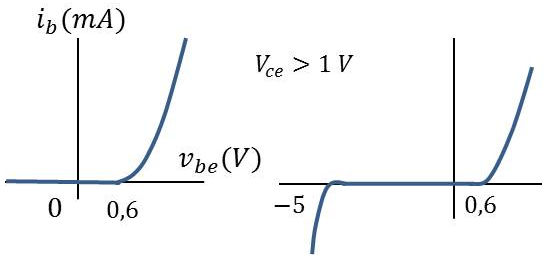 Les caractéristiques \(I_b=f(V_{be})\) sont pratiquement celles d’une diode à jonction PN.
Les caractéristiques \(I_b=f(V_{be})\) sont pratiquement celles d’une diode à jonction PN.
En pratique, pour \(V_{ce}\) > 1 V, la caractéristique d’entrée dépend peu de \(V_{ce}\).
En sens inverse, si la d.d.p. \(V_{be}\) est en module trop grande, il y a claquage de la jonction émetteur-base. Ce claquage est réversible ou irréversible selon le type de transistor utilisé.
Cette d.d.p. est généralement faible ; elle peut varier selon les types entre quelques volts et quelques dizaines de volts.
2.2. Caractéristiques de sortie
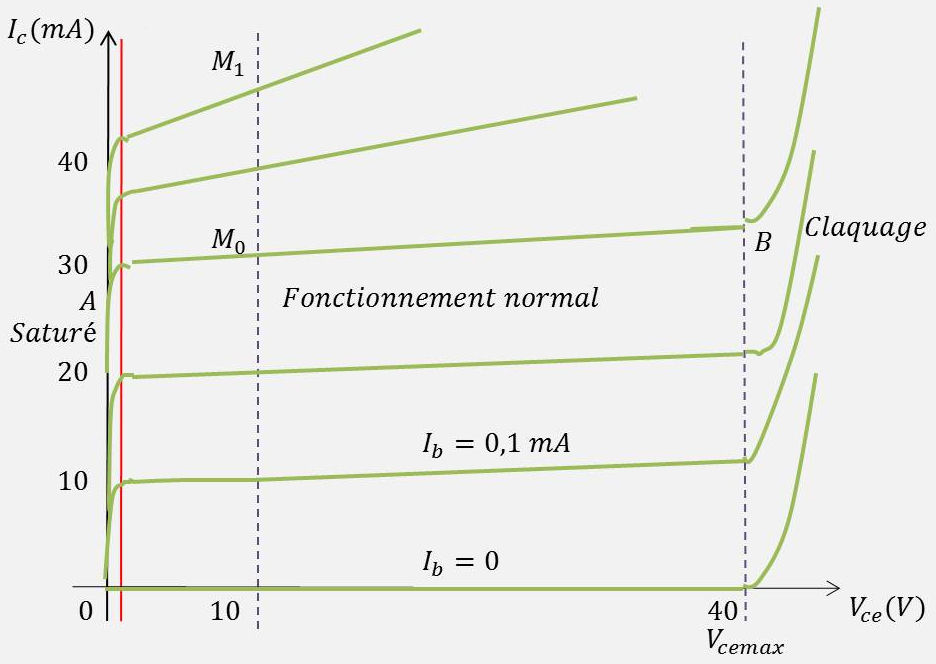 Les caractéristiques statiques de sortie sont fournies sous la forme d’un réseau de caractéristiques \(I_c=f(V_{ce})\) paramétré suivant un ensemble de valeurs de \(I_b\) à savoir \(I_b\) = 0, 0,1 mA, 0,2 mA...
Les caractéristiques statiques de sortie sont fournies sous la forme d’un réseau de caractéristiques \(I_c=f(V_{ce})\) paramétré suivant un ensemble de valeurs de \(I_b\) à savoir \(I_b\) = 0, 0,1 mA, 0,2 mA...
Pour fixer les idées, nous nous intéresserons à une caractéristique de sortie donnée, par exemple celle qui correspond à \(I_b\) = 0,3 mA. Elle se compose de trois parties bien distinctes en fonction de la tension \(V_{ce}\) :
-
0,5 V < \(V_{ce}\) < 40 V : fonctionnement normal
\(I_b\) est constant, les caractéristiques sont presque horizontales.
\(I_c\) dépend peu de \(V_{ce}\).
En réalité, \(I_c\) s’accroît légèrement avec \(V_{ce}\)
-
\(V_{ce}\) > 40 V : valeur importante \(I_c\) croît brusquement.
Le constructeur précise la d.d.p. \(V_{ce~max}\) pour un type donné de transistor.
-
\(V_{ce}\) < 0,5 V : valeur très faible La courbe est pratiquement verticale à l’échelle donnée du graphique.
\(I_c\) dépend alors de \(V_{ce}\), le transistor est alors dit saturé.
 Reprenons à présent le réseau global des caractéristiques avec deux remarques, en supposant que le transistor est en fonctionnement normal.
Reprenons à présent le réseau global des caractéristiques avec deux remarques, en supposant que le transistor est en fonctionnement normal.
On sait que le gain en courant est défini par le paramètre \(\beta\) : \[\beta=\frac{I_c}{I_b}\]
Si \(\beta\) était rigoureusement constant, les caractéristiques de sortie seraient horizontales et équidistantes. En fait, \(\beta\) varie en fonction de \(V_{ce}\) et \(I_c\).
Commentaire
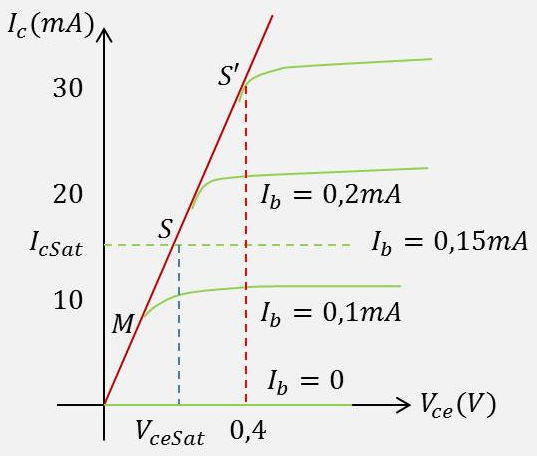
Le point \(S\) est commun à toutes les caractéristiques de sortie telles que \(i_b\) > 0,2 mA. Pour ce point \(S\), on aura : \[I_{csat}=15~{\rm mA}\quad;\quad V_{ce}=0,2~{\rm V}\quad;\quad i_b>0,15~\rm mA\]
3. Transistor bloqué. Transistor saturé
3.1. Transistor bloqué
En première approximation, on peut dire qu’un transistor est bloqué lorsque les courants de base et de collecteur sont négligeables (\(i_b\approx 0\) et \(i_c\approx 0\)). Dans ces conditions, la diffusion des porteurs majoritaires est nulle pour les deux jonctions. Ce qui autorise la définition suivante :
Le transistor est bloqué lorsque les jonctions émetteur-base et base-collecteur sont toutes deux polarisées en inverse.
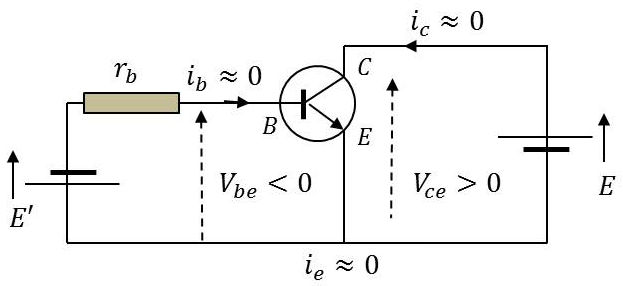 Une jonction PN est polarisée en inverse si la région P est négative par rapport à la région N.
Une jonction PN est polarisée en inverse si la région P est négative par rapport à la région N.
Ainsi, un transistor NPN sera bloqué si : \[V_{be}<0\quad\text{et}\quad V_{cb}>0\]
Pour bloquer un transistor NPN, la d.d.p. \(V_{cb}\) étant positive, il faut que le potentiel de la base soit négatif par rapport à celui de l’émetteur.
Une condition suffisante pour bloquer un transistor NPN : \[V_{be}<0\quad\text{et}\quad V_{ce}>0\]
Comme le montre la figure, il suffit d’inverser la polarité de \(E'\) pour bloquer le transistor. En pratique, il faut que \(E'\) en module n’excède pas \(V_{be}\) inverse max.
3.2. Transistor saturé
 Revenons au réseau de caractéristiques précédent (repris figure ci-contre) sous forme de zoom.
Revenons au réseau de caractéristiques précédent (repris figure ci-contre) sous forme de zoom.
Plaçons-nous à \(i_b\) constant, par exemple \(i_b\) = 0,4 mA, en ne modifiant pas le circuit base. Pour \(V_{ce}\) faible, on constate que la caractéristique de sortie est sensiblement rectiligne, donc \(i_c\) est proportionnel à \(v_{ce}\).
Gardons maintenant \(E=v_{ce}\) constant, par exemple \(v_{ce}\) = 0,2 V, et faisons varier \(i_b\). Deux cas peuvent se produire :
-
\(i_c<I_{c~sat}\)
Le transistor est en fonctionnement normal et \(i_c\) est proportionnel à \(i_b\) : \[i_c=\beta~i_b\]
On peut donc écrire que : \[\beta~i_b<i_{csat}\]
-
Dans le cas contraire, \(i_c\) reste constant et égal à \(i_{csat}\) (point commun \(S\) aux caractéristiques de sortie pour \(i_b\) > 0,15 mA.
Donc le courant \(i_b\) ne contrôle plus le courant \(i_c\), la relation de proportionnalité disparaissant.
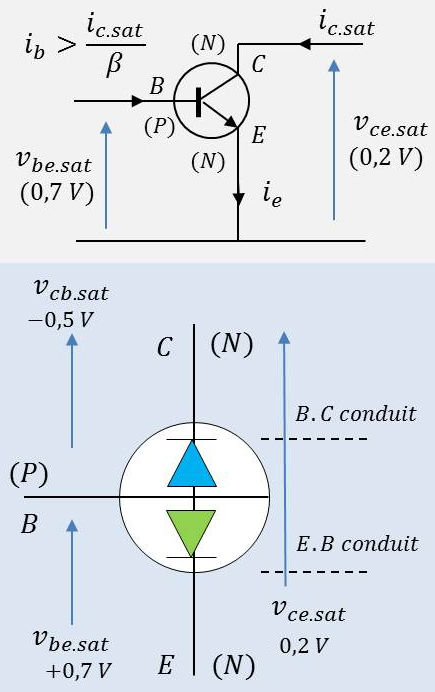 Un transistor saturé est donc caractérisé par \[\beta~i_b~>~I_{c~sat}\]
Un transistor saturé est donc caractérisé par \[\beta~i_b~>~I_{c~sat}\]
Interprétation expérimentale
Un transistor est saturé lorsque les jonctions émetteur-base et base collecteur sont polarisées en sens direct.
Comme la jonction base-collecteur conduit, \(i_c\) dépend de la d.d.p. \(v_{cb}\) aux bornes de cette jonction, donc aussi de \(v_{ce}\).
\(v_{be~sat}\) et \(v_{ce~sat}\) restent faibles. Donc les courants dans un transistor saturé ne sont limités que par le circuit externe dans lequel est inséré le transistor.
La figure ci-contre illustre cette interprétation pour un transistor NPN avec, de plus des valeurs numériques permettant de fixer les idées.
4. Point de repos d’un montage à transistor
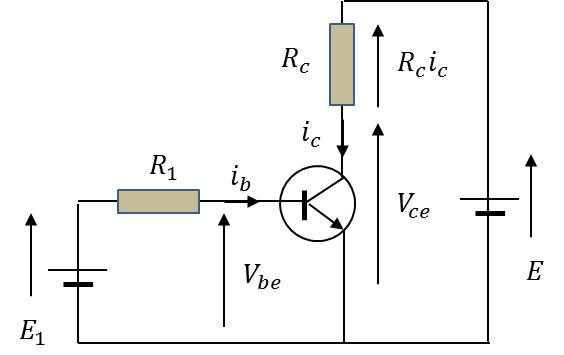 Considérons le montage en émetteur commun NPN représenté figure ci-contre.
Considérons le montage en émetteur commun NPN représenté figure ci-contre.
Les éléments du montage étant donnés, on se propose d’évaluer les courants continus \(i_b\) et \(i_c\), ainsi que les d.d.p. \(V_{be}\) et \(V_{ce}\) à partir des caractéristiques graphiques établies par le constructeur. C’est la méthode la plus simple et la plus courante.
On étudiera donc et respectivement les droites de charge et d’attaque statiques
4.1. Droite de charge statique
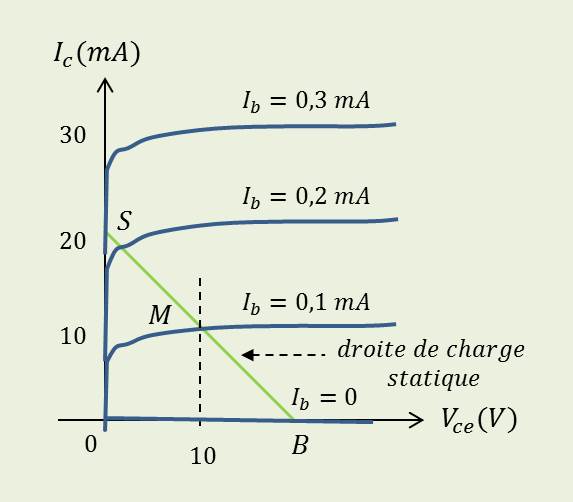 On revient au réseau caractéristique \(I_c=f(V_{ce})\).
On revient au réseau caractéristique \(I_c=f(V_{ce})\).
On peut écrire (circuit collecteur) : \[v_{ce}=E-R_c~i_c\]
Dans le plan (\(i_c,~v_{ce}\)), c’est l’expression de l’équation d’une droite, dite droite de charge statique.
C’est la caractéristique tension-courant du circuit externe au collecteur. Les points d’intersection avec les axes étant respectivement (\(E,~E/R_c\)).
4.2. Droite d’attaque statique
 On peut écrire (circuit de base) : \[V_{be}=E_1-R_1~i_b\]
On peut écrire (circuit de base) : \[V_{be}=E_1-R_1~i_b\]
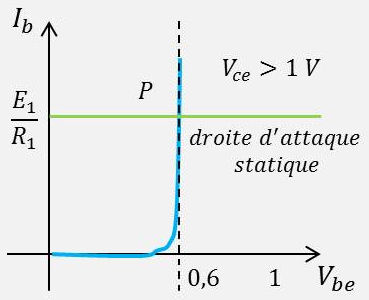
Dans le plan (\(I_b,~V_{be}\)) correspondant aux caractéristiques d’entrée du transistor, c’est l’équation de la droite d’attaque statique.
C’est la caractéristique tension-courant du circuit externe de base. Le point d’intersection avec l’axe des ordonnées étant(\(E_1~/~R_1\)).
Les coordonnées du point d’intersection \(P\) permettent de déterminer \(I_b\) et \(V_{be}\).
En pratique, le plus souvent, avec le montage choisi, la d.d.p. \(v_{be}\) est petite par rapport à \(E\).
La droite d’attaque statique est presque horizontale et le circuit de base se comporte comme un générateur de courant presque parfait : \[I_b~\approx~\frac{E_1}{R_1}\]
4.3. Étude d’un exemple
Nous reprenons le même montage avec les valeurs des composants suivantes :
\[\begin{aligned} &E_1=10~{\rm V}\qquad;\quad E=20~\rm V\\ &R_1=100~{\rm k\Omega}\quad;\quad R_c=1~\rm k\Omega\end{aligned}\]
1) Négligeons \(V_{be}\approx\) 0,6 V par rapport à \(E_1\) = 10 V.
On a alors : \[I_b\approx \frac{E_1}{R_1}\quad\Rightarrow\quad I_b\approx 0,1~\rm mA\]
Le point de repos \(M\) est situé :
-
sur la caractéristique de sortie correspondant à \(I_b\) = 0,1 mA ;
-
sur la droite de charge statique du montage.
Le transistor est alors en fonctionnement normal.
On voit sur le réseau que \(I_c\) = 10 mA et \(V_{ce}\) = 10 V.
2) Supposons maintenant que \(R_1\) = 33 k\(\Omega\), toutes choses égales par ailleurs.
On a alors : \[I_b\approx\frac{E_1}{R_1}=0,3~\rm mA\]
Le point de repos se trouve maintenant en \(S\) : le transistor est saturé. \[I_c=I_{c~sat}\approx\frac{E}{R_c}=20~\rm mA\]
Si \(R_b\) diminue encore, \(I_b\) augmente, mais \(I_c\) reste constant et égal à : \[I_{c~sat}=\frac{E}{R_c}\]
3) Enfin, supposons que \(R_1\) soit reliée à un point dont le potentiel \(E'\) est négatif par rapport au potentiel de l’émetteur.
Le transistor est bloqué. Le point de repos vient en B.
Nous avons alors :
\[\begin{aligned} &I_b\approx 0\qquad;\quad I_c\approx 0\\ &V_{ce}=E\quad~;\quad V_{be}=E'<0\end{aligned}\]

