1. Introduction à la contre-réaction

Pour réduire les distorsions et le bruit, on ajoute à certains étages d’un amplificateur ce que l’on appelle une chaîne de réaction ou de contre-réaction.

Les étages constituant un système à chaîne ouverte sont ainsi transformés en un dispositif à chaîne fermé (ou bouclé). Il s’agit en fait d’un système asservi au sens classique du terme.

Les boucles de réaction permettent normalement d’améliorer les performances d’un amplificateur. Cependant, elles peuvent avoir, dans certains cas, un rôle nuisible.

Elles existent à l’état naturel dans certains systèmes du fait de leur structure interne (ainsi la capacité grille-drain d’un TEC).

2. Principe du système asservi

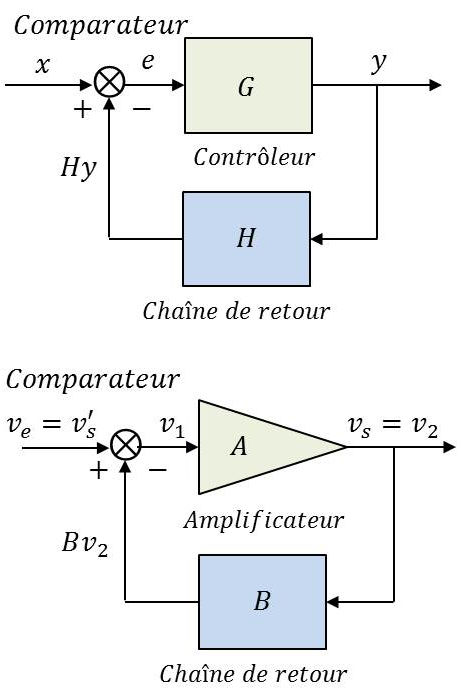Rappelons qu’un asservissement est un système permettant d’assurer la commande d’une grandeur de sortie quelconque (\(y\)) à partir d’une grandeur d’entrée (\(x\)). La grandeur d’entrée \(x\) peut être une d.d.p. La grandeur de sortie \(y\) peut être transformée en une d.d.p. : \[v_r=H~y\]

grâce à une chaîne de retour.

Une application classique : celle de deux tensions appliquées à un organe différentiel ou comparateur négatif. Celui-ci délivre une tension d’erreur : \[e=x-H~y\]

qui agit sur les appareils de commande pour élaborer le signal de sortie.

L’ensemble de ces organes constitue le contrôleur.

Dans le cas de l’électronique, la grandeur à commander est la tension appliquée au récepteur, et au niveau du comparateur il y a superposition du signal de retour sur celui de l’entrée.

Le contrôleur est un amplificateur à un ou plusieurs étages. La chaîne de retour est un réseau passif qui détermine la fraction de la tension de sortie à réinjecter à l’entrée.

3. Montage électronique : réaction et contre-réaction

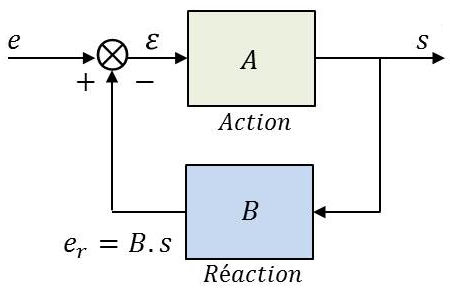Le comparateur appelé encore mélangeur est positif. Si le signal ramené à l’entrée est en phase avec le signal d’entrée, la réaction est positive. Dans le cas contraire, on dit qu’il y a rétroaction ou contre-réaction.

On désigne par \(A\) le gain de la chaîne d’action et par \(B\) celui de la chaîne de réaction.

Faisons l’hypothèse du traitement de signaux sinusoïdaux. En considérant les tensions ramenées par les différentes branches du schéma bloc du système bouclé :

\[\begin{aligned} \varepsilon&=e-e_r\\ s&=B~\varepsilon\\ e_r&=B~s\\ s&=A~\varepsilon\end{aligned}\]

Il vient, tous calculs faits : \[s=\frac{A~e}{1+A~B}\]

À partir de cette relation, on peut exprimer le rapport direct sortie/entrée ou transfert : \[\frac{s}{e}=A'=\frac{A}{1+A~B}\]

Discussion

1) \(1+A~B<1\quad\Rightarrow\quad A'>A\)

La réaction est positive : le système devient instable.

Le signal de sortie croît avec le signal d’entrée et vient contribuer à son augmentation.

La divergence du signal de sortie ne cesse qu’avec l’atteinte de la saturation.

2) \(1+A~B=0\quad\Rightarrow\quad A'\rightarrow\infty\)

Le système se comporte comme un oscillateur : présence d’un signal de sortie en l’absence d’un signal d’entrée.

Cet oscillateur est à priori instable, sauf si la condition théorique est exactement réalisée. \[A~B=-1\]

3) \(1+A~B>1\quad\Rightarrow\quad A'<A\)

La réaction est cette fois négative : le système est à priori stable.

Dans le cas particulier où \(A~B\gg 1\), on a pour le système bouclé : \[A'\approx\frac{1}{A}\]

Le gain ne dépend plus alors de la chaîne d’action, mais de la chaîne de contre-réaction. Si réponse de cette chaîne est linéaire, il en est de même de la réponse du système bouclé.

4. Différents types de contre-réaction

Il peut y avoir contre-réaction en tension ou en courant.

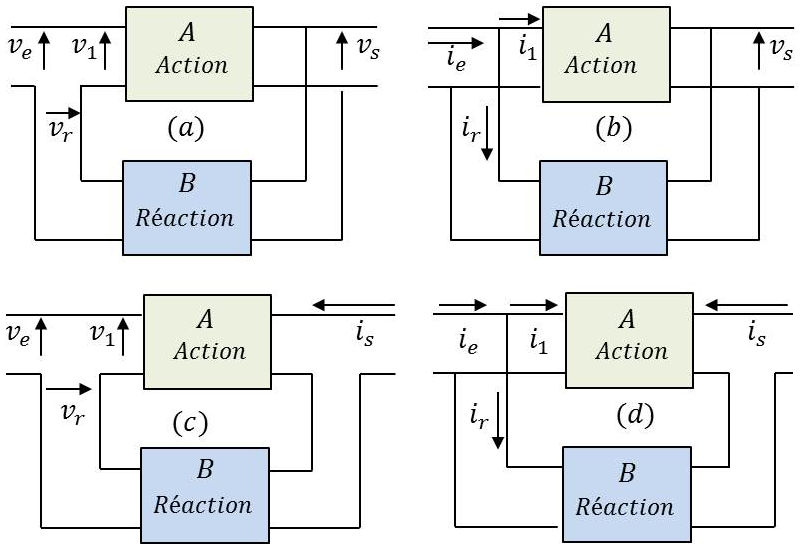Il existe pratiquement quatre types de montages. Ils correspondent aux différents modes d’association de deux quadripôles :

• Tension série (a)

• Tension parallèle (b)

• Courant série (c)

• Courant parallèle (d)

Parmi ces quatre montages nous avons choisi le montage tension série pour une étude électronique plus approfondie. Il s’agit d’ailleurs du montage le plus fréquemment utilisé.

5. Montage tension-série

Nous considèrerons l’amplificateur avec réaction et sans réaction

5.1. Modèle de l’amplificateur sans réaction

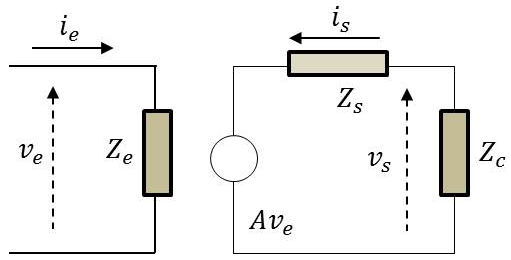Le circuit équivalent (modèle) est représenté ci-contre.

• \(Z_c\) : impédance de charge (ou utile)

• \(Z_e\) : impédance vue à l’entrée

• \(Z_s\) : impédance du générateur de gain \(A\)

Deux relations immédiates :

\[\begin{aligned} v_e&=Z_e~i_e\\ v_s&=A~v_e+Z_s~i_s\end{aligned}\]

5.2. Modèle de l’amplificateur avec réaction

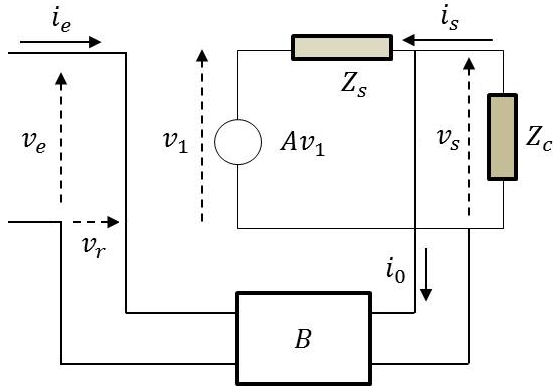On retrouve le modèle précédent auquel on adjoint la chaîne de retour (B).

On fait l’hypothèse que le courant \(i_0\) est extrêmement faible de sorte que l’on peut admettre que : \[Z_s~i_0\approx 0\]

Relations de base : \[\left\{ \begin{aligned} v_s&\approx A~v_1+Z_s~i_s\\ v_s&=-Z_c~i_s\\ v_r&=B~v_s\\ v_e&=v_1+v_r=Z_e~i_e \end{aligned} \right.\]

Tous calculs faits, on obtient la relation : \[v_s=\frac{A}{1+A~B}~v_e+\frac{1}{1+A~B}~Z_s~i_s~\approx~A'~v_e+Z'_s~I_s\]

D’où le schéma équivalent du système bouclé, qui est le même que le précédent, mais avec : \[A~\rightarrow~A'\quad;\quad B~\rightarrow~B'\quad;\quad Z_s~\rightarrow~Z'_s\]

6. Deux exemples classiques de circuits à contre-réaction

6.1. Cellule de Rauch

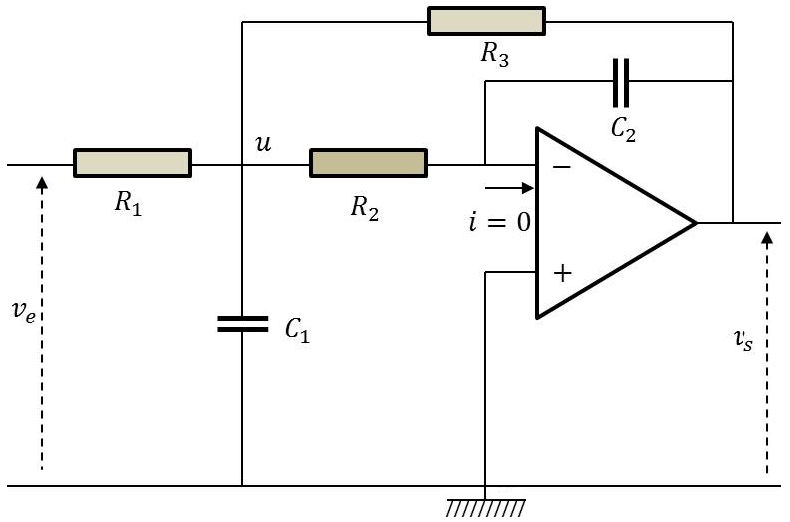Le circuit représenté ci-contre est une cellule de filtrage d’ordre 2 dite de Rauch.

Elle est à contre-réaction multiple et sa fonction de transfert en \(p=j~\omega\) est d’ordre 2 (2 pôles).

Pour établir les équations du circuit, on note que : \[E^+=0\qquad\text{masse réelle}\]

Il faut par ailleurs que : \[E^+-E^-=\varepsilon~\rightarrow~0\]

C’est-à-dire que : \[E^-=0\]

L’entrée de l’amplificateur est au potentiel zéro (masse fictive ou virtuelle).

Répartition des courants : \[i_{R}=i_{R2}+i_{C1}+i_{R3}\quad;\quad i_{R2}=i_{C2}\]

Avec :

\[\begin{aligned} i_{R1}&=\frac{v_e-u}{R_1}\quad;\quad i_{R2}=\frac{u-0}{R_2}\quad;\quad i_{R3}=\frac{u-v_s}{R_3}\\ i_{C1}&=C_1~p~(u-0)\quad;\quad i_{C2}=C_2~p~(0-v_s)\end{aligned}\]

L’élimination du paramètre \(u\) conduit à la fonction de transfert :

\[\begin{aligned} H(p)&=\frac{V_s}{V_e}=\frac{-a}{p^2+b~p+a}\\ a&=\frac{1}{R_1~R_2~C_1~C_2}\quad;\quad \frac{1}{C_1}~\Big(\frac{1}{R_1}+\frac{1}{R_2}+\frac{1}{R_3}\Big)\end{aligned}\]

La présence du signe (–) s’explique physiquement par le fait que le signal entre sur l’entrée \(E^-\) de l’amplificateur opérationnel.

6.2. Cellule de Sallen et Key

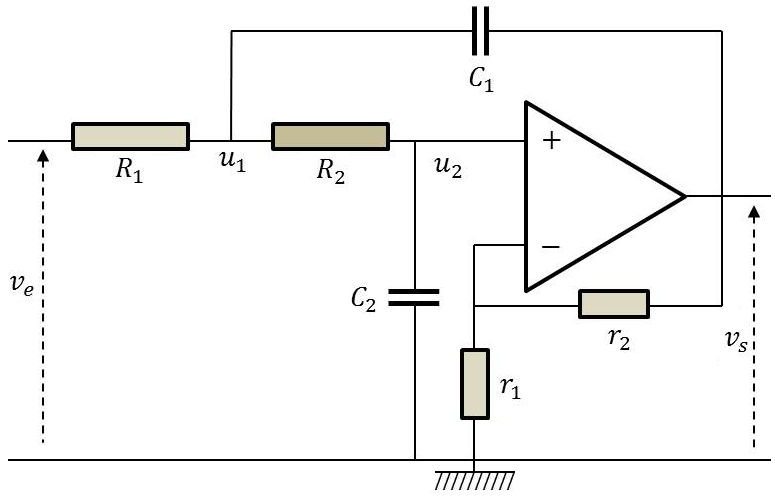La cellule représentée ci-contre est une cellule d’ordre 2 de Sallen et Key.

Elle est dite à source contrôlée, le gain de contrôle (positif) ayant pour expression : \[K=1+\frac{r_1}{r_2}\qquad\text{donc~:}\quad K>1\]

Effet de la source contrôlée : \[v_s=K~u_2\]

Répartition des courants :

\[\begin{aligned} i_{R1}&=i_{R2}+i_{C1} &&i_{R2}=i_{C2}\\ i_{R1}&=\frac{v_e-u_1}{R_1} &&i_{R2}=\frac{u_1-u_2}{R_2}\\ i_{C1}&=C_1~p~(u_1-v_s) &&i_{C2}=C_2~p~(u_2-0)\end{aligned}\]

L’élimination des paramètres intermédiaires \(u_1\) et \(u_2\) conduit à la fonction de transfert : \[H(p)=\frac{V_s}{V_e}=\frac{K}{R_1~R_2~C_1~C_2~p^2+\{R_1C_1~(1-K)+R_2~C_2+R_1~C_2\}~p+1}\]

7. Amélioration des performances par la contre-réaction

La contre-réaction permet d’assurer un gain de valeur constante, indépendante des constituants de la chaîne d’action. De ce fait, elle permet de réduire les distorsions pouvant intervenir et donc d’améliorer les performances du système.

Pour avoir une idée de la façon dont se passe cette optimisation des performances, nous avons choisi deux exemples classiques : la distorsion d’amplitude et la distorsion harmonique.

7.1. Distorsion d’amplitude

On considère la variation relative du gain en fonction de la fréquence (calcul de l’erreur relative) au moyen de la dérivée logarithmique : \[\varepsilon=d(\ln A)=\frac{dA}{A}\]

On revient sur la relation de contre-réaction : \[A'=\frac{A}{1+A~B}\]

Dérivation logarithmique : \[\frac{dA'}{A'}=\frac{dA}{A}-\frac{d(1+A~B)}{1+A~B}=\frac{dA}{A}-\frac{B~dA}{1+A~B}=\frac{dA}{A}~\frac{1}{1+A~B}\]

Du fait de la contre-réaction, on a : \[1+A~B~>~1\]

La formule montre que la contre-réaction contribue à diminuer la distorsion d’amplitude.

7.2. Distorsion harmonique

La distorsion harmonique résulte de la présence de fréquences non désirables, hors du spectre des fréquences du signal d’entrée, conséquences de non-linéarités dues à certains composants du système.

Si on désigne par :

• \(v_e\) : la tension d’entrée du système

• \(v_s\) : la tension de sortie du système

• \(v_d\) : la tension imputable aux défauts

En considérant la somme des deux tensions \(A(v_e-v_s)\) (tension utile) et \(v_d\)(tension de défauts), on obtient, à partir d’un raisonnement analogue au précédent : \[v_s=\frac{A~v_e}{1+A~B}+\frac{v_d}{1+A~B}\]

On voit que la rétroaction contribue à la diminution de la tension parasite en sortie.