1. Capteur dans une boucle à verrouillage de phase

Le capteur peut être utilisé de deux manières :

1. En sortie directe c’est-à-dire sur la charge (moteur). Le système est alors dit en boucle ouverte \(B_o\).

2. Pour un contrôle ou une commande de processus : C’est le cas de la boucle à verrouillage de phase \(B_{\varphi}\).

En boucle ouverte (sans chaîne de retour), la fonction de transfert a pour expression : \[H_o(p)=H_A(p)~H_M(p)\]

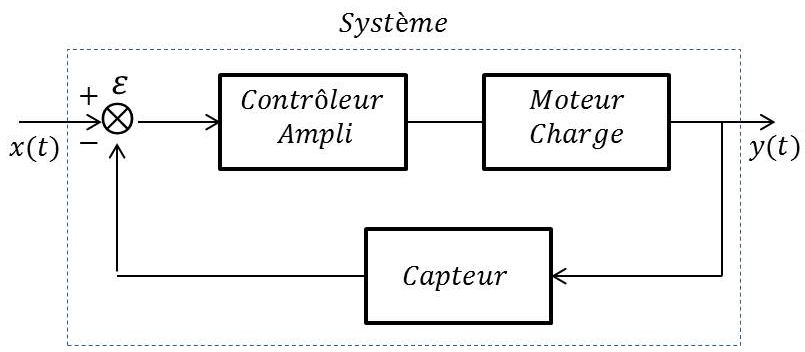Dans le cas de la boucle à verrouillage de phase , la fonction de transfert a pour expression : \[H_{\varphi}(p)=\frac{H_o(p)}{1+H_o(p)~H(p)}\]

\(H(p)\) désignant la fonction de transfert propre du capteur

La constante de temps du capteur (fonction \(H(p)\)) doit être inférieure à la constante de temps du système (fonction \(H_{\varphi}(p)\)) pour que la réponse du système reste stable.

2. Capteurs de proximité (ou de présence)

Il s’agit de détecter la présence d’être vivant dans un champ d’observation donné.

2.1. Capteur par capacitance

Le système repose sur les phénomènes résultant de la coupure des lignes de champ entre deux armatures d’un système condensateur.

On peut imaginer ce condensateur comme constitué par deux plaques ou bien par une ligne (ou une plaque), mais par rapport au sol.

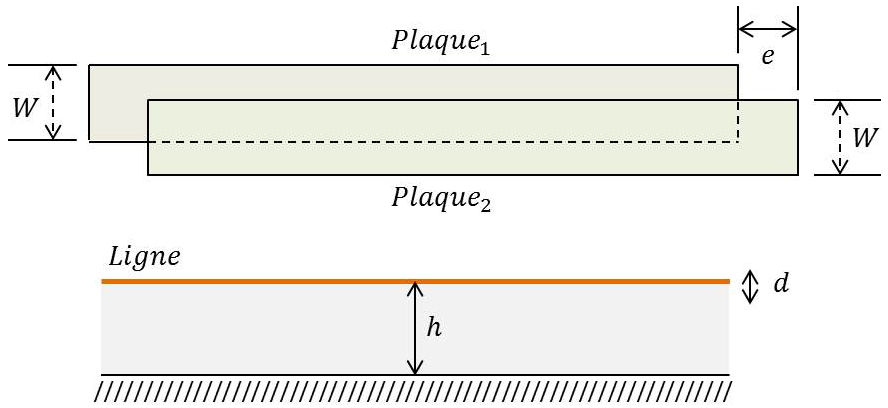Expression de la capacité dans le cas des deux plaques : \[C=\alpha~\frac{e}{W}\]

Expression de la capacité dans le cas de la ligne (ou de la plaque) par rapport au sol : \[C=\beta~\frac{1}{\log\cfrac{4~h}{d}}\]

Un signal appliqué sur la plaque \(P_1\) se retrouve normalement sur la plaque \(P_2\).

En l’absence d’un objet (appellé intrus), le couplage \(P_1/P_2\) est minimal : un faible courant circule alors dans le circuit de sortie. La tension observée sur la charge en sortie est dite réponse de base.

Quand un objet coupe les lignes de champ du condensateur, la capacité change et on observe une variation du signal de couplage.

2.2. Capteur par inductance

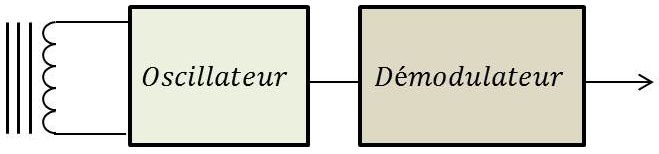Le système est constitué de trois parties :

• une bobine d’induction ;

• un circuit oscillateur ;

• un détecteur de tension (démodulateur).

L’onde de sortie provient de l’oscillateur. Quand le circuit est stabilisé, la forme et l’amplitude de cette onde sont bien déterminées. La réponse est alors dite nominale.

Quand un objet métallique (appelé cible) se présente dans le champ de la bobine, le champ magnétique de la bobine induit des courants dans cette cible. Ces courants engendrent à leur tour un champ magnétique autour de la cible d’où une modification de la réactance de la bobine, d’où une chute brutale de l’amplitude du signal de l’oscillateur.

2.3. Capteur par faisceau lumineux

Le faisceau est émis par un composant électronique (diode électroluminescente par exemple) et détecté par un photo-transistor. Deux formes de détection sont possibles :

• par trajet direct coupé par l’intrus ;

• par trajet avec réflexion sur l’intrus.

2.4. Capteur microonde

La technique est celle du système radar classique : le signal transmis dans l’espace est réfléchi et renvoyé par l’obstacle vers l’antenne réceptrice :

• Le signal reçu est démodulé, filtré, amplifié et maintenu pour être détecté.

• Si son amplitude est supérieure à un seuil donné le système affiche une présence.

• Un premier filtre (50 Hz) élimine les signaux d’interférences venus du voisinage.

• Un deuxième filtre élimine la modulation parasite du signal radar (résidu d’ondulation).

2.5. Capteurs de température

2.5.1. Résistances thermiques

Sous l’effet de la température, un métal s’allonge de sorte que sa résistance électrique croît. En première approximation : \[R_T=R_0~(1+\alpha~\Delta T)\]

Cette linéarité s’applique bien au platine mais il en va autrement des autres métaux.

La relation la plus générale est alors du type : \[R_T=R_0~(1+a_1~T+a_2~T^2+\dots+a_n~T^n)\]

• \(R_T\) : résistance à la température T

• \(R_0\) : résistance à la température de formation de la glace (0 °C)

Deux formes simples peuvent être utilisées (deux gammes de températures) :

\[\begin{aligned} T\in[0~^oC~;~100~^oC]\quad&\Rightarrow\quad R_T=R_0~(1+\alpha~\Delta T)\\ T\in[0~^oC~;~630~^oC]\quad&\Rightarrow\quad R_T=R_0~(1+\alpha~T+\beta~T^2)\end{aligned}\]

À titre documentaire (cas du platinium) : \[\alpha=3,908\times 10^{-3}~\rm K^{-1}\quad;\quad\beta=-5,802\times 10^{-7}~\rm K^{-2}\]

2.5.2. Thermistors

Les thermistors sont des films de carbone (ou de compositions au carbone) obtenus par évaporation.

Les caractéristiques de leur résistance peuvent enregistrer des variations de l’ordre de 4 à 6 % (négatives ou positives).

On appelle résistance froide la résistance qui correspond à la valeur nominale de la résistance à la température de la glace fondante.

Deux expressions équivalentes pour la résistance chaude :

\[\begin{aligned} &R_T=R_0~\{1+\alpha~(T-T_0)\}\\ &R_T=R_0~\exp\Big\{\beta~\Big(\frac{1}{T}-\frac{1}{T_0}\Big)\Big\}\end{aligned}\]

• \(T_0\) : température de référence (\(25^oC\))

• \(T\) : température courante

• \(R_0\) : résistance thermistor à la référence

• \(R_T\) : résistance à la température T

• \(\alpha\) : coefficient de résistance

• \(\beta\) : température caractéristique (1500 K – 7000 K) ; valeur typique : 4000 K

Températures extrêmes : \(T_{min}\)= -200 °C ; \(T_{max}\approx\) +650 °C

2.5.3. Thermocouples

La thermoélectricité a été découverte par Thomas J. Seebeck en 1821.

Une expérience simple : la jonction portée à une certaine température.

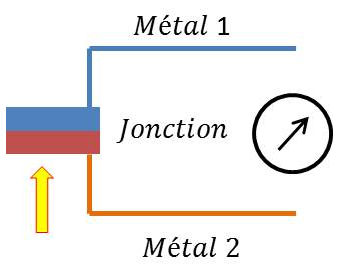La d.d.p. qui apparaît porte le nom de d.d.p. Seebeck. Le potentiel peut varier de 6 à 90 µV K\(^{-1}\).

Il peut être obtenu à partir d’une relation simple : \[dV_S=\alpha_{A,B}~dT\]

• \(V_S\) : potentiel de Seebeck

• \(\alpha_{A,B}\) : coefficient de Seebeck (entre les deux métaux)

• \(T\) : température absolue (en kelvins)

Le coefficient de Seebeck est déterminé de manière empirique.

Il existe d’autre expressions, directes, du potentiel de Seebeck.

2.5.4. Jonctions à semi-conducteur

Une diode est chauffée par une lampe. Un ohmmètre branché à ses bornes indique alors une décroissance très forte de la résistance. Elle constitue donc un bon moyen pour mesurer une température.

Les thermocouples fonctionnent généralement par paires :

• une jonction, utilisée pour la mesure thermocouple ;

• une autre jonction, appelée jonction froide.

Une diode peut être réalisée par court-circuit base – collecteur d’un transistor.

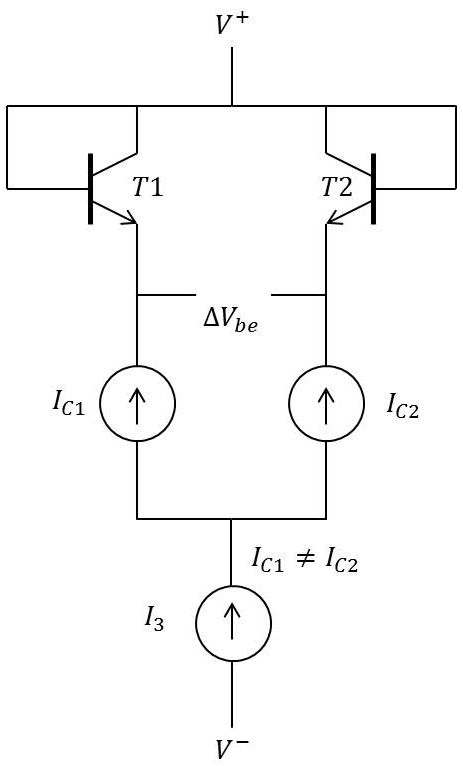
Point important : la tension base-émetteur d’un transistor bipolaire est proportionnelle à la température.

Considérons le montage à deux transistors ci-contre (appelé paire différentielle) : \[\Delta V_{be}=\frac{k~T~\ln(I_{C1}/I_{C2})}{q}\]

• \(k\) : constante de Boltzmann

• \(T\) : température absolue en \(^oK\)

• \(q\) : charge de l’électron

Le rapport \(k/q\) est constant. Le rapport entre les courants peut être maintenu constant par l’introduction d’une source de courant constant \(I_3\). Le seul paramètre variable dans la relation est alors la température \(T\).

3. Capteurs de rayonnement

3.1. Généralités

Un détecteur de rayonnement comporte deux parties principales :

1. la fenêtre d’entrée qui reçoit l’excitation :

   • soit sous forme d’un flux supposé intégralement recueilli par la surface sensible,

   • soit sous forme d’éclairement supposé uniforme et couvrant la totalité de la surface ;

2. les électrodes qui permettent de capter la réponse :

   • une première servant de référence pour les potentiels,

   • une deuxième affectée à l’observation du signal de sortie.

3.2. Cas du rayonnement nucléaire

Les particules parvenant sur le capteur sont caractérisées par :

– Leur énergie cinétique : \[E_c=\frac{1}{2}~m~v^2\]

– Le flux \(\Phi\) (donc la puissance) : \[P=\frac{d}{dt}(E_c)=E~\Phi\]

– La puissance par unité de surface : \[I_R=\frac{P}{S}\]

Le matériau semi-conducteur est privilégié pour ce type de rayonnement. La radiation est absorbée. Le niveau d’absorption varie en fonction du matériau et de l’énergie de la radiation.

3.3. Rayonnements UV, visibles et proche IR

3.3.1. Photoconducteur

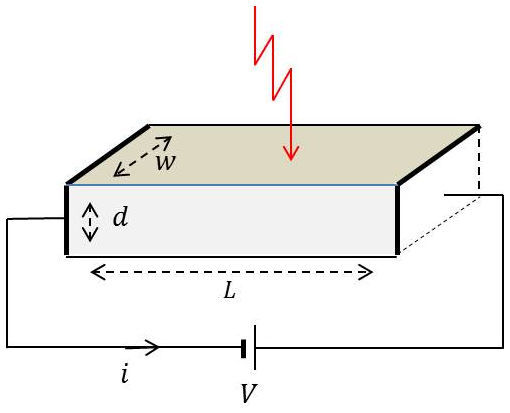La création de paires électrons – trous entraîne une variation de conductivité donc d’une diminution de résistivité : \[\Delta\sigma=e~N~(\mu_n~\tau_n+\mu_p~\tau_p)\]

• \(\mu_n,~\mu_p\) : mobilité des électrons et des trous

• \(\tau_n,~\tau_p\) : durée de vie des porteurs

• \(N\) : nombre de porteurs / unité de volume

Le semi conducteur est généralement du type N : \[\Delta\sigma\approx e~N~\mu_n~\tau_n\]

On démontre que le gain \(A\), nombre d’électrons produits à partir d’un photon ou rapport de la durée de vie de l’électron au temps de transit entre les électrons, est donné par : \[A=\frac{\tau_n}{\tau_T}=\frac{\mu_n~\tau_n~V}{L^2}\]

La variation de résistance est donnée par (loi d’Ohm) : \[\Delta R=k~\frac{1}{\Delta\sigma}~\frac{1}{d}~\qquad~k~:~\text{caractéristique constructeur}\]

3.3.2. Photodiode

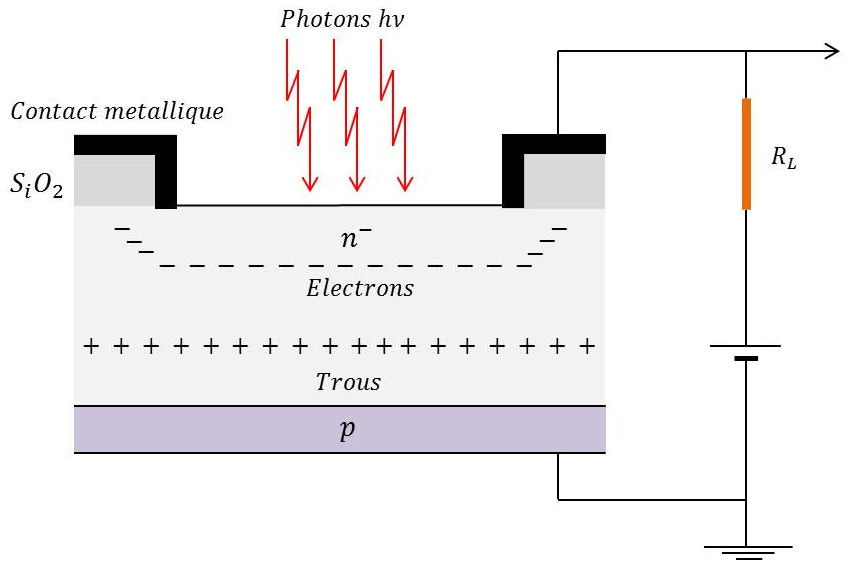Une photodiode est en fait d’une jonction PN. Le photon génère une paire électron – trou dans la zone de déplétion. Ces paires sont ensuite séparées, d’où l’apparition d’un courant électrique.

Ces composants ont une excellente résolution, d’où leur utilisation dans la résolution de problèmes de spectre d’énergie avec une très grande précision.

Elles sont utilisées aussi pour les compteurs à scintillation en raison de leur temps de réponse rapide.

La tension de sortie sur une résistance de charge très élevée (circuit ouvert) est donnée par : \[V_s=\frac{k~T}{e}~\ln\Big(\frac{I_p}{I_s}+1\Big)\]

• \(I_p\) : photocourant, proportionnel à l’éclairement (nombre de photons)

• \(I_s\) : courant de saturation de la photodiode

4. Applications. Capteurs de niveau

4.1. Mesures discrètes

4.1.1. Système à deux électrodes A et B

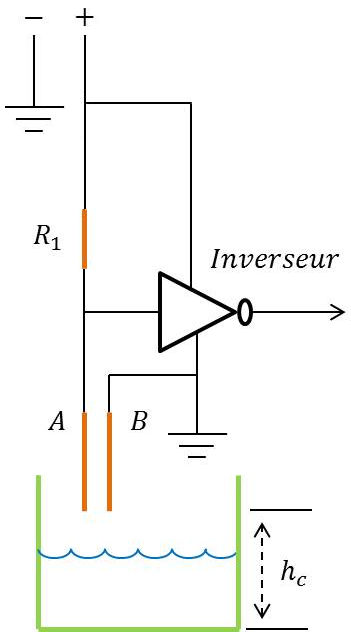Le capteur est un inverseur CMOS.

Tant que le liquide conducteur n’a pas atteint les deux électrodes (circuit ouvert), l’impédance reste très grande, mais au contact : \(R_{AB}~\ll~R_1\).

À une tension forte appliquée en entrée, correspond une tension en sortie extrêmement faible et vice versa.

\[\begin{aligned} V_s\approx 0~~&\Rightarrow~~h<h_c\qquad~h_c~:~\text{hauteur critique}\\ V_s>0~~&\Rightarrow~~\geq h_c\end{aligned}\]

Le problème est celui de la constante de temps \(RC\), dépendant de la valeur de la capacité entre les deux électrodes.

La généralisation à plusieurs électrodes se conçoit aisément.

4.1.2. Système à oscillations contrôlées

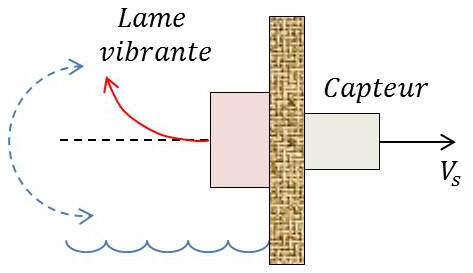Le principe consiste à contrôler les vibrations d’une pale (à l’air libre) reliée à un élément piézoélectrique ou une bobine magnétique.

Quand la pale est au contact du liquide (partiellement ou totalement), ces vibrations sont atténuées ou stoppées.

Le signal de sortie a la même fréquence que la vibration de la pale, mais son amplitude est proportionnelle à l’excursion angulaire de la pale.

4.1.3. Systèmes optiques

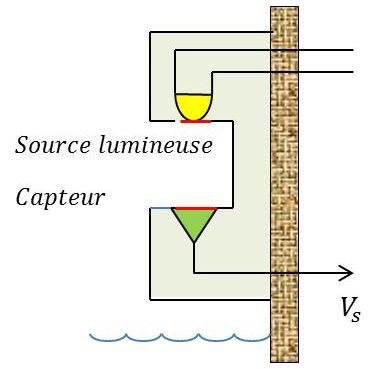Deux types de systèmes optiques :

1) Capteur et source lumineuse sont sur un même support et plaqués sur la paroi de la cuve (type cellule photoélectrique).

Quand le niveau atteint la hauteur critique, le capteur est aveuglé, d’où une modification importante du signal de sortie.

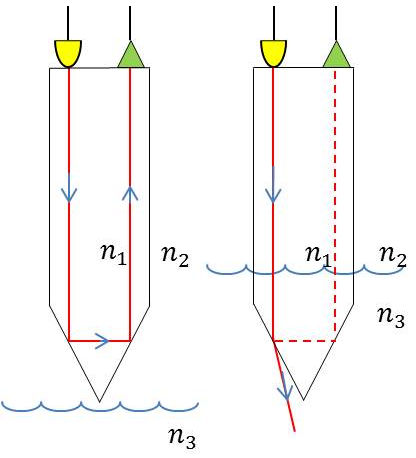2) Capteur à prisme basé sur les propriétés de réfraction et de réflexion totale (loi de Snell) : \[\alpha_r=\sin^{-1}\Big(\frac{n_1~\alpha_i}{n_2}\Big)\]

Réflexion totale au contact prisme – air : le rayon parvient au capteur par la deuxième partie du prisme.

Il n’y a plus de réflexion totale contact du liquide. Le rayon est transmis dans le liquide, la partie revenant vers le capteur est très atténuée et même quasiment nulle.

4.2. Mesures continues

4.2.1. Système par résistance

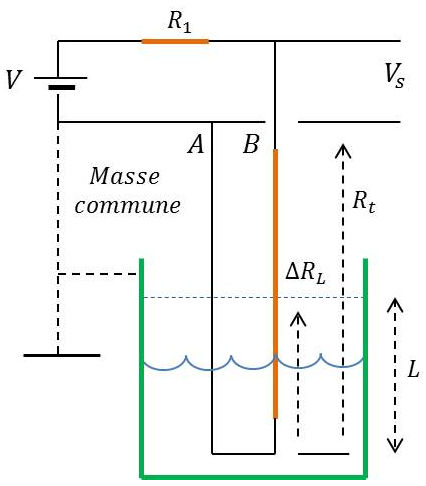L’augmentation de hauteur du liquide conducteur entraîne la diminution de la valeur de la résistance, donc une modification de la tension de sortie du pont diviseur :

\[\begin{aligned} V_s&=V~\frac{R_{t'}}{R_1+R_{t'}}\\ R_{t'}&=R_t-\Delta R_L\end{aligned}\]

La température peut avoir une influence sur la mesure, car : \[R_{t'}\quad\rightarrow\quad R_0~(1+\alpha~T)\]

4.2.2. Système par variation de capacité

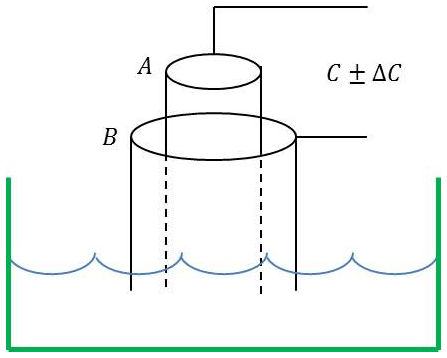L’expression de la capacité d’un condensateur cylindrique est de la forme : \[C=\frac{K}{\log_{10}\cfrac{r_2}{r_1}}\]

On mesure alors le rapport : \[\frac{\Delta C}{C_{ref}}\]