1. Contexte

Cette conférence s’inscrit dans le projet d’enseignement qui a fait l’objet d’une précédente présentation intitulée à l’identique : Filtres électroniques de fréquences passifs. Calcul sur ordinateur : analyse, synthèse et simulation. Elle en est une suite logique (en y faisant d’ailleurs référence si nécessaire).

2. Du filtre passif au filtre actif

Nous avons vu que le filtre passif, composé d’inductances et de capacités, puisait toute son énergie dans le générateur d’entrée, avec une certaine dégradation toutefois si les composants présentent des pertes (généralement de valeur relativement faibles).

Au contraire, le filtre actif, composé d’amplificateurs, de capacités et de résistances (ou éléments équivalents), puise son énergie (perdue par effet joule) dans les alimentations régulées de ces amplificateurs. On comprend qu’il n’est pas possible, dans ces conditions de définir des énergies transmises ou réfléchies par le quadripôle. C’est la raison pour laquelle le filtre actif, contrairement au filtre passif, est étudié sans considération d’adaptation d’impédance.

Le quadripôle est alors assimilable à une cascade de quadripôles élémentaires pour lesquels le paramètre physique intéressant est la tension étudiée entre l’entrée et la sortie, autrement dit les fonctions de transfert propre et respective de chacun de ces quadripôles élémentaires. Chaque quadripôle présente une très forte impédance d’entrée et une très faible impédance de sortie, ce qui autorise le principe d’indépendance de ces quadripôles actifs.

Le seul point commun aux deux types de filtres est le processus de l’approximation permettant de connaître l’ordre du filtre et sa fonction de transfert. L’étude faite dans le cas des filtres passifs est ici transposable. Toute cette partie approximation est supposée connue.

3. Cellule élémentaire du filtre actif

3.1. Cellule d’ordre 1 (passe-bas)

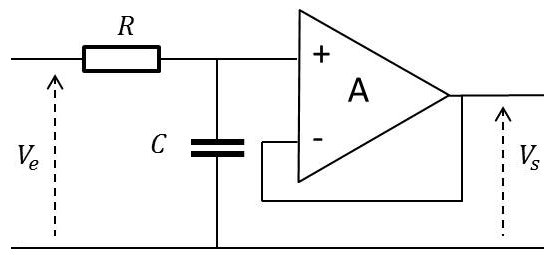Une cellule passe-bas d’ordre 1 est composée d’un simple circuit RC dont le point commun est relié à l’entrée (+) d’un amplificateur opérationnel, l’entrée (–) étant mise en court-circuit avec la sortie. L’amplificateur ainsi monté est dit en suiveur.

L’impédance d’entrée étant considérée comme infinie, aucun courant ne passe vers l’entrée \((+)\) et le circuit est celui du potentiomètre. Ce qui permet d’écrire : \[\frac{V_s}{V_e}=\frac{Z_c}{R+Z_c}\]

D’où la fonction de transfert : \[H(p)=\frac{1/R~C~p}{p+1/R~C~p}=\frac{1}{1+R~C~p}\]

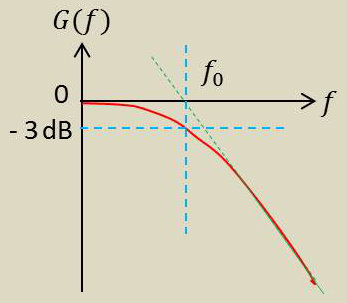
La figure ci-contre représente le graphe de sa réponse harmonique : \[G_{dB}=20~\log_{10}|H(j~\omega|\]

Cette réponse fait apparaître le point remarquable \(P(f_0,~-3)\). On dit que \(f_0\) est la fréquence de coupure à –3 dB.

Explication :

\[\begin{aligned} H(p)&=\frac{\omega_0}{p+\omega_0}\qquad\text{avec :}\quad\omega_0=\frac{1}{R~C}\quad\text{ou}\quad f_0=\frac{1}{2\pi ~R~C}\\ |H(j~\omega)|&=\frac{\omega_0}{\sqrt{\omega_0^2+\omega^2}}\end{aligned}\]

Pour \(\omega=\omega_0\), on voit que \(|H(j~\omega_0)|=1/\sqrt{2}\)

Et on a bien : \[20~\log_{10}|H(j~\omega_0)|=-3~dB\]

3.1.1. Synthèse

La connaissance de la fonction de transfert conduit immédiatement à la valeur de \(f_0\) ou bien encore de \(\omega_0\), donc au produit \(R~C\).

Une relation et deux inconnues \(R,C\) ? C’est une caractéristique propre aux filtres actifs que de disposer de plus d’inconnues que de relations, ce qui donne des degrés de liberté. Très généralement, ce sont les valeurs des capacités que l’on s’impose, les résistances étant alors calculées.

3.1.2. Méthodes d’ajustage

Nous allons supposer à présent que la résistance \(R\) est ajustable, par exemple au moyen d’un potentiomètre, et que la capacité est par contre fixée. Il existe deux méthodes d’ajustage : la méthode d’ajustage en gain et la méthode d’ajustage en phase.

Méthode d’ajustage en gain

On injecte à l’entrée un signal sinusoïdal \(V_e\) de fréquence \(f_0\) et on mesure le signal \(V_s\) obtenu en sortie. On fait varier la résistance \(R\) jusqu’à ce que : \[V_s=\frac{V_e}{\sqrt{2}}\]

On voit qu’il est inutile, dans ces conditions, de prendre une valeur de \(C\) trop précise, donc relativement coûteuse, son imprécision ainsi que l’imperfection de l’amplificateur, voire l’influence de capacité parasites, étant compensées par \(R\) (constante de temps \(\tau=R~C\).

Le réglage, qualifié de dynamique, permet de positionner le point \(P\), donc d’ajuster \(f_0\) à \(-3~dB\), ce qui définit pleinement la fonction \(H(p)\).

Méthode d’ajustage en phase

Au lieu de considérer le module du nombre complexe \(H(j~\omega)\), on peut s’intéresser à sa phase puisque l’objectif reste le réglage de \(f_0\), fréquence de coupure qui définit la courbe à elle seule :

\[\begin{aligned} H(j~\omega)&=\frac{\omega_0}{\omega_0+j~\omega}\\ \varphi&=-\arctan\Big(\frac{\omega}{\omega_0}\Big)\quad;\quad \varphi=\varphi_e-\varphi_s\end{aligned}\]

En choisissant \(\omega=\omega_0\), on aura : \[\varphi=-\arctan(1)=-\frac{\pi}{4}\]

Il suffira d’injecter un signal sinusoïdal de fréquence \(f_0\) en entrée et de faire varier la résistance \(R\) jusqu’à ce que l’on obtienne au phasemètre la valeur (\(-\pi/4\)).

3.2. Cellule d’ordre 2 (passe-bas)

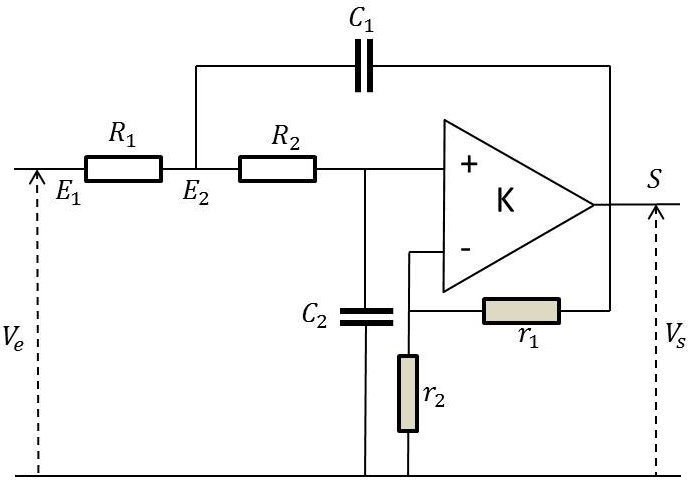Nous prendrons comme modèle de cellule d’ordre 2 la cellule dite de Sallen et Key à source contrôlée (\(r_1,~r_2\)) dont la fonction de transfert a pour expression :

\[\begin{aligned} &H(p)=\frac{K}{R_1~R_2~C_1~C_2~p^2+[(1-K)~R_1~C_1+R_2~C_2+R_1~C_2]~p+1}\\ &K=1+\frac{r_1}{r_2}\quad;\quad K>1\quad \text{(contrôle de source)}\end{aligned}\]

3.2.1. Synthèse

Il n’est pas nécessaire de développer ce paragraphe, ce qui a été expliqué avec la cellule d’ordre 1 se retrouvant ici, la différence tenant au nombre de variables \(R_1,~R_2,~C_1,~C_2,~K\).

On s’impose la valeur de \(K\) qui correspond au gain global à l’origine, indépendamment de l’approximation pour la fonction de transfert. Fixant \(C_1,~C_2\), il reste à calculer \(R_1,~R_2\) à partir des coefficients du polynôme, donc deux relations. Il s’agit bien sûr de valeurs à considérer comme initiales si l’on souhaite procéder par ajustage des constantes de temps \(R_1~C_1,~R_2~C_2\).

Remarques

1) Sous une autre forme qui fait apparaître, non pas des composants, mais des paramètres physiques, cette fonction de transfert peut s’écrire : \[H(p)=\frac{K}{p^2+\omega_0/Q~p+\omega_0^2}\]

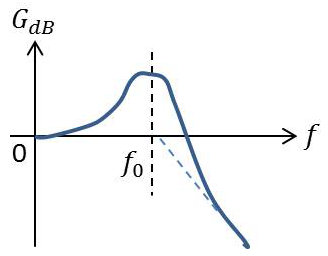\(\omega_0\) est la pulsation de résonance.

\(Q\) est le facteur de surtension qui caractérise l’acuité de la résonance et peut être parfois remplacé par le facteur d’amortissement \(\zeta=1/2~Q\).

Les deux paramètres (\(\omega_0,~Q\)) ou (\(\omega_0,~\zeta\)) suffisent pour caractériser totalement la réponse harmonique. Il faut donc assurer leur ajustage.

2) On profitera de cet exemple pour insister sur la nécessité d’indépendance des réglages (visible sur les coefficients de la fonction de transfert). Les valeurs de capacités sont bien sûr fixées.

On voit tout de suite que :

• les résistances \(R_1,R_2\) permettent d’ajuster \(\omega_0\) ;

• l’une des résistances du contrôle \(K\), soit \(r_1,~r_2\), permet d’ajuster \(Q\) sans perturber l’ajustage précédent de \(\omega_0\).

On notera qu’il s’ensuit une modification \(K\rightarrow K'\) qui est sans incidence, car il s’agit d’un gain global (translation) qui peut être facilement réadapté.

3.2.2. Méthode d’ajustage

Ajustage de \(\omega_0\)

La phase de \(H(j~\omega)\) s’exprime par : \[\varphi=-\arctan~\frac{[(1-K)~R_1~C_1+R_2~C_2+R_1~C_1]~\omega}{1-R_1~R_2~C_1~C_2~\omega^2}\]

La pulsation de résonance théorique est : \[\omega_0=\frac{1}{\sqrt{R_1~R_2~C_1~C_2}}\]

Si on impose au signal entrant la pulsation \(\omega=\omega_0\), on aura : \[\varphi=-\arctan(\infty)=-\frac{\pi}{2}\]

Pour ajuster le paramètre \(\omega_0\), on pourra injecter en \(E_1\), un signal sinusoïdal de pulsation \(\omega_0\), et on règlera \(R_1\) ou \(R_2\) pour obtenir ce déphasage de \(-\pi/2\).

Pour répartir les réglages entre \(R_1\) et \(R_2\), on peut procéder en deux temps :

1. Injecter le signal en \(E_2\), ce qui revient à ajuster la constante de temps \(R_2~C_2\) sur un filtre à un pôle, c’est-à-dire : \[\omega_2=\frac{1}{R_2~C_2}\quad\text{et}\quad \varphi=-\frac{\pi}{4}\]

   On règle ainsi \(R_2\).

2. Injecter ensuite le signal en \(E_1\) et terminer l’ajustage de \(\omega_0\) à \(-\pi/2\).

Ajustage de \(Q\)

Reprenons l’expression de la phase sous la forme : \[\varphi=-\arctan~\frac{B\omega}{1-A~\omega^2}\]

Si l’on choisit par exemple une phase \(\varphi=-\pi/4\), on aura : \[-\frac{B~\omega}{1-A~\omega^2}=-1\qquad\text{ou encore :}\quad A~\omega^2+B~\omega-1=0\]

La racine positive de cette équation est : \[\omega_1=\frac{-B+\sqrt{B^2+4~A}}{2~A}\]

Ainsi, pour ajuster le facteur de surtension \(Q\), on injectera en \(E_1\), un signal sinusoïdal de pulsation \(\omega_1\) (solution de l’équation du second degré), et on règlera \(K\) pour obtenir en sortie un déphasage \(\varphi=-\pi/4\).

3.3. Technique de calcul de la fonction de transfert de structure

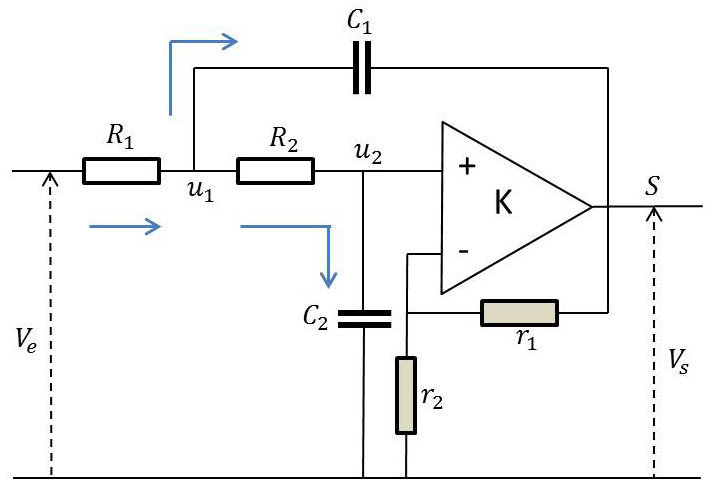
Le calcul sera fait en considérant toujours la structure à source contrôlée de Sallen et Key, mais le processus est tout à fait général.

Rappelons l’expression du gain de contrôle : \[K=1+\frac{r_1}{r_2}\qquad\text{avec}~K>1\]

L’expression de la fonction de transfert peut être retrouvée rapidement à partir de la répartition des courants (aucun courant n’entre dans l’amplificateur) :

\[\begin{aligned} i_{R_1}=i_{R_2}+i_{C_1}\quad&;\quad~i_{R_2}=i_{C_2}\\ i_{R_1}=\frac{V_e-u_1}{R_1}\quad&;\quad~i_{R_2}=\frac{u_1-u_2}{R_2}\\ i_{C_1}=C_1~p~(u_1-V_s)\quad&;\quad~i_{C_2}=C_2~p~(u_2-0)\\ V_s=K~u_2\qquad&\text{contrôle de source}\end{aligned}\]

L’élimination des potentiels intermédiaires \(u_1,~u_2\) conduit à l’expression : \[H(p)=\frac{V_s}{V_e}=\frac{1}{R_1~R_2~C_1~C_2~p^2+[R_1~C_1~(1-K)+R_2~C_2+R_1~C_2]~p+1}\]

4. Ajustage dynamique industriel. Aperçu

4.1. Technologie hybride couche épaisse

Nous avons choisi, pour l’avoir pratiquée, la technologie hybride couche épaisse. Le circuit ressemble à un circuit imprimé de très petites dimensions. Il n’en diffère que par le substrat (céramique), les capacités (petits pavés) et les résistances (rectangles de pâte résistive) enduites par sérigraphie sur ce substrat entre deux conducteurs.

La sérigraphie est réalisée par quelques masquages pendant lesquels on imprime les pistes, les résistances et les plots sur lesquels seront soudés par la suite les capacités et les circuits intégrés.

4.2. Taille laser des résistances

Les premiers ajustages étaient réalisés par jets de sable (années 1970) comme pour la technique de décapage des monuments ou immeubles à restaurer. Le sable a été très vite remplacé par le laser plus précis et moins nocif, toutes précautions prises.

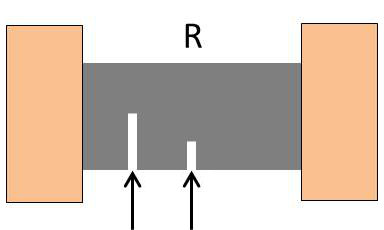
En pratiquant une entaille, on augmente progressivement la valeur de la résistance (étranglement des lignes de courant) jusqu’à ce que la valeur exacte de la constante de temps \((\tau=R~C)\) ait atteint la valeur théorique affichée (contrôle au phasemètre).

L’opération est naturellement irréversible ce qui impose la réalisation d’une résistance initiale bien inférieure à la valeur de synthèse. L’ajustage peut être affiné par la forme de l’entaille ou l’association d’une entaille intermédiaire.

4.3. Le processus industriel. Aperçu

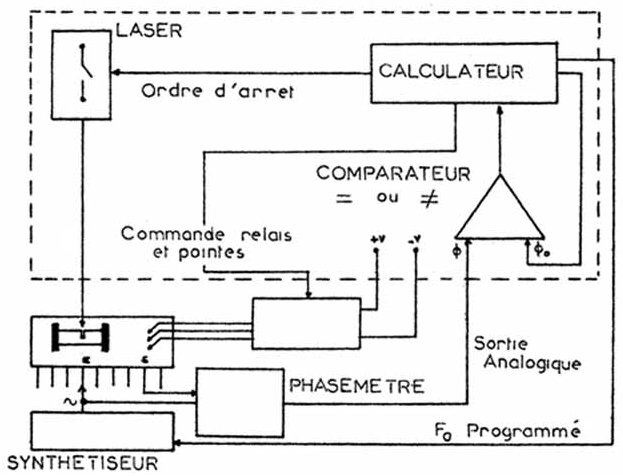Cet ajustage nécessite la création d’une carte à pointes portant des relais commandés par programme de façon à injecter le signal sinusoïdal en un point donné et mesurer la phase (ou l’amplitude) en un autre point donné.

Le système est commandé par un calculateur spécialisé qui acquiert les données \((G/\varphi)\) et donne les instructions de taille au laser.

Selon les caractéristiques du filtre (ordre ou nombre de cellules, raideur dans la bande de transition), l’opération peut prendre de 6 à 15 secondes (chiffres des années 1980).

5. Filtres passe-bande. Une technique particulière

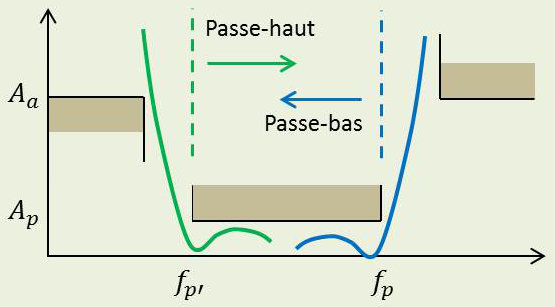Considérons le filtre passe-bande dont le gabarit d’atténuation en fonction de la fréquence est représenté ci-contre. On pourrait :

• déterminer le gabarit du filtre prototype passe-bas ;

• obtenir par une approximation convenue, l’expression de la fonction de transfert (normalisée) de ce prototype ;

• en déduire l’expression de la fonction de transfert réelle (dénormalisation en \(\mathcal{T}~p\) ;

• décomposer en fonctions élémentaires d’ordre 2 (présence d’une cellule d’ordre 1 si l’ordre du filtre est impair).

Cependant, cette méthode contraint a une certaine symétrie liée aux approximations classiques étudiées : raideurs identiques dans les deux bandes de transition, donc obligation de faire le choix de la plus grande raideur (incidence sur l’ordre du filtre). Par ailleurs, l’expression de la fonction de transfert globale serait plus lourde et les les structures élémentaires peuvent plus délicates à calculer, réaliser et ajuster.

Les problèmes d’adaptation d’impédance ne se posent pas. La méthode la plus simple consiste alors à considérer le filtre passe-bande comme la mise en cascade de deux filtres : un filtre passe-bas (fréquence de coupure \(f_{p'}\) et un filtre passe-haut (fréquence de coupure \(f_p\)) :

1. on calcule le filtre passe-bas de manière classique (normalisation et dénormalisation de la fonction de transfert) ;

2. on détermine le filtre passe-bas prototype normalisé puis on effectue la dénormalisation en \(\mathcal{T}~p\) pour revenir au réel passe-haut.

Cette méthode nécessite néanmoins une certaine vigilance du fait de l’indépendance de calcul des deux quadripôles. Dans la bande passante, et dans le cas d’approximations à ondulations, des différences de phase peuvent faire que les ondulations, au lieu de se compenser voire dans les meilleures conditions de se détruire, se trouvent en état de superposition. D’où un risque d’augmentation de \(A_p\).