1. Notion de filtre

Une grande analogie existe entre l’oscillateur mécanique et le filtre électrique. Le filtre électrique est avant tout un oscillateur électrique qui réagit à un signal de fréquence donnée.

Supposons que l’on veuille isoler une fréquence déterminée dans un courant complexe contenant un grand nombre de fréquences, par exemple un courant non sinusoïdal comprenant un fondamental et une infinité d’harmoniques.

On peut utiliser dans ce but les propriétés de résonance d’un oscillateur à 1 degré de liberté.

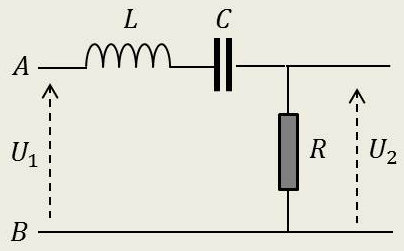
Le montage de la figure ci-contre montre comment séparer pratiquement, aux bornes de la faible résistance, une tension sinusoïdale de pulsation égale à la pulsation de résonance du circuit \(\omega=1/\sqrt{L~C}\) et cela d’autant mieux que la surtension de ce circuit est plus élevée.

Cherchons maintenant à isoler toute une bande de fréquence. Nous pourrions toujours utiliser un circuit du même type, mais à résonance moins aiguë. Cependant, le filtrage serait moins bon.

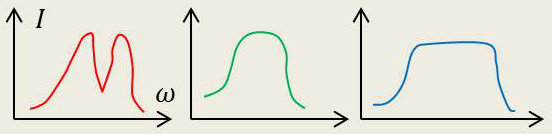Il est alors préférable d’utiliser un système couplé qui, pour un certain rapport couplage – amortissement, présente une courbe à méplat, c’est-à-dire une réponse à peu près invariable dans une bande de fréquences assez large.

\(I\) représente l’intensité secondaire pour une tension primaire donnée.

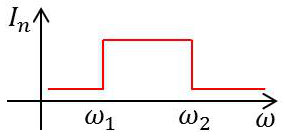On devine qu’en utilisant un oscillateur à n degrés de liberté présentant n fréquences de résonance(chaîne d’oscillateurs), et pour un amortissement convenable, il sera possible d’obtenir une courbe ayant la forme idéale (mais qui reste toutefois théorique).

\(I_n\) est l’intensité dans le dernier oscillateur pour une tension d’attaque donnée dans le premier oscillateur.

Cherchons à résoudre le problème suivant : Intercaler entre un générateur débitant une tension sinusoïdale \(U\) de pulsation \(\omega\) et une impédance d’utilisation \(Z_u\) un appareil qui présente les propriétés suivantes : Pour \(\omega\) compris dans une bande de pulsation déterminée (bande passante), l’introduction de l’appareil ne modifie pas l’impédance sur laquelle est fermée le générateur.

Tout se passe comme si \(Z_u\) était directement branchée à ses bornes. Par contre, pour \(\omega\) extérieur à la bande passante, l’impédance \(Z_u\) ne reçoit plus de courant. L’appareil étouffe en quelque sorte les fréquences extérieures à la bande passante.

Cet appareil que nous désignons sous le nom de filtre sera constitué par une chaîne d’impédances série \((s)\) et dérivation \((d)\) montées comme indiqué par le schéma de la figure ci-contre.

Le montage est obtenu en joignant borne à borne un certain nombre de cellules, la dernière étant fermée sur l’impédance \(Z_u\), la première directement branchée au générateur débitant la tension \(U\)

2. Impédance itérative ou caractéristique

Quel que soit le nombre de cellules intercalées entre l’impédance d’utilisation \(Z_u\) et le générateur, ce dernier doit toujours être fermé sur une impédance égale à \(Z_u\) (impédance vue par le générateur).

Une première condition, triviale : ceci doit être vrai lorsque l’on intercale une seule cellule.

En ne considérant par exemple que la seule dernière cellule et l’impédance \(Z_u\), on voit que cette impédance \(Z'\) a pour expression : \[Z'=\frac{s}{2}+\cfrac{1}{\cfrac{1}{d}+\cfrac{1}{\cfrac{s}{2}+Z_u}}\]

On a alors : \[Z'=Z_u\quad\Rightarrow\quad Z_u-s/2=\frac{d~(s/2+Z_u)}{d+s/2+Z_u}\]

Tous calculs faits, on obtient : \[Z'=Z_u=\sqrt{s~d+s^2/4}=Z_i\]

Supposons alors que le filtre complet soit fermé sur l’impédance \(Z_i\).

En remplaçant l’ensemble (dernière cellule \(Z_i\)) par la simple impédance \(Z_i\) qui lui est équivalente, nous obtenons un filtre présentant une cellule de moins. Il suffit de recommencer autant de fois qu’il y a de cellules pour arriver en définitive à placer finalement \(Z_i\) aux bornes du générateur.

L’ensemble du filtre est équivalent, au point de vue de l’impédance sur laquelle est fermée le générateur, à la simple impédance \(Z_i\) quel que soit le nombre de cellules. C’est bien le résultat que nous voulions obtenir.

3. Courant de branches série et d’impédance terminale

3.1. Équation du second degré caractéristique

Supposons désormais le filtre fermé sur son impédance itérative.

Pour qu’un filtre laisse passer sans affaiblissement le courant sinusoïdal d’une fréquence bien déterminée fourni par le générateur, il faut poser une seconde condition : Toutes les branches série, ainsi que l’impédance terminale \(Z_u\), doivent être parcourues par des intensités égales en module (régime permanent) : \[|I|=|I'|=|I"|=\dots\]

 

 

 

Désignons par :

• \(U',~U'',~\dots\) les potentiels aux nœuds \((s-d)\) (fil de retour pris comme origine des potentiels) ;

• \(i,~i',~i'',~\dots\) les courants dans les impédances \(d\) (les sens positifs étant ceux de la figure).

Remarquons que l’impédance à droite de chaque nœud est \(s/2+Z_i\). On a donc : \[\begin{aligned} U&=I~(s/2+Z_i)\\ U'&=I'~(s/2+Z_i) \end{aligned} \quad;\quad \frac{U}{U'}=\frac{I}{I'}\qquad[1]\]

D’autre part :

\[\begin{aligned} U'&=i~d&&[2]\\ U-U'&=s~I&&[3]\\ i&=I-I'&&[4]\end{aligned}\]

De ces quatre équations, on tire :

\[\begin{aligned} \frac{U-U'}{U'}=\frac{s~I}{(I-I')~d}&=\frac{I-I'}{I'}\\ (I-I')^2-\frac{s}{d}~I~I'&=0\\ \Big(\frac{I}{I'}-1\Big)^2-\frac{s}{d}~\frac{I}{I'}&=0\end{aligned}\]

D’où l’équation : \[\Big(\frac{I}{I'}\Big)^2-2~\Big(1+\frac{s}{2~d}\Big)~\frac{I}{I'}+1=0\qquad[5]\]

Cette équation du second degré en \(I/I'\) permet de déterminer le rapport des intensités circulant dans deux impédances successives.

Par hypothèse, ce rapport doit être de module unité, donc exprimable sous une forme \(\exp(j~\alpha)\). La fonction \(\exp(j~\alpha)\) est alors solution de : \[\exp(2~j~\alpha)-2~\Big(1+\frac{s}{2~d}\Big)~\exp(j~\alpha)+1=0\]

ou encore : \[\frac{\exp(j~\alpha)-\exp(-j~\alpha)}{2}=\cos\alpha=1+\frac{s}{2~d}\]

Le cosinus de \(\alpha\) devant être réel et compris entre \(-1\) et \(+1\), on doit donc avoir : \[\frac{s}{d}\in\mathbb{R}\qquad;\qquad -1~\leq~1+\frac{s}{2~d}~\leq~+1\]

ou encore : \[\frac{s}{d}\in\mathbb{R}\qquad;\qquad -1~\leq~\frac{s}{4~d}~\leq~0\]

Les intensités dans les branches successives sont toutes de même module, deux intensités successives étant déphasées de \(\alpha\), angle constant.

3.2. Bande passante. Fréquence de coupure

Nous désignons sous le nom de bande passante l’intervalle de pulsation \(\omega\) (s’il existe) pour lequel le rapport \(s/4~d\) est réel, négatif et supérieur à (\(-1\)).

Notons que, pour chaque pulsation de la bande passante, l’impédance \(Z_i\) d’utilisation devra être réglée à la valeur \(\sqrt{s~d+s^2/4}\) qui par exemple pourra souvent s’annuler aux frontières du filtre (ceci n’étant d’ailleurs nullement une règle absolue).

On entend par fréquences de coupures, les fréquences correspondant aux extrémités de la bande passante.

Pour les fréquences comprises dans le domaine défini par la bande passante, les intensités à la sortie et à l’entrée du quadripôle ont même valeur, seule la phase ayant changé. À l’extérieur de la bande passante, l’intensité diminue, mais sa phase ne varie pas.

Ainsi, en choisissant un nombre convenable de quadripôles, est-il possible de réaliser l’affaiblissement désiré, à l’extérieur de la bande passante.

Si l’affaiblissement d’une cellule est \(m_1=\exp(\varphi)\) pour \(n\) cellules composant le filtre, il a pour valeur \(m=\exp(n~\varphi)\).

4. Applications. Exemples de filtres élémentaires

4.1. Exemples de non-filtres

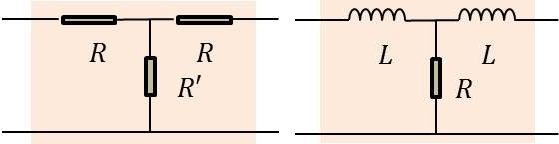Dans le premier circuit de la figure ci-contre, \(s\) et \(d\) sont des résistances ohmiques. Le rapport \(s/d\) est réel mais positif. Aucune fréquence ne passe sans atténuation.

Dans le deuxième circuit, \(s\) ou \(d\) est une résistance ohmique mais \(s/d\) est complexe. Aucune fréquence ne passe sans atténuation.

Dans ces deux exemples, il ne s’agit donc pas de filtres à proprement parler.

4.2. Exemples de filtres réels

4.2.1. Filtre passe-bas

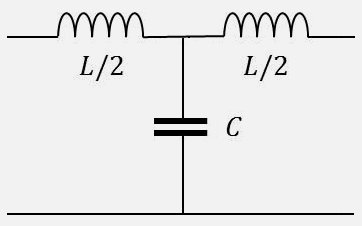Dans le cas de la figure ci-contre, on a : \[s=j~L~\omega\quad;\quad d=\frac{1}{j~C~\omega}\quad\Rightarrow\quad\frac{s}{4~d}=-\frac{L~C~\omega^2}{4}\]

Sachant par ailleurs que \(1+\cfrac{s}{4d}\in\mathbb{R}~>0\), on doit donc avoir : \[L~C~\omega^2\leq 4\qquad\text{donc :}\quad\omega_0\leq\frac{2}{\sqrt{L~C}}\]

C’est la pulsation de coupure de ce filtre passe-bas.

4.2.2. Filtre passe-haut

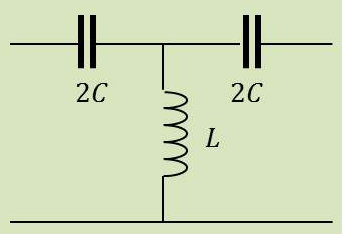Dans le cas dual du précédent (\(L~\leftrightarrow~C\)), on a : \[s=\frac{1}{j~C~\omega}\quad;\quad d=j~L~\omega\quad\Rightarrow\quad\frac{s}{4~d}=-\frac{1}{4~L~C~\omega^2}\]

Sachant par ailleurs que \(1+\frac{s}{4d~}\in\mathbb{R}~>0\), on doit donc avoir : \[L~C~\omega^2>\frac{1}{4}\qquad\text{donc :}\quad \omega_0>\frac{1}{2~\sqrt{L~C}}\]

C’est la pulsation de coupure de ce filtre passe-haut.

4.2.3. Filtres passe-bande

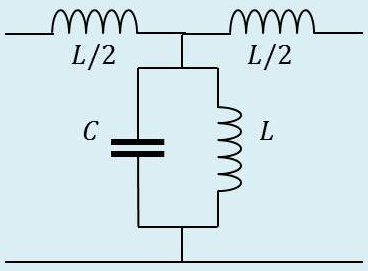Parmi les possibilités de filtres passe-bande, considérons le cas de la figure ci-contre : \[s=j~L~\omega\quad;\quad d=\frac{1}{j~C~\omega+\cfrac{1}{j~L~\omega}}=\frac{j~L~\omega}{1-L~C~\omega^2}\]

On a donc : \[\frac{s}{4~d}=\frac{1-L~C~\omega^2}{4}\]

En introduisant comme précédemment la relation de \(s\) à \(d\), on doit avoir simultanément :

\[\begin{aligned} 1-L~C~\omega^2\leq 0\quad&\Rightarrow\quad\omega\geq\frac{1}{\sqrt{L~C}}\\ 1-L~C~\omega^2\geq -4\quad&\Rightarrow\quad\omega\leq\sqrt{\frac{5}{LC~}}\end{aligned}\]

Ce sont les pulsations de coupure d’un filtre passe-bande : \[\omega_1=\frac{1}{\sqrt{L~C}}\quad;\quad\omega_2=\sqrt{\frac{5}{L~C}}\]

5. Problème réel du filtrage

Nous avons en fait obtenu la condition pour qu’un filtre laisse passer sans affaiblissement le courant sinusoïdal d’une fréquence bien déterminée fourni par le générateur. Il suffit pour cela que \(\omega\) soit comprise dans la bande passante et que l’impédance d’utilisation soit égale à l’impédance itérative, elle-même définie lorsque \(\omega\) est bien définie.

Toutefois, si nous voulons séparer dans un courant complexe les fréquences comprises entre deux limites \(f_1\) et \(f_2\), il ne suffit pas de construire un filtre de coupure \(f_1\) et \(f_2\) pour que la théorie ci-dessus soit rigoureusement applicable.

En premier lieu, le filtre n’aura qu’un nombre fini de cellules. En outre, nous serons obligés de fermer le filtre sur un élément dont l’impédance ne saurait varier avec la pulsation \(\omega\) comme la quantité \(\sqrt{s~d+s^2/4}\).

Au mieux, nous pourrions fermer le filtre sur un élément qui présente une impédance exactement égale à l’impédance itérative pour la fréquence moyenne à passer.

Pour les fréquences situées sur les bords de la bande passante, l’impédance de fermeture ne sera pas égale à l’impédance itérative, et il se produira des réflexions aux extrémités.

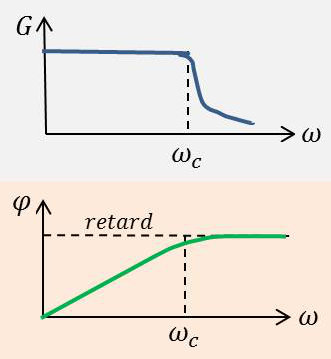
L’affaiblissement en conséquence ne sera pas rigoureusement nul à l’intérieur de la bande passante ; la réponse du filtre variera avec la fréquence suivant la courbe ci-contre qui différera d’autant moins de la courbe théorique rectangulaire que le filtre sera mieux étudié (en particulier grand nombre de cellules, 5 ou 6 au moins, et utilisation de selfs et de capacités à grande surtension).

Remarque (adaptation d’impédance)

Si l’impédance pratique sur laquelle on veut utiliser le courant filtré n’est pas égale à l’impédance itérative, on pourra utiliser des artifices divers pour adapter le filtre à cette impédances d’utilisation.

6. Un filtre particulier : la ligne à retard

Dans ce qui précède, nous nous sommes intéressés à l’affaiblissement en intensité, produit par un filtre. Nous avons également montré qu’à l’intérieur de la bande passante le filtre modifiait la phase.

À l’identique de l’étude des phénomènes de résonance, on représente séparément en fonction de la fréquence la courbe de l’amplitude (gain ou affaiblissement) \(G\) et la courbe de phase \(\varphi\).

Cette variation de la phase, à l’intérieur de la bande passante, ne présente pas systématiquement un inconvénient. Elle peut être même une nécessité.

On peut en particulier assurer une bonne transmission des signaux lorsque l’amplificateur, autrement dit le filtre, provoque un déphasage proportionnel à la pulsation. En effet, appliquons à l’entrée d’un filtre passe-bas un signal périodique non sinusoïdal à transmettre intégralement. Nous décomposons ce signal en série de Fourier et nous supposons que la fréquence de coupure du filtre est supérieure à la fréquence du dernier harmonique de la série.

On a, à l’entrée : \[i_e=I_0+I_1\sin(\omega~t+\varphi_1)+I_2\sin(\omega~t+\varphi_2)+\dots\]

Soit \(\varphi=\omega~\tau\) le déphasage introduit par la cellule. L’intensité n’étant pas modifiée, le courant de sortie a pour expression : \[i_s=I_0+I_1\sin[\omega~(t-\tau)+\varphi_1]+I_2\sin[\omega~(t-\tau)+\varphi_2]+\dots\]

Le signal de sortie n’est pas déformé. Il a la valeur qu’avait le signal d’entrée au moment \((t-\tau)\). Le signal n’a fait que subir un retard lors de son passage dans le filtre.

Note

À titre indicatif et s’agissant du tout premier filtre passe-bas étudié plus haut, un rapide calcul montre que la phase \(\varphi\) s’obtient à partir de l’expression : \[\cos\varphi=1-\frac{L~C~\omega^2}{2}\]

Le calcul montre que :

\[\begin{aligned} &\omega=0&&\cos\varphi=1&&\varphi=0\\ &\omega=\omega_c=\frac{2}{\sqrt{L~C}}&&\cos\varphi=-1&&\varphi=\pi\\ &\omega=\frac{\omega_c}{2}=\frac{1}{\sqrt{L~C}}&&\cos\varphi=0,5&&\varphi=\frac{\pi}{3}\end{aligned}\]

Au-delà de la bande passante (\(\omega>2/\sqrt{L~C}\)), la phase est constante (\(\varpi=\pi\)), mais le gain \(G\) varie.