1. Introduction à la jonction PN

Les diodes de redressement de tensions alternatives sont formées par la juxtaposition, la jonction de deux domaines d’un même semi-conducteur, l’un de type P, l’autre de type N.

Les impuretés généralement employées pour obtenir des semi-conducteurs sont :

• type P : B, Al, Ga, Ti (Mendeleiev III° colonne) ;

• type N : P, As, Sb, Bi (Mendeleiev V° colonne).

Pour citation, les trois méthodes employées pour préparer une jonction : par tirage de cristal, par alliage et par diffusion.

2. Prévision de la théorie des bandes

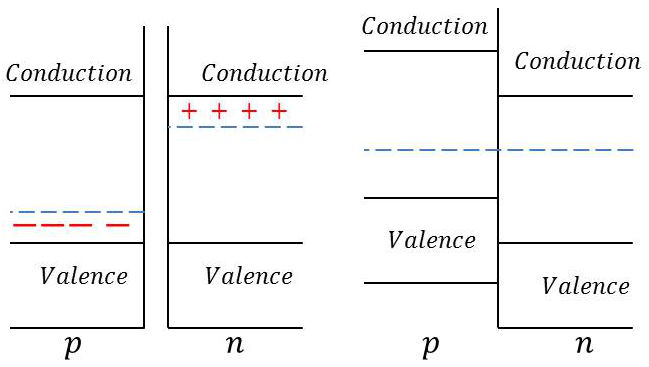
Pour fixer les idées considérons une jonction PN au Ge (propos généralisables). La région P et la région N, séparées par la jonction, sont constituées de germanium. Leurs bandes de valence et de conduction sont donc les mêmes.

Une différence essentielle, sur laquelle repose le fonctionnement de la diode : de par l’existence de niveaux accepteurs (région P) et des niveaux donneurs (région N), l’énergie de Fermi d’un échantillon de Ge P est inférieure à celle d’un échantillon de Ge N tant que les échantillons sont séparés.

Par contre, en établissant un contact étroit, une jonction, il y aura égalisation des énergies de Fermi de la région P et de la région N, condition nécessaire à l’équilibre thermique.

S’il n’en était pas ainsi, les probabilités de Fermi resteraient inégales et des électrons passeraient de la région P à la région N jusqu’à établir cette égalité des niveaux.

D’où des translations égales des bandes de valence et de conduction :

• vers le haut pour la région P ;

• vers le bas pour la région N.

De ces translations, nécessaires à l’égalisation des niveaux de Fermi (cf. fig.), résulte une barrière de potentiel de hauteur \(V_0\) qui fait apparaître une dissymétrie électrique dans la jonction PN et permet d’expliquer la forme de la caractéristique (courant, tension) d’une jonction.

3. Barrière de potentiel

3.1. Interprétation physique

Le niveau de Fermi se présente comme une prévision thermodynamique de l’existence de la barrière de potentiel \(V_0\), mais sans expliquer, en détail comment elle se forme. C’est le phénomène de diffusion des trous de la région P, où ils sont en excès, vers la région N et naturellement celle des électrons de la région N, où ils sont en excès, vers la région P qui est à l’origine de cette barrière de potentiel.

La théorie de la diffusion permet de calculer \(V_0\) en fonction des concentrations \(N_a\) en atomes accepteurs (région P) et \(N_d\) en atomes donneurs (région N). L’expression de la densité \(J_n\) de courant électrique dû aux électrons contient deux termes : \[\overrightarrow{J_n}=e~\mu_n~n~\overrightarrow{E}+e~D_n~\overrightarrow{\rm grad}~n\qquad[1]\]

Le premier dû au transport des électrons sous l’action du champ électrique \(\overrightarrow{E}\). Le second dû à la diffusion \(D_n\) des électrons vers les régions où N est faible. Même raisonnement et équations analogues pour les trous.

À l’équilibre thermodynamique (plus de courant à travers la jonction) : \[\overrightarrow{J_n}=\overrightarrow{0}\quad;\quad\overrightarrow{J_p}=\overrightarrow{0}\qquad[2]\]

Partant de l’ensemble des relations maintenant bien connues : \[\begin{aligned} \overrightarrow{E}&=-\overrightarrow{grad}~V\\ \frac{D_n}{\mu_n}&=\frac{k~T}{e}\quad;\quad\frac{D_p}{\mu_p}=\frac{k~T}{e}\quad\text{(relations d'Einstein)}\\ n~p&=n_i^2 \end{aligned} \qquad[3]\]

On obtient la relation : \[V_0~\approx~\frac{k~T}{e}~\ln\frac{N_d~N_a}{n_i^2}\qquad[4]\]

Habituellement, le dopage est assez abondant pour que : \[(N_d,~N_A\approx 10^3\times n_i)\qquad (\text{Ge~intrinsèque})\]

Ceci donne pour le logarithme népérien \(\ln\) une valeur de l’ordre de 14, donc pour \(V_0\) à la température ordinaire une barrière de 0,36 V.

Voyons comment sont disposés, en régime d’équilibre et circuit ouvert, les différents porteurs de charges.

3.2. Répartition des charges

Supposons une jonction graduelle : les concentrations \(N_a\) et \(N_d\) des atomes (donneurs et accepteurs), passent de presque zéro (présence d’impuretés indésirables) à leur valeur maximale, ceci dans un intervalle de l’ordre du micromètre.

Deux morceaux séparés de Ge P et Ge N sont électriquement neutres et l’on a toujours en chaque élément de volume : \[\begin{aligned} &e(N_a+n)=p~e\quad(\text{ou}~p~\approx~N_a)\\ &e(N_d+p)=n~e\quad(\text{ou}~n~\approx~N_d) \end{aligned} \qquad[5]\]

Il en est encore de même pour deux éléments de volume de la jonction, loin de la jonction. Les atomes donneurs ou accepteurs sont fixés au réseau, presque tous à l’état d’ions, et ils ne diffusent pas.

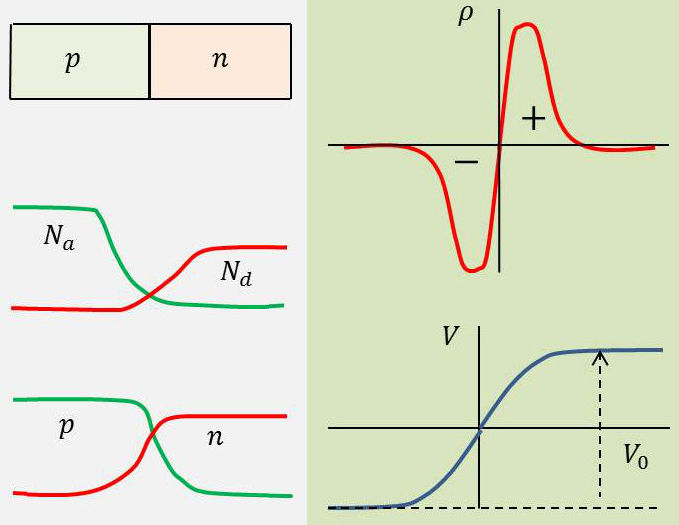
Par contre, près de la jonction, la diffusion des trous [\((p)\rightarrow(n)\)] et la diffusion des électrons de la région [\((n)\rightarrow(p)\)] produisent les phénomènes suivants :

La région P de la diode devient négative près de la jonction : départ de trous vers la droite et arrivée d’électrons provenant par diffusion de la région N.

De même, la région N devient positive près de la jonction : arrivée de trous diffusés de la région P et départ d’électrons diffusés vers la gauche.

Par suite de cette double diffusion électrons-trous, il apparaît une charge d’espace \(\rho\) négative du côté P de la jonction, positive du côté N.

À partir de \(\rho\), l’équation de Poisson : \[\Delta V+\frac{\rho}{\varepsilon}=0\qquad[6]\]

et deux intégrations permettent de retrouver \(V(x)\) et la hauteur de la barrière de potentiel : \[V_0=V(+\infty)-V(-\infty)\]

La région N est devenue positive par rapport à la région P.

4. Jonction PN polarisée en sens direct

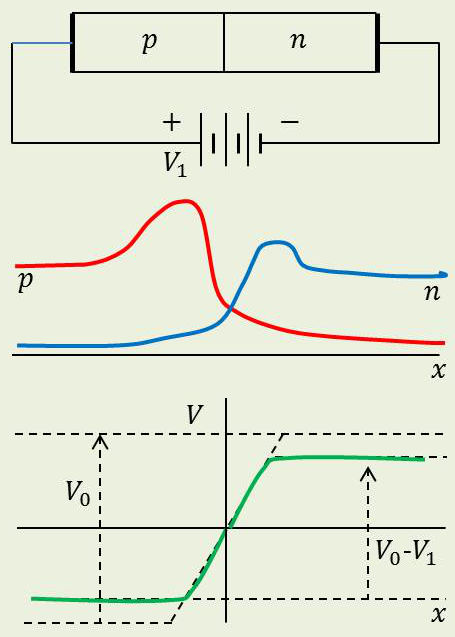
Relions la région P au pôle positif d’une batterie et la région N au pôle négatif, de manière à établir une DDP \(V_1\) entre les deux régions. La barrière de potentiel passe de \(V_0\) à \((V_0-V_1)\).

Le circuit étant fermé, \(V_0\) est automatiquement compensé par les différences de potentiel de contact entre les conducteurs extérieurs, et entre ceux-ci et les régions N et P.

Quand \(V_1\gg V_0\), tout se passe comme si nous avions une f.e.m \(V_1\) en série avec la résistance du circuit extérieur et une faible résistance représentant la diode (fraction d’ohm à quelques ohms), due essentiellement à la résistance entre les contacts soudés et les deux semi-conducteurs.

L’introduction de la batterie \(V_1\) détruit l’équilibre entre les courants de trous vers la droite et vers la gauche que nous avons vu précédemment (de même pour les électrons). La diffusion des trous vers la droite augmente considérablement car ils n’ont plus à franchir qu’une barrière de potentiel (\(V_0-V_1\)) au lieu de \(V_1\). Il en est de même de celle des électrons vers la gauche.

Une fois les trous arrivés en région N, ils se recombinent rapidement aux électrons, de même pour les électrons arrivés en région P.

La somme (\(I_p+I_n\)) des courants transportés par trou et par électron est indépendante de la distance \(x\) à la jonction, mais \(I_p\) décroît avec \(x\) tandis que \(I_n\) croît.

L’ensemble des deux diffusions permet d’obtenir des courants importants dès que \(V_1\approx\) 0,5 V.

5. Injection des porteurs minoritaires

Au voisinage immédiat de la jonction, il y a :

• dans la région N injection de trous provenant de la région P ;

• dans la région P injection d’électrons provenant de la région N.

Dans chaque région, la jonction produit une injection de porteurs minoritaires.

Si nous dopons davantage la région P que la région N (\(N_a~\gg~N_d\)), il y aura beaucoup plus de trous injectés dans la région N que d’électrons injectés dans la région P. Inversement, si c’est la région N la plus dopée (\(N_d~\gg~N_a\)), il y aura beaucoup plus d’électrons injectés dans la région P que de trous dans la région N. On arrive facilement à une valeur 200 pour le rapport injection trous / injection électrons (ou vice versa).

L’emploi d’une jonction PN comme injection de porteurs minoritaires dans une zone de quelques micromètres au delà de la jonction est à la base du fonctionnement des transistors.

6. Jonction PN polarisée en inverse

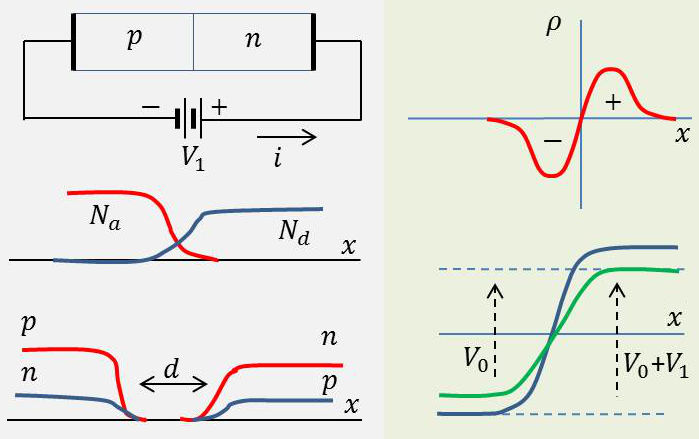
Branchons maintenant le pôle positif de la batterie au semi-conducteur N. On observe un très faible courant \(i\).

La répartition des charges fixes (\(N_a,~N_d\)) des ions, des charges mobiles des trous \(p\) et des électrons \(n\) est figurée ci-contre.

La charge d’espace est : \[\begin{aligned} -(N_a+n-p)~e\qquad(\text{région P})\\ (N_d+p-n)~e\qquad(\text{région N})\end{aligned}\]

On voit qu’il y existe une région de largeur \(d\) vide de toute charge mobile. C’est la zone de déplétion.

À cause de la barrière (\(V_0+V_1\)), les trous de la région P ne peuvent plus diffuser de manière appréciable de gauche à droite, mais il subsiste un très faible courant de trous de droite à gauche, dû aux trous créés par ruptures thermiques de covalences dans la région (N) ainsi qu’un très faible courant d’électrons dû aux électrons de la région (P) aidés à diffuser par (\(V_0+V_1\))

L’ensemble de ces deux courants constitue le courant \(i\), dit courant inverse.

Pratiquement, dès que \(V_1~>\) 0,1 V, le courant \(i\) atteint sa valeur de saturation \(i_s\), indépendante de \(V_1\).

7. Caractéristique d’une diode jonction PN

On peut établir, avec quelques approximations, l’expression du courant \(i\) traversant une diode : \[i=i_0~\Big\{\exp\Big(\frac{e~V_1}{k~T}\Big)-1\Big\}\qquad[7]\]

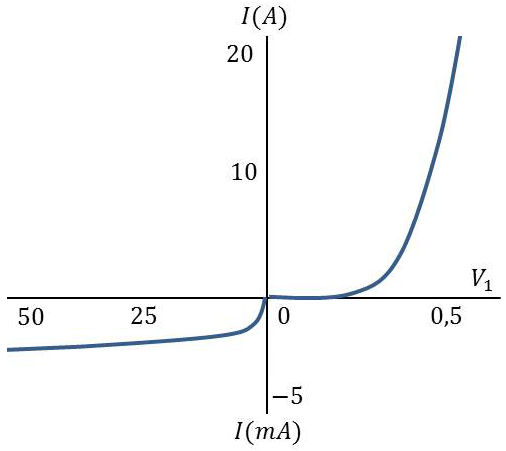
\(V_1\) : DDP établie entre la région P et la région N ( \(V_1>0\) dans le sens direct, \(V_1<0\) dans le sens inverse).

La théorie donne l’expression de \(i_s\) en fonction des coefficients et des longueurs de diffusion des électrons et des trous et de leur concentration loin de la jonction.

Si \(V_1\) est assez négatif (\(i~\approx~-i_s\)), \(i_s\) est proportionnel à \(n_i^2\), donc à \(\exp(-\Delta E/k~T)\). Le courant de saturation augmente donc très vite (en valeur absolue) avec la température.

Le coude de la caractéristique se produit dans un intervalle [+0,05 V ; -0,05 V] environ.

Lorsque \(V_1\) atteint quelques volts, les résistances extérieures commencent à intervenir et donnent des valeurs de \(i\) inférieures à celles prévues par (7).

8. Capacité d’une diode jonction

On sait que dans une diode jonction polarisée en sens inverse, il existe une zone vide de charges libres ou de déplétion séparant les électrons libres de la région N des trous libres de la région P. Par suite, une telle diode se comporte comme un condensateur fictif.

Cette capacité \(C\) de décroît lorsque la polarisation \(V_1\) de la diode devient de plus en plus négative, à la fois parce que la largeur de la zone de déplétion croît et parce que de moins en moins de charges y participent.

Shockley et Schottky ont montré que : \[\begin{aligned} &C=\frac{K}{(V_0-V_1)^{1/2}}\qquad\text{pour une jonction brusque}\\ &C=\frac{K}{(V_0-V_1)^{1/3}}\qquad\text{pour une jonction graduelle} \end{aligned} \qquad[8]\]

Cette capacité est shuntée par une conductance : \[G=\frac{e~i_s}{k~T}~\exp\Big(\frac{e~V}{kT}\Big)\qquad[9]\]

Celle-ci diminue, comme \(C\), quand \(V_1\) devient très négatif.

\(Q=\cfrac{C~\omega}{G}\) facteur de surtension, est maximal pour une valeur peu négative de \(V_1\).

Le schéma équivalent comprend :

• la capacité non linéaire \(C\) shuntée par la conductance non linéaire \(G\) ;

• en série avec une petite résistance \(r\) d’environ 1 \(\Omega\).

Les varicaps ou varactors, sont des diodes jonction à faible capacité (minimum 1 pF) et à capacité (maxima quelques dizaines de pF). Elles fonctionnent comme capacité variable sous l’action d’une tension (\(V_1\)) jusqu’à des fréquences de 3 Ghz (\(\lambda=\) 10 cm) et même 10 Ghz (\(\lambda=3\) cm).

Les principales applications de ces diodes à réactance variable sont :

• les amplificateurs paramétriques ;

• des changeurs de fréquence, à augmentation de fréquence, avec ou sans réaction ;

• des générateurs d’harmoniques et de sous-harmoniques.