1. Dilatation compression des gaz
1.1. Exercice 1
1.1.1. Énoncé
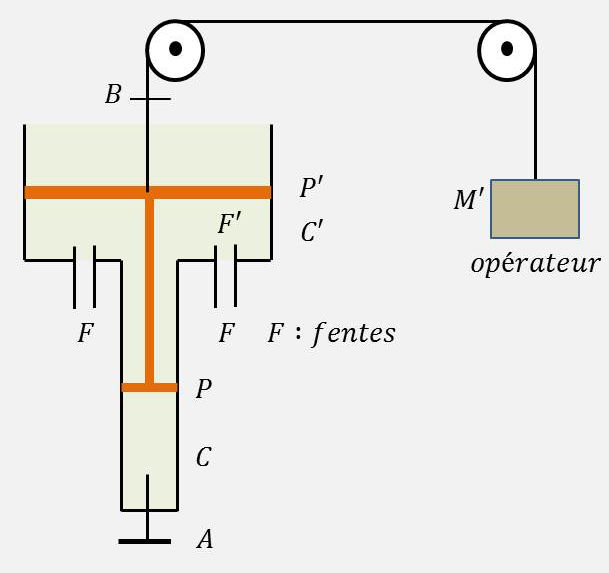 Les deux pistons \(P\) et \(P'\) sont solidaires. Leur ensemble a une masse \(M\) = 49,584 kg. Ils coulissent sans frottement dans les cylindres verticaux \(C\) et \(C'\).
Les deux pistons \(P\) et \(P'\) sont solidaires. Leur ensemble a une masse \(M\) = 49,584 kg. Ils coulissent sans frottement dans les cylindres verticaux \(C\) et \(C'\).
Le cylindre \(C\) a une section \(s\) = 16 cm². Le piston \(P\) et le cylindre \(C\) sont imperméables à la chaleur.
On peut soulever le double piston à l’aide d’une corde enroulée sur deux poulies.
Le robinet \(A\) sert à emprisonner dans le cylindre \(C\) un certain volume d’air sec \(v=s~l_0\), pris dans l’atmosphère extérieure.
L’air est assimilé à un gaz parfait et les conditions extérieures sont : \(t_0\) = 27 °C ; \(P_0\) = 1 atm.
-
Comment peut-on réaliser expérimentalement cette compression ? Quelle est la pression finale \(P_1\) obtenue lorsque le piston appuie sur le gaz de tout son poids ?
-
Calculer la température finale \(T_1\). Sachant que \(l_0\) = 100 cm, calculer la longueur \(l_1\) de la colonne gazeuse.
-
Quels sont en joules les travaux ?
-
\(W_q\) : reçu par le gaz
-
\(W_p\) : fourni par la chute du piston
-
\(W_a\) : fourni par l’atmosphère
-
\(W_{op}\) : reçu par l’opérateur qui agit sur la corde
1.1.2. Solution
1) Pour réaliser la compression adiabatique d’une façon irréversible, il suffit de diminuer très progressivement la masse \(M'\) (manipulée par l’opérateur) dont la valeur passe de \(M=M'\) à la valeur \(M'=0\)
Lorsque le piston appuie de tout son poids sur l’air emprisonné dans le cylindre, il exerce une pression \[\Delta P=\frac{P}{s}=\frac{49,584}{16}=3,099~\rm kg/cm^2\approx~3~atm\]
Pour mémoire : 1 atm(osphère) \(\approx 1,013\times 10^5~\rm Pa\).
Le gaz est donc à la pression \(P=4~\rm atm\).
On peut dire encore, à \(\varepsilon\) près, que : \[P=P_0+\frac{(M-M')~g}{s}\]
2) Dans la transformation isentropique d’un gaz parfait (hypothèse pour l’air, on a (3 écritures équivalentes) : \[P~V^{\gamma}=\text{cte}\quad;\quad T~V^{\gamma-1}=\text{cte}\quad;\quad T^{\gamma}~P^{1-\gamma}=\text{cte}\]
Pour l’air qui est un gaz diatomique, \(\gamma=7/5\).
État initial : \[P_0\quad;\quad V_0=s~l_0=1,6~l~~~;~~~T_0=300~\rm K\]
État final : \[P_1=4~P_0\quad;\quad V_1=s~l_1~~~;~~~T_1\]
Calcul de la température : \[T_1=T_0~\Big(\frac{P_1}{P_0}\Big)^{(\gamma-1)/\gamma}\]
Calcul du volume (ou équivalents hauteur) : \[l_1=l_0~\Big(\frac{P_0}{P_1}\Big)^{1/\gamma}\]
Applications numériques : \[\begin{aligned} T_1&=445~{\rm K}\quad;\quad t_1=172,8~^o\rm C \\ l_1&=37,15~{\rm cm}\quad\rightarrow\quad V_1\approx 0,6~\rm L~(valeur~exacte~:~0,594~L) \end{aligned}\]
3) Rappelons l’expression du travail reçu par le gaz (cours) : \[W_q=\frac{\Delta (P~v)}{\gamma-1}=\frac{(P_i~v_i)-(P_f~v_f)}{\gamma-1}\]
\(P\) exprimé en pascals et \(v\) exprimé en m³ (système d’unités SI) : \[W_q=202,6~\rm J\]
Le piston descend de : \[l_0-l_1=100-37,15=62,85~\rm cm\]
Il fournit un travail de : \[W_p=M~g~(l_0-l_1)=\frac{M~g}{s}~s~(l_0-l_1)\]
On a vu que : \[\frac{Mg}{s}\approx~3~\rm atm=3~(1,013\times 10^5)~Pa\]
On note que : \[s~(l_0-l_1)=1~\rm L=10^{-3}~m^3\]
Tous calculs faits : \[W_p=303,9~\rm J\]
Quant au travail fourni par l’atmosphère, il suffit de considérer le déplacement du piston vu de la partie supérieure (à la pression atmosphérique) qui descend également de 100 cm (équivalent volume 1 L)comme dans le cas précédent, cette pression atmosphérique étant constante.
On a donc : \[W_a=103,3~\rm J\]
L’opérateur qui agit sur la ficelle reçoit un travail : \[W_{op}=W_p+W_a-W_q=202,6~\rm J\]
2. Équation d’état
2.1. Exercice 1
2.1.1. Énoncé
Un gaz obéit à l’équation : \[P=\frac{R~T}{V}~\Big\{1+\frac{A(t)}{V}\Big\}\quad\qquad A~\text{fonction de }T\]
Trouver l’équation différentielle des adiabatiques pour ce gaz.
2.1.2. Solution
Relation aux coefficients thermodynamiques {\(\lambda,~\mu,~C,~c,~h,~l\)} : \[dQ=C~dT+h~dP=c~dT+l~dV=\lambda~dP+\mu~dV\]
À pression constante (\(dP=0\)) : \[C~dT=\mu~dV~~~~\Rightarrow~~~~dQ_p~:~\mu=C~(\frac{\partial T}{\partial V})_P~~~~~~(\text{sous-entendu}~~P=cte)\]
À volume constant (\(dV=0\)) : \[c~dT=\lambda~dP\quad\Rightarrow\quad dQ_v~:~~\lambda=c~\Big(\frac{\partial T}{\partial P}\Big)_V\qquad(\text{sous-entendu :}~~V=cte)\]
En régime adiabatique (\(dQ=0\)), on peut écrire : \[0=\lambda~dP+\mu ~V=C~\Big(\frac{\partial T}{\partial V}\Big)~dV+c~\Big(\frac{\partial T}{\partial P}\Big)~dP\]
Ou encore : \[\gamma~\frac{\partial T}{\partial V}~dV+\frac{\partial T}{\partial P}~dP=0\qquad\text{avec :}\quad\gamma=\frac{C}{c}\]
Pour un gaz parfait, on aurait (\(P~v=r~T\)) : \[\gamma~\frac{P}{r}~dV+\frac{V}{r}~dP=0\quad\Rightarrow\quad P~V^{\gamma}=cte\]
Avec un gaz réel d’équation caractéristique : \[P=\frac{r~T}{V}~\Big(1+\frac{a}{V}\Big)=\frac{r~T}{V^2}~(V+a)\]
Pour \(T=cte\), on a (dérivation logarithmique) : \[\Big(\frac{dP}{P}=-\frac{2dV}{V}+\frac{dV}{V+a}\Big)_T\quad\Rightarrow\quad\Big(\frac{\partial P}{\partial V}\Big)_T=-P~\Big(\frac{2}{V}-\frac{1}{V+a}\Big)\]
Reprenons une expression précédente sous une autre forme : \[\gamma~\frac{\partial T}{\partial V}~dV+\frac{\partial T}{\partial P}~dP=\gamma~\Big(\frac{\partial T}{\partial P}~\frac{\partial P}{\partial V}\Big)~dV+\frac{\partial T}{\partial P}~dP=0\]
Il vient : \[\gamma~P~\Big(\frac{2}{V}-\frac{1}{V+a}\Big)~dV+dP=0\]
Ou encore : \[\gamma~P~\frac{V+2a}{V+a}~dV+V~dP=0\]
Remarque
Quand \(a\rightarrow 0\) ou quand \(V\rightarrow\infty\), on retrouve les formules du gaz parfait.

