1. Polarisation rectiligne
1.1. Exercice 1
1.1.1. Énoncé
 Polarisation par réflexion
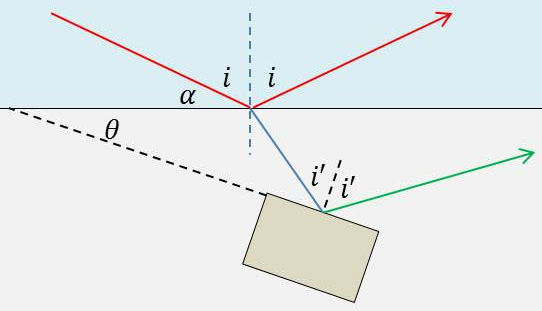
Polarisation par réflexion
-
Quelle doit être la hauteur angulaire du Soleil au-dessus de l’horizon pour que la lumière réfléchie par une nappe d’eau calme soit complètement polarisée (indice de l’eau \(n\) = 4/3 ?
-
Lorsque le Soleil atteint cette hauteur, on immerge dans une cuve d’eau un bloc de verre, d’indice \(N\) = 1,6, dont la surface plane fait l’angle \(\theta\) avec l’horizontale.
Déterminer \(\theta\) pour que le faisceau réfléchi par le bloc soit lui aussi complètement polarisé. Ce faisceau émerge-t-il ?
1.1.2. Solution
1) Les rayons doivent tomber sur la surface de l’eau sous l’incidence brewstérienne. Les rayons réfléchis et réfractés sont alors perpendiculaires : \[i=\frac{\pi}{2}-r\quad\Rightarrow\quad\sin i=\cos r=n~\sin r\]
D’où : \[\tan~r=\frac{1}{n}=\frac{3}{4}\]
Et la hauteur du Soleil : \[\alpha=\frac{\pi}{2}-i=r=\arctan(3/4)\quad\Rightarrow\quad\alpha\approx 37~^o\]
2) Avec le bloc de verre, on aura : \[\tan~i=n'=\frac{N}{n}\quad\Rightarrow\quad i'=\arctan n'=\arctan 1,2\approx~50,2~^o\]
On a alors : \[i'=r+\theta\quad\Rightarrow\quad\theta\approx~13,2~^o\]
Si le bloc de verre était horizontal, le rayon réfléchi atteindrait la surface de l’eau sous une incidence \(r\). Comme il fait l’angle \(\theta\) avec l’horizontale, l’incidence du faisceau réfléchi est : \[r+2~\theta=63,4~^o\]
L’angle de réflexion limite à la surface de l’eau est donnée par : \[\sin\lambda=\frac{1}{n}=0,75\quad\Rightarrow\quad\lambda\approx~48,5~^o\]
Le deuxième faisceau polarisé, d’incidence supérieure à l’angle de réfraction limite \(\lambda\) est totalement réfléchi par la surface de l’eau.
1.2. Exercice 2
1.2.1. Énoncé
La fente source \(F\) d’un appareil à fentes de Young est éclairé en lumière monochromatique, de longueur d’onde \(\lambda=0.6\mu\), polarisée rectiligne par une lame polaroïde \(P\).
Les fentes de Young \(F_1\) et \(F_2\), équidistantes de \(F\) et distantes de \(a\) = 1 mm, sont disposées à \(D\) = 4 m de l’écran d’observation (E).
On couvre \(F_1\) et \(F_2\) de deux lames polaroïdes identiques \(P_1\) et \(P_2\).
Qu’observe-t-on sur l’écran lorsque :
-
les axes de \(P_1\) et \(P_2\) sont parallèles et à 45 ° de l’axe de \(P\) ?
-
les axes de \(P_1\) et \(P_2\) sont perpendiculaires et à 45 ° de l’axe de \(P\) ?
1.2.2. Solution
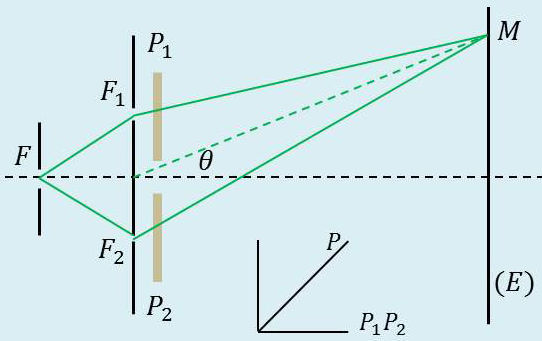 1) Axes de \(P_1\) et \(P_2\) parallèles
1) Axes de \(P_1\) et \(P_2\) parallèles
En \(M\) interfèrent les deux vibrations rectilignes, parallèles, de même amplitude \(A\) issues de \(F_1\) et \(F_2\).
Le calcul est celui des franges de Young.
Déphasage des deux vibrations : \[\varphi=\frac{2\pi}{\lambda}~\delta=\frac{2\pi}{\lambda}~\frac{a~y}{D}\]
Composition des deux vibrations : \[a~\cos(\omega~t)+a~\cos(\omega~t-\varphi)\]
Application de la formule : \[\cos~p+\cos p=2~\cos\frac{p+q}{2}~\cos\frac{p-q}{2}\]
Expression de la vibration résultante : \[s(t)=2~a~\cos\frac{\varphi}{2}~\cos\Big(\omega~t-\frac{\varphi}{2}\Big)\]
Intensité résultante : \[I=4~a^2~\cos^2\frac{\varphi}{2}\]
Interfrange : \[I=\frac{\lambda~D}{a}=2,4~\rm mm\]
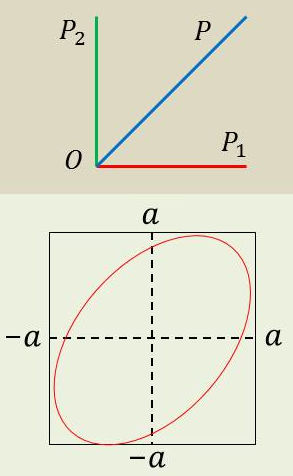 2) Axes de \(P_1\) et \(P_2\) perpendiculaires, à 45 ° de l’axe de \(P\)
2) Axes de \(P_1\) et \(P_2\) perpendiculaires, à 45 ° de l’axe de \(P\)
En \(M\) se composent cette fois deux vibrations rectilignes perpendiculaires, de même amplitude \(a\) et déphasées de \(\varphi\).
La vibration résultante est elliptique, l’ellipse étant inscrite dans un carré de côté \(2~a\) et dont la forme, fonction de \(\varphi\), varie avec la position du point \(M\).
Mais cette fois, l’intensité de dépend pas de \(\varphi\) et elle est égale à la somme des intensités des deux vibrations des intensités rectilignes composantes : \[I=2~a^2=cte\]
L’éclairement de l’écran est donc uniforme : les franges d’interférences ont donc disparu.

